5.2. Правила кристаллографической установки кристаллов для различных сингоний.

Классы симметрии с единым координатным репером объединяются в семейство, называемое сингонией, или системой.

Рассмотрим разбиение 32 классов симметрии на кристаллографиче­ские сингонии в трех категориях: низшей, средней и высшей.

Низшая категория (а Ь с)

И з условия неэквивалентности координатных направлений следует, что к низшей категории могут относиться только классы, не имеющие осей высшего порядка. В противном случае появились бы эквивалентные направления. Следовательно, элементами симметрии этих классов могут быть только оси симметрии 2-го порядка: поворотные —L₂, инверсион­ные —L_i2 = Р. или зеркально-поворотные L₂ = С.

Число особых направлений в кристалле, как видно из теорем взаи­модействия элементов симметрии, может быть равно 3, 1 или 0. Случая с двумя особыми направлениями быть не может, так как автоматически появится третье — результирующее.

Если в кристалле присутствуют три особых направления (а ими в кри­сталлах низшей категории могут быть лишь поворотные или инверсион­ные оси 2-го порядка), то между координатными направлениями неиз­бежны прямые углы. Если же угол между какими-либо осями окажется отличным от 90°, то возникнет ось высшего порядка, что приведет к появлению эквивалент­ных координатных направлений, а значит к другой координатной сис­теме и, соответственно, к иной категории. Следовательно, при наличии трех особых направлений, но которым выбираются оси направления, ко­ординатный репер будет прямоугольным, т.е. ,

Сингонию с таким репером называют ромбической. Ось Z во всех классах ромбической сингонии принято совмещать с поворотной осью симметрии L₂.

Точечная симметрия ромбических кристаллов описывается следу­ющими группами: 3L₂, L₂2P, 3L₂3PC (рис.5.6).

в

Рис. 5.6 Кристаллы минералов ромбической сингонии классов: а — L₂2Р (каламина= гемиморфита — Zn₄ [SiO₂](ОН)₂ Н₂О), б— 3L, (эпсомита - Мg[SO₄]7Н₂O), в – 3L₂3PC (серы - 5)

Е сли в кристалле присутствует одно особое направление, то оно мо­жет быть представлено либо поворотной осью 2-го порядка (L₂), либо ин­версионной осью L₂, совпадающей с нормалью к плоскости симметрии L₂=Р, либо и тем и другим, когда плоскость симметрии оказывается перпендикулярной к оси L₂ (т.е. когда нормаль к плоскости L₂ с поворотной осью L₂). В этом случае с единственным направлением совмещают одну из координатных осей, две другие условно выбирают в плоскости, перпендикулярной этому особому направлению, по возмож­ным или действительным ребрам кристалла. В результате приходим к координатному реперу с двумя прямыми и одним косым, отличающимся от 90°, углом (углом между координатными осями, выбранными парал­лельно ребрам кристалла). Отсюда и название сингонии — моноклинная— с координатной системой а b с, и углом , называемым углом моно­клинности.

С уществуют две установки моноклинных кристаллов: минералоги­ческая (классическая), когда с единственным особым направлением со­вмещают координатную ось y (угол моноклинности в случае будет ), и рациональная (кристаллографическая), когда с особым направ­лением совмещают ось z (угол моноклинности ). Таким образом, задание угла моноклинности ( или ) указывает на установку кристалла.

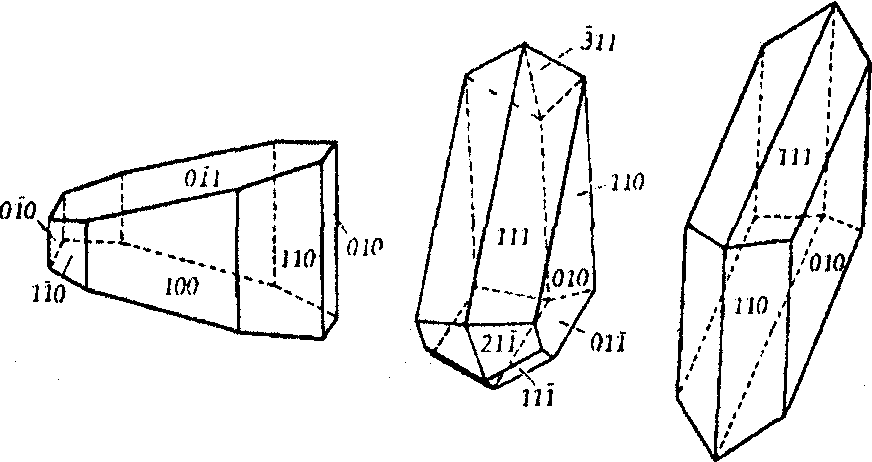
К моноклинной системе (сингонии) относятся следующие точечные группы: L₂P, L₂PC (рис. 5.7).

а б в

Рис.5.7 Кристаллы моноклинной сингонии классов: а — L₂ (лактозы — молочного сахара),б –P (хильгардита – Са₂ [В₅О₈ (OН)₂CI], в – L₂ РС (гипса - Са[SO₄ ] • 2НO)

П ри отсутствии в кристаллах особых направлений (т.е. либо в кри­сталле вообще нет элементов симметрии, либо есть только центр ин­версии — L₂= С) координатные оси выбирают по действительным или возможным ребрам кристалла, что приводит к координатному реперу самого общего вида:

,

Название сингонии с такой косоугольной координатной системой — триклинная.

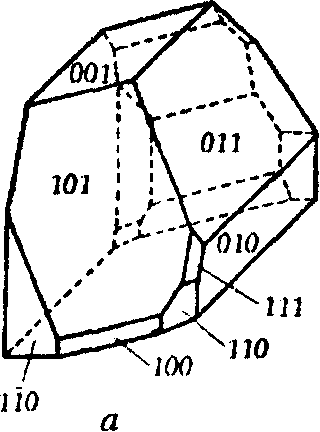
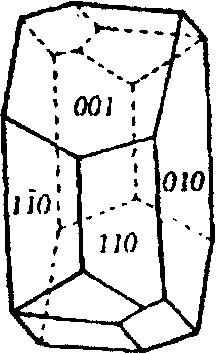
Симметрия триклинных кристаллов описывается двумя точечными группами — L₁ и С (рис.5.8).

б

Рис. 5.8. Кристаллы триклиной сингонии класссов: а — L₁ (серноватистокислого кальция — СаS₂O₃ 6Н₂О), б— С (анортита — Са[AI₂Si₂ O₈]

Средняя категория (а = b с)

Из условия эквивалентности двух горизонтальных координатных на­правлений (а = b) следует, что симметрия кристаллов средней категории описывается группами с единственной осью L_n высшего порядка: 3, 4, 6, . С этой осью совмещают вертикальную координатную ось z, а две другие — x и y— выбирают в плоскости, перпендикулярной главной оси, по осям 2-го порядка — поворотным (L₂) или инверсионным (L₂=Р) — нормалям к плоскостям симметрии. Если же горизонтальных особых на­правлений в кристалле нет, то координатные оси выбирают по ребрам (возможным или действительным). Отсюда и углы между главной осью L_n (осью z) и горизонтальными осями x и y прямые, т.е. .

Угол между осями x и y определяется порядком главной оси и ра­вен 90° в случае присутствия оси 4-го порядка и 120° — осей 3-го и 6-го порядков. Поэтому в средней категории выделяются две координатные системы, которым соответствуют две сингонии:

- тетрагональная — а = b с, , к которой относятся точечные группы: L₄, L₄, L₄PC, L₄4L₂, L₄4P, L₄2L₂2P, L₄4L₂5PC (рис.5.9 )

По традиции в качестве координатных горизонтальных осей в клас­сах тетрагональной сингонии предпочитают выбирать оси L₂, в классах гексагональной сингонии — нормали к плоскостям симметрии — Р = L_2i

Особенность симметрии гексагональных кристаллов состоит в нали­чии трех горизонтальных эквивалентных особых направлений и, следо­вательно, трех координатных осей — x, y и u, расположенных под углом 120° одна к другой. классу относятся кристаллы -кварца), ж — L₆РС (апатита — Са₅(РО₄)₃F).

Е сли в основу распределения классов симметрии по сингониям за­ложена единая координатная система, то в средней категории выделяют две сингонии: тетрагональную и гексагональную, координатные системы которых обслуживают кристаллы с осями 4-го, 3-го и 6-го порядков со­ответственно. Если же в основу выделения сингонии положить порядок главной оси, то формально можно выделить тригоналъную сингонию с осями 3-го порядка.

г д е ж

Рис. 5.9. Кристаллы тетрагональной сингонии классов: а — L₄ (вульфенита РЬМоО₄ ), б – L₄ (канита Са₄BАs₂О₁₂ 4Н₂0), B – L₄2L₂2Р (халькопирита СuFeS₂), г – L₄4L₂ (метил-аммониевого иодида NH3(СНз)I), д – L₄РС (шеелита СаWО₄ ), е – L₄4Р (гидрата фтористого серебра АgF H₂О), ж — L₄4L₂5РС (циркона ZrSiO₄)

- гексагональная – а =b c, , , объединяющая классы симметрии с осями 3-го и 6-го порядков:

L ₃,L₃=L₃c, L₃3L₂, L₃3P, L₃3L₃3P (рис.5.10 ) и L₆, L₆=L₃P, L₆PC, L₆6P, L₆3L₂3P, L₆6L₂7PC (рис.5.11)

а б в г д

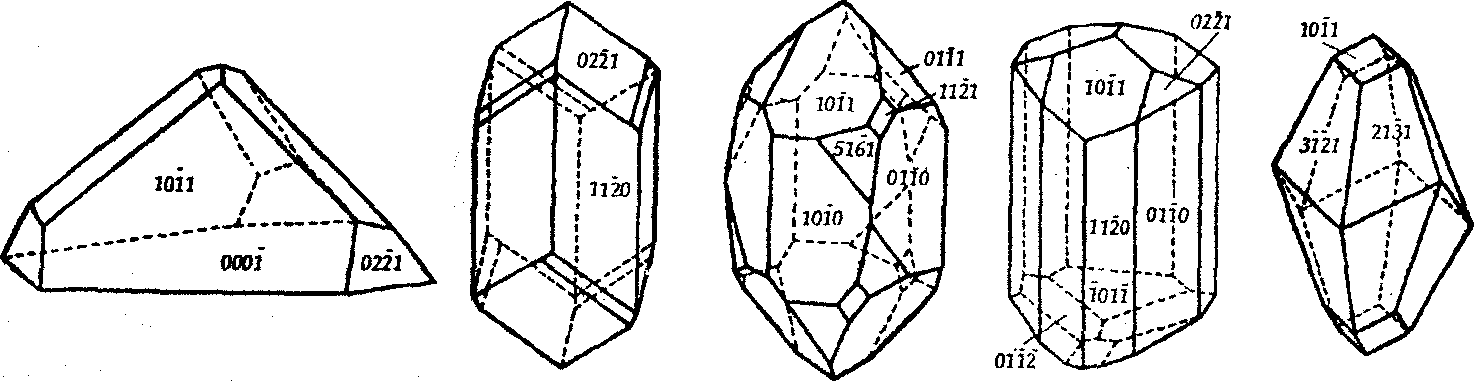
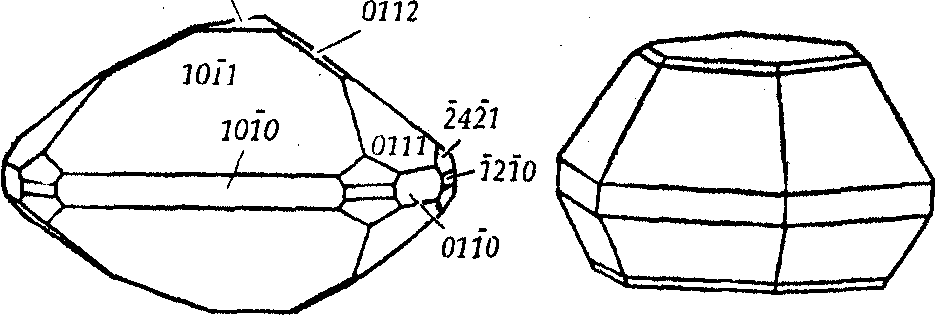
Рис. 5.10. Кристаллы минералов тригональной подсингонии гексагональной сингонии классов:

а — L₃ (шестиводного периодата натрия Na₂I₂O₈ 6Н₂О), б – L₃С = L₃ (диоптаза – Сu₆ [Si₆O₁₈]•6Н₂O), в – L₃3L₂ (кварца -SiO₂), г – L₃ЗР (турмалина – Na(Ca)Mg₃AI₆B₃[Si₆O₁₈](O,OH)₁₂), d – L₃3L₂3PC (кальцита – CaCO₃).

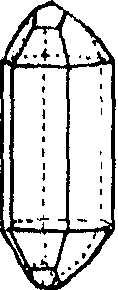
а б в

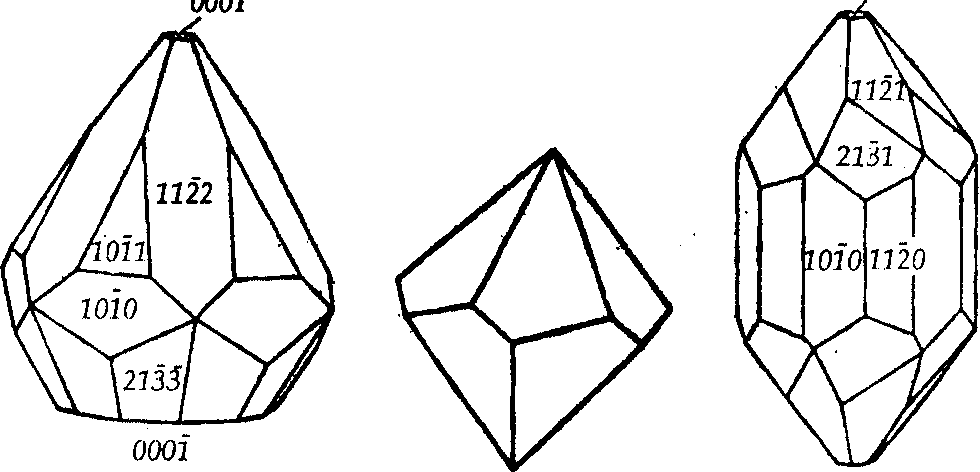
г д е

Р ис.5.11. Кристаллы собственно гексагональной сннгонии классов: а — L₃3L₂4Р (бенитоита — ВаТi[Si₃O₉]), б — L₆ (нефелина — NаАISiO₄), B — L₆=L₃Р (кислого фосфата серебра Ag₂ (РО₄)Н), д – L₆6 Р (цинкита -Zn0), е — L₆6L₂ (гексагональный трапецоэдр, к этому)

Однако, поскольку и в тригональных, и в гекса­гональных кристаллах сходны простые формы (гексагональные при­змы и пирамиды встречаются в присутствии осей и 3-го, и 6-го порядков соответственно. Если же в основу выделения сингоний положить порядок главной оси, то формально можно выделить тригональную сингонию с осями 3-го порядка. Однако, поскольку и в тригональных, и в гексагональных кристаллах сходны простые формы (гексагональные призмы и пирамиды встречаются в присутствии осей и 3-го, и 6-го порядков) и однотипная примитивная решетка Бравэ (Р)объединяет все 12 гексагональных классов с осями 3-го и 6-го порядков, нет смысла дробить эти классы на две сингонии. Присутствие же в кристаллах осей 3-го порядка можно подчеркнуть выделением в гексагональной сингонии, объединяющей классы с осями 3-го и 6-го порядков, тригональной подсингонии, выделяющей классы только с осями 3-го порядка. Искусственность разбиения, указанных классов симметрии на две разные сингонии проявляется еще и в том, что L₃C=L₃ не что иное, как L₆, a L₃P = L₃ – L₆.

Высшая категория (а = b = с)

Если предположить косоугольную координатную систему с углами , то эквивалентность координатных направлений можно объяснить присутствием в кристалле лишь одной оси 3-го порядка, равнонаклонной к выбранным координатным направлениям. А это отсыла­ет нас к устаревшей (миллеровской) установке тригонального кристалла с координатными осями, направленными не по особым направлениям кристалла (рис.5.12, a), а по трем его ребрам, образующим одинаковые углы с единственной осью L₃ отличающиеся от 90° (рис.5.12, б).

Рис.5.12 Различные способы координатных осей в кристаллах гексагональной сингонии: а – кристаллографическая установка; б – установка Миллера.

Е сли же координатная система прямоугольна ( ), то наличие равнонаклонных к осям L₃ трех осей — 3L_4, 3L₄ или 3L₂ — по­зволяет по ним выбрать в кристалле три взаимно перпендикулярных координатных направления x, y и z (рис.5.13). В результате имеем прямоугольную систему координат с эквивалентными координатными осями, где через каждую пару противоположных октантов пройдут оси 3-го порядка — 4L₃, равнонаклонные к координатным направлениям.

Таким образом, к высшей категории относится лишь одна сингония (система) — кубическая: , объединяющая точечные группы:

3L₄4L₃6L₂9PC, 3L₄4L₃6L₂, 3L₂4L₃3PC, 3L₄4L₃6P, 3L₂4L₃ (рис.5.13).

а б в г д

Р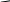 ис. 5.13. Кристаллы минералов кубической сингонии классов: 1 — 3L₂4L₃ (хлората натрия – NaCIO₃), 2– ЗL₄4L₃6L₂ (куприта – Сu₂O), 3 – ЗL₂4L₃ЗРС (пирита – FeS₂), 4 – 3L₄4L₃6P (тетраэдрита – Сu₃SbS_3-4), 5 -3L₄4L₃6L₂ 9РС (граната – Са₃AI₂ [SiO₄]₃).

Итак, если группы симметрии разделить по сингониям в соответ­ствии с координатными системами, естественно выделять шесть синго­нии (табл. 5.1).

Таблица 5.1

Характеристики координатных систем шести сингонии в трех

кристаллографических категориях

Категория	Степень эквивалентности координатных направлений	Угловые характеристики координатных систем	Сингонии
Низшая			Триклинная
		,	Моноклинная
			Ромбическая
Средняя			Тетрагональная
			Гексагональная
Высшая			Кубическая