
- •Основы кристаллографии и дефекты кристаллического строения
- •Лекция 1. Основные понятия о кристаллах План лекции
- •1.1. Закон постоянства гранных углов
- •Контрольные вопросы
- •Лекция 2. Структура кристаллов и пространственная
- •План лекции
- •2.1. Элементарная ячейка, её выбор, метрика
- •2.2. Кристаллическая структура
- •2.3. Кристаллографические символы узлов, плоскостей и направлений в кристаллах кубической сингонии
- •2.4. Символы узлов
- •2.5. Символы рядов (ребер, направлений)
- •2.6. Символы плоскостей (граней)
- •Контрольные вопросы
- •3.2. Определение символа атомной плоскости по координатам трёх узлов пространственной решётки
- •3.4. Кристаллографическая символика в гексагональной сингонии
- •Контрольные вопросы
- •Лекция 4. Элементы симметрии конечных фигур План лекции
- •4.1. Понятие о симметрии
- •4.2. Элементы симметрии кристаллических многогранников
- •Обозначение элементов симметрии
- •4.3. Взаимодействие симметрических операций (элементов симметрии)
- •4.4. Осевая теорема Эйлера
- •4.5. Теоремы сложения элементов симметрии
- •4.6. Точечные группы симметрии
- •Контрольные вопросы
- •5.2. Правила кристаллографической установки кристаллов для различных сингоний.
- •5.3. Кристаллографические проекции
- •5.4. Сферическая проекция
- •5.5. Стереографическая проекция
- •5.6. Гномостереографическая проекция
- •Контрольные вопросы
- •План лекции
- •6.1. Классы симметрии
- •6.2. Виды симметрии кристаллов, обладающих единичных направлением
- •6.3. Элементы симметрии бесконечных фигур
- •6.4. Винтовые оси симметрии
- •6.5. Плоскость скользящего отражения
- •6.6 Решетки Бравэ
- •6.7. Условия выбора ячеек Бравэ
- •6.8 Характеристика решеток Бравэ
- •Тип ячейки Бравэ.
- •6.9. Трансляционная группа, базис ячейки
- •6.10. Пример Выбора элементарной ячейки Бравэ
- •Контрольные вопросы
- •Лекция 7. Задачи, решаемые кристаллохимией План лекции
- •7.1 Координационное число, координационный полиэдр, число формульных единиц
- •7. 2. Плотнейшие шаровые упаковки в кристаллах
- •7.3. Основные типы структур
- •7.4. Основные категории кристаллохимии
- •Контрольные вопросы
- •Лекция 8. Точечные дефекты План лекции
- •8.1. Понятие об идеальном и реальном кристалле
- •8.2. Классификация дефектов кристаллической решетки
- •8.3. Точечные дефекты
- •8.4. Искажение решетки вокруг точечных дефектов
- •8.5. Термодинамика точечных дефектов
- •8.6. Миграция точечных дефектов
- •8.6.1.Миграция вакансий
- •8.6.2. Миграция межузельных атомов
- •8.6.3.Миграция примесных атомов
- •Контрольные вопросы
- •Лекция 9. Основные типы дислокаций и их движение План лекции
- •9.2. Скольжение краевой дислокации
- •9.3.Переползание краевой дислокации
- •9.6. Смешанные дислокации и их движение
- •Контрольные вопросы
- •Лекция 10. Количественные характеристики дислокаций План лекции
- •10.2 Вектор Бюргерса
- •10.3. Плотность дислокаций
- •Контрольные вопросы
- •Лекция 11. Упругие свойства дислокаций План лекции
- •11.1. Энергия дислокации
- •11.2. Силы, действующие на дислокацию
- •11.3. Упругое взаимодействие параллельных краевых дислокаций
- •11.4. Упругое взаимодействие параллельных винтовых дислокации
- •Контрольные вопросы
- •Лекция 13. Пересечение дислокаций План лекции
- •13.1. Пересечение краевых дислокаций
- •13.2. Пересечение краевой и винтовой дислокаций
- •13.3. Пересечение винтовых дислокаций
- •13.4. Движение дислокации с порогами
- •13.5. Пересечение растянутых дислокаций
- •Контрольные вопросы
- •14.1.2 Атмосферы Снука
- •14.1.3. Атмосферы Сузуки
- •1.4.2. Взаимодействие дислокаций с вакансиями и межузельными атомами
- •Контрольные вопросы
- •Лекция 15. Образование дислокаций План лекции
- •15.1. Происхождение дислокаций
- •15.2. Размножение дислокаций при пластической деформации Источник Франка — Рида
- •Контрольные вопросы
- •Лекция 16. Границы зерен и субзерен План лекции
- •16.1.Границы кручения и наклона
- •16.2. Малоугловые границы
- •16.3. Высокоугловые границы
- •16.4. Специальные и произвольные границы
- •16.5. Зернограничные дислокации
- •План лекции
- •17.2. Торможение дислокаций при их взаимодействии с другими дислокациями и границами зерен
- •17.3. Торможение дислокаций дисперсными частицами
- •17.4. Выгибание дислокаций между дисперсными частицами
- •17.5. Локальное поперечное скольжение
- •17.6. Перерезание дислокациями дисперсных частиц
- •17.7.2. Торможение дислокаций в твердых растворах
4.6. Точечные группы симметрии
Полное сочетание элементов симметрии кристаллического многогранника называется его классом симметрии, или точечной группой симметрии.
Понятие класса симметрии кристалла эквивалентно понятию точечной группы симметрии. Понятие группы дается следующим образом.
Множество различных а,b,с… составляет математическую группу, если оно удовлетворяет следующим условиям.
1) Произведение любых двух элементов или квадрат какого- либо элемента множества принадлежит тому же множеству.
2) Для любых трех элементов множества выполняется ассоциативный (сочетательный) a(bc)=(ab)c;
3) В множестве существует единичный (нейтральный) элемент e такой что ае=еа=а;
4) Для любого элемента a существует элемент a-1, принадлежащий тому же множеству, так что aa-1=a-1a=e
Всем этим условиям удовлетворяет любой из 32 классов симметрии.
Единичное направление. Плоскости симметрии, оси симметрии простые и инверсионные, центр симметрии обнаруживается в кристаллах в различных сочетаниях. Например, обычная поваренная соль(хлористый натрий) кристаллизуется в форме кубов, алмаз, квасцы- в форме октаэдров (восьмиугольников). Полный набор элементов симметрии у этих разных многогранников один и тот же: девять плоскостей m(p) – три координатные и шесть диагональных), три оси 4(L4), четыре оси 3 (L3), шесть осей 2(L2) и центр симметрии -1 (с). В звездочках снежинок или иголочках инея, как в шестигранном карандаше, отчетливо проявляется иная симметрия, в которой ось симметрии 6 (L6) является единственной и ее нельзя повторить никакими другими операциями симметрии, свойственными этим кристаллам. Единственное , не повторяющееся в многограннике направление называется особым или единичным. Единичным направлением является ось 6 в шестигранной призме или пирамиде. Но ось 4 в кубе и октаэдре – уже не единичная. Этих осей здесь 3, и каждая из них может совместиться с другой такой же осью, например путем отражения в плоскости симметрии. В кубе и октаэдре вообще нет единичных направлений, для любого направления в них можно найти симметрично эквивалентные направления.
Контрольные вопросы
1. Укажите, что называют элементами симметрии.
2. Объясните, что такое симметрия.
3. Назовите элементы симметрии.
4. Дайте определение центра инверсии.
5. Дайте определение оси симметрии.
6. Дайте определение плоскости симметрии.
7. Объясните, что такое инверсионная ось симметрии.
Лекция 5. Кристаллографические категории и сингонии. Кристаллографические проекции
План лекции
1. Соотношение между периодами и осевыми углами в кристаллах разных сингоний.
2. Правила кристаллографической установки кристаллов для различных сингоний.
3. Кристаллографические проекции.
4. Прямой комплекс, обратный комплекс.
5. Сферическая проекция.
6. Стереографическая проекция.
7. Гномостереографическая проекция.
5.1. Соотношение между периодами и осевыми углами в
кристаллах разных сингоний
Пространственная решетка – своеобразный элемент симметрии, задающий и осуществляющий повторяемость эквивалентных точек кристаллического пространства (в физическом и в геометрическом смысле) в трех некомпланарных направлениях. Решетка как бы управляет расположением атомов в кристалле и является тем главным элементом симметрии, без которого нельзя представить строение ни одного кристалла.
Решетке подчиняется всякий бесконечный закономерный узор — одномерный, двухмерный, трехмерный. В структуре кристалла бесконечное число атомов располагается прямолинейными параллельными рядами, в которых (см. рис.5.1) легко прослеживается линейная закономерная повторяемость. Обязательной операцией в регулярной бесконечной одномерной постройке служит перенос — трансляция.

Рис.5.1. Узловой ряд
Каждая точка узора при этом преобразовании повторяется в эквивалентных позициях бесчисленное количество раз. Такую же повторяемость можно увидеть и в одномерном узоре — орнаменте (рис.5.2).

Рис. 5.2. Одномерный бесконечный узор — орнамент
Совмещение
орнамента с самим собой происходит при
переносе – трансляции – этого узора
вдоль определенного направления на
величину трансляционного вектора
![]() .
Одномерной «решеткой» такого узора
служит узловой
ряд — ряд
эквивалентных точек, связанных
операцией переноса (рис.5.1). При этом не
обязательно, чтобы в узле такого ряда
находился атом. В качестве исходной
можно взять любую точку одномерного
пространства. Тогда в узлах ряда окажутся
точки, во всех отношениях эквивалентные
исходной. Перемещение фигур при этом
может происходить в прямом и обратном
направлениях.
.
Одномерной «решеткой» такого узора
служит узловой
ряд — ряд
эквивалентных точек, связанных
операцией переноса (рис.5.1). При этом не
обязательно, чтобы в узле такого ряда
находился атом. В качестве исходной
можно взять любую точку одномерного
пространства. Тогда в узлах ряда окажутся
точки, во всех отношениях эквивалентные
исходной. Перемещение фигур при этом
может происходить в прямом и обратном
направлениях.
Узловые ряды образуют двухмерные узловые сетки, с помощью которых можно описать расположение каких-либо частиц в бесконечном двухмерном узоре (например, в рисунке обоев) (рис.3) или, в частности, расположение атомов, ионов, молекул в атомных плоскостях кристаллической структуры.

Рис. 5.3. Двухмерный бесконечный узор и его «решетка» — узловая параллелограмматическая сетка. Тип плоской сетки не зависит от того, какая точка принята за исходную.
Периодичность
плоского узора выражается
параллелограмматической узловой сеткой
— двухмерной
решеткой. И
любой рисунок обоев или тканей может
быть совмещен с самим собой переносом
вдоль трансляционных векторов
и
![]() ,
лежащих в плоскости рисунка (рис. 5.4.).
Минимальным представителем двухмерной
решетки является параллелограмм,
построенный на двух неколлинеарных
векторах
и
,
лежащих в плоскости рисунка (рис. 5.4.).
Минимальным представителем двухмерной
решетки является параллелограмм,
построенный на двух неколлинеарных
векторах
и
![]() ,
называемый ячейкой
двухмерной решетки.
Очевидно, что подобные ячейки заполняют
все двухмерное пространство без
промежутков. В трехмерном регулярном
узоре, например в кристаллической
структуре, самосовмещение наступает
при переносе вдоль любого трансляционного
вектора. Периодичность такого узора
описывается трехмерной решеткой —
параллелепипедальной
узловой сеткой,
называемой пространственной
решеткой (рис.
5.5). Минимальным представителем трехмерной
решетки будет параллелепипед, ребрами
которого служат три некомпланарных
вектора
,
и
,
называемый ячейкой
двухмерной решетки.
Очевидно, что подобные ячейки заполняют
все двухмерное пространство без
промежутков. В трехмерном регулярном
узоре, например в кристаллической
структуре, самосовмещение наступает
при переносе вдоль любого трансляционного
вектора. Периодичность такого узора
описывается трехмерной решеткой —
параллелепипедальной
узловой сеткой,
называемой пространственной
решеткой (рис.
5.5). Минимальным представителем трехмерной
решетки будет параллелепипед, ребрами
которого служат три некомпланарных
вектора
,
и
![]() —
периоды идентичности вдоль трех узловых
рядов решетки.
—
периоды идентичности вдоль трех узловых
рядов решетки.
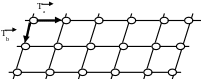
Рис. 5.4. Узловая сетка
Такой параллелепипед повторяемости, или идентичности, называют также ячейкой трехмерной решетки, которая также без остатка заполняет все трехмерное пространство.
Действительно, если в трехмерном пространстве выбрать какую-либо точку (не обязательно материальную) и посчитать ее одним из узлов решетки, то в остальных ее узлах окажутся все точки этого пространства, идентичные (физически и геометрически) исходной. Прикладывая решетку к другой заинтересовавшей нас точке при сохранении параллельности решетки самой себе, в ее узлах вновь получим все эквивалентные точки. В результате убеждаемся, что решетка не есть нечто материальное – не конкретная структура кристалла. Т.е. не конкретная укладка атомов (или фигур) в неподвижных узлах решетчатого каркаса, а математический образ — схема, с помощью которой мы описываем периодичность кристаллического вещества, не зависящая от того, какая точка трехмерного пространства (узора) принята за исходный узел. Иными словами, решетку удобно считать своеобразным элементом симметрии, размножающим точки пространства совершенно аналогично тому, как их размножают другие элементы симметрии — плоскости, оси и т.д. В этом смысле решетка — это свойство кристаллического состояния вещества, ибо любое кристаллическое вещество, даже лишенное каких-либо иных элементов симметрии, всегда обладает этим основным элементом симметрии — решеткой, или решетчатым строением.

Рис. 5.5. Пространственная решетка и ее ячейка
