Получение неравенства для ошибки, согласованная норма матрицы, подробнее про norm и cond
В этом разделе рассказывается:
почему в оценках, приведенных в разделе Влияние обусловленности матрицы на точность решения системы с ней, нельзя использовать любые матричные и векторные нормы (вычисляемые функцией norm) и как они должны быть связаны между собой;
как получается неравенство для ошибки в решении при возмущении правой части;
почему число обусловленности матрицы не может быть меньше единицы;
откуда берутся системы, для которых в оценке выполняется точное равенство (наихудший случай).
Итак, мы рассматриваем две системы: исходную (с точным решением x)
Ax = b
и вторую систему (с точным решением
),
в правую часть которой внесены возмущения
Продемонстрируем
вывод оценки
Из того, что Ax = b следует, что || Ax ||V = || b ||V (здесь введено обозначение || ||V для векторной нормы, и пока не так важно, какая именно выбрана). Далее требуется совершить такой переход
|| Ax ||V = || b ||V ⇒ || A ||M || x ||V ≥ || b ||V
где || ||M — некоторая матричная норма. Для того, чтобы это можно было сделать, матричная норма || ||M и векторная норма || ||V должны удовлетворять следующему неравенству
|| A ||M || x ||V ≥ || Ax ||V
для любых матриц A и векторов x. Если это неравенство выполняется, то матричная норма || ||M называется согласованной с векторной нормой || ||V. Известно, например, что спектральная норма
(квадратный корень из максимального собственного числа матрицы AT) согласована с евклидовой векторной нормой
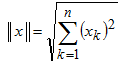
Именно поэтому в разделе Влияние обусловленности матрицы на точность решения системы с ней мы проводили все эксперименты с привлечением данных норм.
Получив неравенство || A ||M || x ||V ≥ || b ||V далее заметим, что из Ax = b и
следует, что
.
Поскольку матрица A невырожденная, то
отсюда следует, что δx = A-1δb и || δx ||V = ||
A-1δb ||V. Опять используем согласованность
норм и получаем неравенство || δx ||V ≤ ||
A-1 || M || δb || V. Далее в двух полученных
неравенствах
|| A ||M|| x ||V ≥ || b ||V и || δx ||V ≤ || A-1 || M || δb ||V
меньшую величину одного из неравенств делим на большую величину другого неравенства, а большую, соответственно, на меньшую
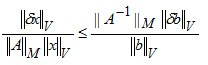
и простым преобразованием окончательно получаем требуемое неравенство
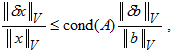
где cond(A) = || A ||M * || A-1 ||M.
Заметим, что при выводе неравенства для ошибки мы пользовались только тем, что матричная норма согласована с векторной. Данное верно не только для спектральной нормы матрицы и евклидовой нормы вектора, но и для других норм. Так, например максимальная столбцевая матричная норма, вычисляемая по формуле
согласована с первой векторной нормой
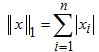
а максимальная строчная матричная норма, вычисляемая по формуле
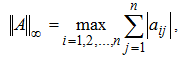
согласована с бесконечной векторной нормой
Функция norm вычисляет не только евклидову норму вектора и спектральную норму матрицы, но и перечисленные выше векторные и матричные нормы. Для этого ее требуется вызвать с дополнительным вторым аргументом:
q = norm(A, 1) — максимальная столбцевая норма матрицы A
q = norm(A, inf) — максимальная строчная норма матрицы A
q = norm(a, 1) — первая векторная норма a
q = norm(a, inf) — бесконечная векторная норма a
Число обусловленности матрицы cond(A) = || A ||M * || A-1 ||M относительно различных матричных норм может быть вычислено при помощи функции cond. Если cond вызывается с одним входным аргументом (матрицей), то вычисляется число обусловленности относительно спектральной матричной нормы. При вызове функции cond с дополнительным аргументом возвращаются числа обусловленности относительно указанной матричной нормы:
с = cond(A, 1) — число обусловленности относительно максимальной столбцевой нормы матрицы
с = cond(A, inf) — число обусловленности относительно максимальной строчной нормы матрицы
В качестве примера, демонстрирующего важность согласованности норы матрицы с нормой вектора в неравенстве для ошибки, приведем пример с матрицей A, вектором правой части b и вектором ошибок в правой части delta_b.
A = [2.1005632211074903e+009 2.4405728346208658e+009 2.6288320556007657e+009 3.9543845780862803e+009
5.6384551998346877e+008 6.5511289861702812e+008 7.0564654322518432e+008 1.0614591390422670e+009
1.9531852931707768e+009 2.2693394431935925e+009 2.4443901805698233e+009 3.6769404175323849e+009
2.2044117415857959e+009 2.5612308917984776e+009 2.7587973499916158e+009 4.1498830928366508e+009];
b = [ -5.7373057243726833e-001
-1.5400413072907607e-001
-5.3347697688693385e-001
-6.0209490373259589e-001];
delta_b = [-0.71685839091451e-5
0.54786619630709e-5
0.37746931527138e-5
0.20850322383081e-5];
Вычислим правую и левую часть оценки с использованием первой векторной нормы, а число обусловленности матрицы по отношению к спектральной матричной норме
RIGHT = norm(delta_b,1)/norm(b,1);
c = cond(A);
x = A\b;
x_tilda = A\(b+delta_b);
delta_x = x - x_tilda;
LEFT = norm(delta_x,1)/norm(x,1);
format short e
disp([LEFT c*RIGHT])
Получаем для левой и правой частей неравенства следующие значения
9.9484e+004 9.9323e+004
Левая часть не должна превосходить правую (по доказанному выше), однако получилась больше из-за выбора несогласованных норм.
Разберем теперь, почему число обусловленности матрицы не может быть меньше единицы. Число обусловленности матрицы A определяется как cond(A) = || A ||M * || A-1 ||M, где || A ||M — какая-то матричная норма A. Матричная норма (т.е. правило, по которому каждой матрице сопоставляется число) не может быть произвольной, она должна удовлетворять следующим четырем аксиомам:
A1. || A || ≥ 0 для любой матрицы A и || A || = 0 тогда и только тогда, когда A — нулевая матрица.
А2. || αA || = | α | * || A || для любой матрицы A и числа α.
А3. || A + B || ≤ || A || + || B || для любых матриц A и B
А4. || AB || ≤ || A || * || B || для любых матриц A и B.
Из последней аксиомы видно, что норма определена только для квадратных матриц (хотя, в приведенных выше формулах для вычисления различных норм, в принципе, нет такого ограничения). Кроме того, из последней аксиомы следует, что любая норма единичной матрицы I не меньше единицы, действительно
|| I || = || I*I || ≤ || I ||2 ⇒ || I || ≥ 1.
Тогда, опять с привлечением четвертой аксиомы, получаем, что число обусловленности матрицы всегда больше единицы (верно для числа обусловленности матрицы по отношению к произвольной матричной норме)
1 ≤ || I || = || AA-1 || ≤ || A || * || A-1 || = cond(A).
Завершим данный раздел исследованием причины появления точного равенства в оценке ошибки в решении при возмущении правой части:
и построением соответствующих примеров в MATLAB. (Приводимое ниже рассуждение содержится, например, в книге Дж. Форсайт, К Молер. Численное решение систем линейных алгебраических уравнений. М: «Мир», 1969.)
Существенную роль в рассуждениях играет теорема о сингулярном разложении матрицы, согласно которой для любой вещественной матрицы размера на существуют две ортогональные матрицы U и V размера n на n (UTU=UUT и VTV = VVT ) такие, что произведение D = UTAV является диагональной матрицей, причем можно выбрать U и V так, что
где μ1 ≥ μ2 ≥…≥μr ≥ μr+1 =…=μn=0, ,
а r — ранг матрицы A. Числа μk называют спектральными числами матрицы A. Для невырожденной матрицы A верно:
μ1 ≥ μ2 ≥ … ≥μn ≥ 0.
Следующий важный факт заключается в том, что умножение на ортогональную матрицу не изменяет евклидовой нормы вектора, т.е. для любого вектора x с n элементами и любой ортогональной матрицы U размера n на n верно равенство
|| Ux || = || x ||.
Поскольку умножение на ортогональную матрицу не изменяет спектральной нормы, то
следовательно для числа обусловленности матрицы верно равенство
У нас есть две системы: Ax = b (с точным решением x) и (с точным решением ). Очевидно, что ошибка δx является решением системы, правая часть которой является возмущением δb, т.е. системы Aδx = δb. Пусть D = UTAV есть сингулярное разложение матрицы A, тогда UDVT = A из-за того, что U и V — ортогональные матрицы. Далее
Ax = b ⇒ UDVTx = b.
Введем обозначения
x' = VTx, b' = UTb,
тогда следующие системы эквивалентны
Ax = b ⇔ Dx' = b'
Совершенно аналогично рассмотрим систему относительно ошибки
Aδx = δb ⇒ UDVTδx = δb
Вводим обозначения
δx' = VTδx, δb' = UTδb,
при которых следующие системы оказываются эквивалентны
Aδx = δb ⇔ Dδx' = δb'
Т.е. мы получили простые эквивалентные системы с диагональной матрицей, на диагонали которой стоят спектральные числа матрицы A.
Выберем теперь специальным образом правые части этих систем, именно, пусть
где β > 0, тогда соответствующее ей решение системы Dx' = b' будет
где μ1 — максимальное сингулярное число матрицы A. Схожим образом поступим и с системой Dδx' = δ b' , именно, пусть
Из сохранения нормы вектора при его перемножении с ортогональной матрицей следует, что
β/μ1 = || x' || = || VTx || = || x || и γ/μn = || δx' || = || VTδx || = ||δx ||.
Совершенно аналогично получаем равенства:
β = || b' || = || UTb || = || b || и γ = || δb' || = || UTδb || = || δb ||.
Тогда
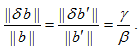
И
а поскольку
то окончательно получаем
Итак, для каждой матрицы A можно построить вектор правой части системы и его возмущение такие, что ошибка в решении будет произведением числа обусловленности матрицы на ошибку в правой части. В MATLAB соответствующее построение может быть выполнено и без использования сингулярного разложения (хотя оно может быть найдено при помощи функции svd).
Сначала задаем n и получаем две ортогональные матрицы U и V, выполняя QR-разложение матриц n на n из случайных чисел:
n = 4;
[U, R] = qr(rand(n));
[V, R] = qr(rand(n));
Далее создаем диагональную матрицу D заданными числами на диагонали, возьмем, к примеру, первый элемент 1010, а остальные единицы.
D = diag([1e10 ones(1,n-1)]);
После этого конструируем матрицу A, используя диагональную матрицу D и ортогональные матрицы U и V
A = U*D*V';
Число обусловленности матрицы A будет совпадать с числом обусловленности матрицы D, которое в нашем примере равно 1010
c = cond(A)
c =
1.0000e+010
Дальше задаем β > 0 и γ > 0, которые фигурировали в приведенных выше рассуждениях:
beta = 1;
gamma = 1e-5;
и строим вектора b' и δb'
b1 = [beta zeros(1,n-1)]';
db1 = [zeros(1,n-1) gamma]';
по которым находим вектора b и δb
b = U*b1;
db = U*db1;
Далее решаем системы Ax = b и
x = A\b;
x_tilda = A\(b+db);
вычисляем левую и правую части неравенства
dx = x - x_tilda;
RIGHT = norm(db)/norm(b);
LEFT = norm(dx)/norm(x);
и выводим их
format short e
disp([LEFT c*RIGHT])
Получаем равенство
1.0000e+005 = 1.0000e+005