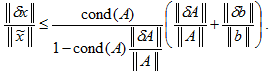Влияние обусловленности матрицы на точность решения системы с ней
В этом разделе мы рассмотрим, как ошибки в элементах вектора правой части и в матрице системы линейных уравнений Ax = b могут повлиять на решение этой системы. Обратимся сначала к случаю внесения возмущений в вектор правой части b. Итак, мы решаем две системы
причем предполагается, что каждую из систем мы решаем точно, а основной возникающий вопрос — насколько будет отличаться решение x системы (1) от решения системы (2) с возмущением в правой части δb. Это довольно важный вопрос, поскольку элементы правой части могут быть получены как результат некоторых измерений, соответственно содержащий погрешность δbk в каждой компоненте bk. Хотелось бы, чтобы при измерении одной и той же величины (каждый раз со своими, небольшими погрешностями) соответствующие решения систем с мало отличающимися правыми частями также не очень сильно отличались друг от друга. К сожалению, так бывает не всегда. Причиной этому — характеристика матрицы, называемая ее обусловленностью. Об этом и пойдет дальше речь.
Сначала требуется ввести меру близости
векторов
и
x, т.е. вектора ошибки
. Мерой величины вектора является норма
(определяться она может по-разному).
Возьмем пока в качестве нормы обычную
евклидову норму вектора (квадратный
корень из суммы квадратов его компонент),
т.е.
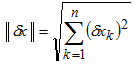соответственно
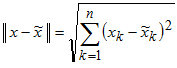
где n — число неизвестных и уравнений в системе. Кроме векторной нормы для оценки величины вектора нам понадобится еще и матричная норма для оценки величины матрицы. Возьмем матричную норму, которая определяется следующим образом (она называется спектральной):
т.е. спектральная матричная норма равна квадратному корню из максимального собственного числа матрицы ATA. В MATLAB имеется функция norm для вычисления норм матриц и векторов, которая, в частности, умеет вычислять приведенные выше нормы. Почему мы выбрали именно такие нормы векторов и матриц, подробно объясняется в разделе Получение неравенства для ошибки, согласованная норма матрицы, где приведено немного выкладок и определений. Это связано с оценкой, которой мы будем пользоваться для ошибки в решении системы (вывод этого неравенства также приведен в упомянутом разделе):
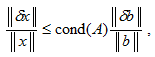
Здесь через обозначено число обусловленности матрицы , которое определяется так:
Из приведенного неравенства следует,
что чем больше число обусловленности
матрицы системы, тем больше может быть
относительная ошибка в решении
при небольшой ошибке в правой части
Рассмотрим классический пример плохо обусловленной матрицы — матрицу Гильберта — и выясним, как ошибка в правой части системы влияет на ошибку в решении. Матрица Гильберта определяется следующим образом
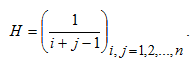
Для создания матрицы Гильберта в MATLAB предусмотрена функция hilb, входной аргумент которой задает размер матрицы. Возьмем небольшую матрицу 6 на 6:
n = 6;
H = hilb(n)
H =
1.0000 0.5000 0.3333 0.2500 0.2000 0.1667
0.5000 0.3333 0.2500 0.2000 0.1667 0.1429
0.3333 0.2500 0.2000 0.1667 0.1429 0.1250
0.2500 0.2000 0.1667 0.1429 0.1250 0.1111
0.2000 0.1667 0.1429 0.1250 0.1111 0.1000
0.1667 0.1429 0.1250 0.1111 0.1000 0.0909
Далее вычислим такую правую часть системы b, что все компоненты ее решения x равны единице:
x = ones(n, 1);
b = H*x
b =
2.4500
1.5929
1.2179
0.9956
0.8456
0.7365
Видим, что ни в матрице, ни в векторе правой части нет ничего «подозрительного», все числа не сильно отличаются друг от друга. Теперь сформируем возмущенную правую часть b + δb, добавив в вектор b небольшие числа порядка 10-5 и решим систему с возмущенной правой частью для получения вектора .
delta_b = 1e-5*(1:n)';
x_tilda = H\(b + delta_b)
x_tilda =
0.9978
1.0735
0.4288
2.6632
-1.0160
1.8593
Видно, что полученное решение далеко от точного, где должны быть все единицы. Вычислим относительную ошибку в решении и в правой части (функция norm по умолчанию вычисляет евклидову норму вектора):
delta_x = x - x_tilda;
LEFT = norm(delta_x)/norm(x)
LEFT =
1.1475
RIGHT = norm(delta_b)/norm(b)
RIGHT =
2.7231e-005
Итак, ошибка в решении порядка единицы, хотя изменения в правой части были порядка 10-5. Это полностью укладывается в приведенное выше неравенство для ошибки. Действительно, вычислим число обусловленности cond(H) при помощи функции MATLAB, которая называется cond и по умолчанию вычисляет
для спектральной нормы матрицы
c = cond(H)
c =
1.4951e+007
Итак
= LEFT ≈ 1.1475 меньше
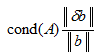= c* RIGHT ? 1.4951e+07 * 2.7231e-05 ≈ 407
и неравенство выполнено (даже с некоторым запасом).
При увеличении размера матрицы Гильберта ошибка в решении будет только расти (это несложно проверить, задавая n = 7, 8, …). Причем, при n = 12 выведется сообщение о том, что матрица плохообусловлена и решение может оказаться неверным
Warning: Matrix is close to singular or badly scaled.
Results may be inaccurate. RCOND = 2.409320e-017.
В качестве меры обусловленности здесь выбрана величина RCOND равная единице, деленной на оценку числа обусловленности (число обусловленности оценивается по достаточно быстрому алгоритму, который работает намного быстрее, чем cond, о чем более подробно написано в справке по функции rcond). Если значение RCOND мало, то матрица считается плохообусловленной.
Увеличение ошибки в решении при увеличении размера матрицы Гильберта происходит из-за того, что число обусловленности матрицы Гильберта растет очень быстро с ее размером. В этом несложно убедиться при помощи простого цикла и функции semilogy (масштаб по оси ординат — логарифмический):
N = 1:20; C = zeros(1, 20);
for n = N
H = hilb(n);
C(n) = cond(H);
end
semilogy(N, C)
grid on, title('cond(H)'), xlabel('n')
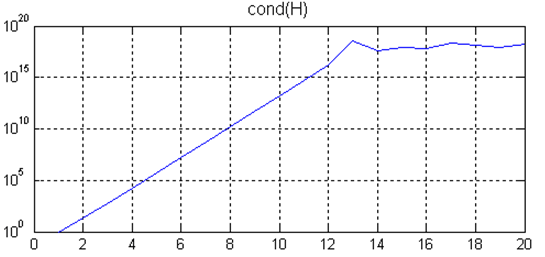
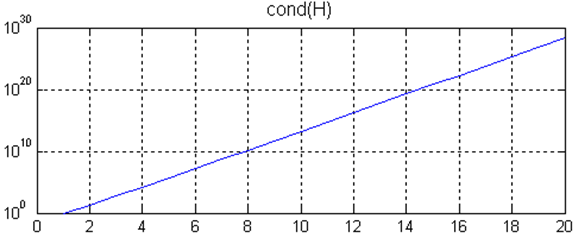
Кстати, поскольку функция cond находит число обусловленности при помощи численного метода (а именно сингулярного разложения для нахождения сингулярных чисел), то число обусловленности после n = 12 вычисляется уже неверно, на самом деле оно должно расти и дальше, в чем можно убедиться при помощи символьных вычислений в MATLAB и операций с заданным числом значащих цифр
N = 1:20; C = zeros(1, N);
digits(60)
for n = N
H = vpa(sym(hilb(n))); % вычисление матрицы Гильберта с точностью до 60-го знака
sigma = svd(H); % нахождение сингулярных чисел матрицы Гильберта
% вычисление числа обусловленности матрицы Гильберта
C(n) = max(double(sigma))/min(double(sigma));
end
semilogy(N, C)
grid on, title('cond(H)'), xlabel('n')
Рассмотрим теперь три важных момента, касающихся данного примера.
Первый из них — решение системы Hx = b (с вектором правой части, соответствующим решению из единиц) при помощи оператора обратной косой черты не даст точные единицы, погрешность будет уже в десятом знаке (хотя в MATLAB все вычисления по умолчанию выполняются с двойной точностью)
format long
H\b
ans =
0.99999999999916
1.00000000002391
0.99999999983793
1.00000000042209
0.99999999953366
1.00000000018389
Так происходит из-за того, что при вычислении вектора b при умножении матрицы H на вектор из всех единиц мы уже заложили в него некоторую погрешность. Кроме того, ошибки округления в процессе решения системы также сыграли свою роль и плохая обусловленность матрицы (даже небольшого размера) привела к таким ошибкам в решении. Действительно, для матриц небольшого размера с небольшим числом обусловленности такого эффекта наблюдаться не будет. Возьмем матрицу 6 на 6 из случайных чисел, вычислим ее число обусловленности
A = rand(n);
cond(A)
ans =
57.35245279907571
Затем сформируем правую часть, соответствующую точному решению из всех единиц
x = ones(n, 1);
b = A*x;
и решим систему, получив в результате хорошую точность
>> A\b
ans =
1.00000000000000
1.00000000000000
1.00000000000000
1.00000000000000
1.00000000000000
1.00000000000000
Второй важный момент связан с определителем матрицы. Вычислим определитель матрицы Гильберта размера 6 на 6, с которой мы решали систему
>> det(hilb(6))
ans =
5.3673e-018
Определитель оказывается достаточно мал, откуда можно сделать неверный вывод, что источник проблемы большой ошибки в решении при небольшом возмущении правой части системы — малость определителя. В действительности это не так, если определитель системы мал, то это не означает плохой обусловленности матрицы и, следовательно, большой ошибки в решении. Действительно, возьмем матрицу
A = [1e-40 1e-42 1e-42
1e-42 1e-40 1e-42
1e-42 1e-42 1e-40];
Ее определитель очень мал, порядка 10-121
det(A)
ans =
9.9970e-121
(слово «очень», конечно условно, но он меньше определителя матрицы Гильберта размера 6 на 6, при решении системы с которой у нас возникли проблемы). Однако, малость определителя никак не повлияет на ошибку в решении при возмущении правой части системы, что несложно показать, сформировав систему с известным решением, внеся возмущения в правую часть и решив систему:
x = [1e40; 1e40; 1e40];
b = A*x;
delta_b = 1e-5*[1; 2; 3];
x_tilda = A\(b+delta_b);
delta_x = x - x_tilda;
LEFT = norm(delta_x)/norm(x)
RIGHT = norm(delta_b)/norm(b)
LEFT =
2.1272e-005
RIGHT =
2.1179e-005
Итак, относительная ошибка в решении практически равна относительной ошибке в правой части, поскольку число обусловленности приведенной выше матрицы A немного больше 1, а именно:
c = cond(A)
c =
1.0303
И, наконец, рассмотрим третий вопрос, касающийся достижения знака равенства в неравенстве для ошибки в решении
Т.е., говоря другими словами, выясним: может ли быть такая ситуация, когда мы делаем небольшое относительное возмущение правой части системы, скажем 10-5, число обусловленности матрицы системы равно 1010, а в решении получается относительная ошибка 105. Можно проделать массу примеров, перебирая различные матрицы, не получить достижения равенства и ошибочно заключить, что это всего лишь завышенная оценка сверху для ошибки в решении. Однако, это не так, в чем нас убеждает следующий пример
A = [2.1005632211074903e+009 2.4405728346208658e+009 2.6288320556007657e+009 3.9543845780862803e+009
5.6384551998346877e+008 6.5511289861702812e+008 7.0564654322518432e+008 1.0614591390422670e+009
1.9531852931707768e+009 2.2693394431935925e+009 2.4443901805698233e+009 3.6769404175323849e+009
2.2044117415857959e+009 2.5612308917984776e+009 2.7587973499916158e+009 4.1498830928366508e+009];
b = [ -5.7373057243726833e-001
-1.5400413072907607e-001
-5.3347697688693385e-001
-6.0209490373259589e-001];
delta_b = [-0.71685839091451e-5
0.54786619630709e-5
0.37746931527138e-5
0.20850322383081e-5];
в котором относительное возмущение правой части равно 10-5
RIGHT = norm(delta_b)/norm(b)
RIGHT =
1.0000e-005
Относительная ошибка в решении системы оказывается 105
x = A\b;
x_tilda = A\(b+delta_b);
delta_x = x - x_tilda;
LEFT = norm(delta_x)/norm(x)
LEFT =
1.0000e+005
И происходит так потому, что
1) в этом примере число обусловленности матрицы A равно 1010;
c = cond(A)
c =
1.0000e+010
2) неравенство для ошибки в решении переходит в равенство.
Если установить формат long, то мы увидим, что LEFT, RIGHT и число обусловленности не в точности 105, 10-5 и 1010, соответственно, но это вызвано ошибками округлений. При решении в точной арифметике, равенство получилось бы точным, что можно показать аналитически (см. раздел Получение неравенства для ошибки, согласованная норма матрицы, подробнее про norm и cond).
В предыдущих примерах мы предполагали, что матрица не содержит ошибок, а ошибки могут быть только в правой части системы линейных уравнений. На практике может оказаться, что элементы матрицы системы заданы с ошибками, т.е. вместо системы
Ax = b
мы решаем систему
В этом случае мы так же можем оценить погрешность в решении, и в оценку снова входит число обусловленности матрицы
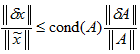
В самом общем случае ошибки могут быть как в матрице, так и в векторе правой части, и соответствующая оценка погрешности в решении имеет более сложный вид
