Алгоритм решения системы линейных уравнений при помощи знака обратной косой черты
При решении в MATLAB системы линейных алгебраических уравнений при помощи знака обратной косой черты x = A\b
работает алгоритм, который в зависимости от типа матрицы решает систему при помощи наиболее подходящего метода, реализованного в одной из процедур пакета LAPACK или UMFPACK. Здесь b может быть и матрицей, число строк которой совпадает с числом строк матрицы A. Тогда возвращается матрица x, каждый i-ый ее столбец содержит решение системы Ax(i) = b(i), i=1,2,...,k, где b(i) — i-ый столбец матрицы b = [ b(1) | b(2)...| b(k) ].
Алгоритм, реализованный в операции \ состоит из следующих шагов:
1. В тривиальном случае, если A разреженная и диагональная (разреженным матрицам в MATLAB посвящен раздел Разреженные матрицы), решение находится по простой формуле xk = bk/akk, где k=1,2,...n.
2. Если A — квадратная, разреженная и ленточная матрица, то используется солвер для ленточных матриц. При этом могут быть два варианта:
a. Если A — трехдиагональная матрица и b — один столбец из вещественных чисел, тогда система решается гауссовым исключением (его операции совершаются только с элементами на диагоналях). Если в процессе исключения для сохранения устойчивости потребуется сделать перестановки строк, или если матрица A не является трехдиагональной, то работает следующий пункт.
b. Если A — ленточная с плотностью ненулевых элементов больше параметра bandden, по умолчанию равного 0.5, или не выполняются условия предыдущего пункта, тогда, в зависимости от типа A и b (double или single) вызываются следующие процедуры библиотеки LAPACK:
A и b вещественные типа double — процедуры DGBTRF, DGBTRS
A и b комплексные типа double — процедуры ZGBTRF, ZGBTRS
A или b вещественные типа single — процедуры SGBTRF, SGBTRS
A или b комплексные типа single — процедуры CGBTRF, CGBTRS
Под плотностью ненулевых элементов понимают отношение числа ненулевых элементов в ленте к числу всех элементов в ленте матрицы, например для матрицы 7 на 7, шаблон которой приведен ниже, число ненулевых элементов
nz = 1 (на диаг.№-2) + 6 (на диаг.№-1) + 7 (на диаг.№0) + 6 (на диаг.№1) + 1 (на диаг.№2) + 1 (на диаг.№3) = 22, а число всех элементов в ленте
band = 5 (на диаг.№-2) + 6 (на диаг.№-1) + 7 (на диаг.№0) + 6 (на диаг.№1) + 5 (на диаг.№2) + 4 (на диаг.№3) = 33 и плотность ненулевых элементов будет 2/3. Поскольку 2/3 > 0.5, то будет применен солвер для ленточных матриц
Параметр bandden, как и другие параметры, управляющие алгоритмами для разреженных матриц в MATLAB, устанавливается при помощи функции spparms.
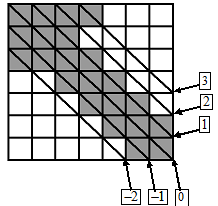
Смысл данного шага алгоритма в том, что решение системы с ленточной матрицей не требует действий вне ленты. Если лента достаточно сильно заполнена, то действий с нулевыми элементами будет не очень много. Напротив, если лента достаточно сильно разрежена, то больший эффект могут принести подходы, приведенные в дальнейших шагах алгоритма.
3. Если A — верхняя или нижняя треугольная матрица, то применяется метод обратной подстановки, или, соответственно, метод прямой подстановки, в котором из последнего (или первого уравнения) находится компонента решения и далее найденные компоненты подставляются в следующие уравнения для нахождения очередных компонент решения системы уравнений.
4. Если A — может быть приведена перестановками к треугольной форме, то выполняется соответствующее приведение, а далее система уравнений решается как и в п.3.
5. Если A — симметричная матрица (или, в комплексном случае, эрмитова), на ее диагонали находятся только положительные вещественные элементы, то в зависимости от того, разрежена A или нет, выполняется п. а) или п. б).
a. Если А не является разреженной, тогда делается попытка выполнить разложение Холецкого A = RT R с последующим решением систем с треугольными матрицами RT и R: RTy = b и Rx = y. При этом вызываются следующие процедуры библиотеки LAPACK:
A и b вещественные и типа double — DLANGE, DPOTRF, DPOTRS, DPOCON
A и b комплексные и типа double — ZLANGE, ZPOTRF, ZPOTRS, ZPOCON
A и b вещественные и типа single — SLANGE, SPOTRF, SPOTRS, SDPOCON
A и b комплексные и типа single — CLANGE, CPOTRF, CPOTRS, CPOCON
Разложение Холецкого закончится неудачно, если матрица не является положительно определенной. Но предварительной проверки на положительную определенность не производится, а она определяется именно в процессе разложения, поскольку довольно часто достаточно выполнить несколько шагов разложения Холецкого для выяснения того факта, что матрица не положительно определенная (в процессе вычислений возникает необходимость извлечь квадратный корень из отрицательного числа). Если разложение Холецкого не выполнилось, то переходим к следующему пункту.
b. Если А разрежена, то предварительно выполняются симметричные перестановки строк и столбцов по симметричному алгоритму минимальной степени (функцией symmmd) для уменьшения заполнения множителя разложения Холецкого, т.е. для уменьшения числа новых ненулевых элементов, возникающих в процессе заполнения:
p = symmmd(A) — в вектор p записаны перестановки
Далее производится разложение Холецкого матрицы со сделанными перестановками
R = chol(A(p, p));
и решаются две системы с множителями Холецкого, первая с транспонированным множителем и соответствующими перестановками в векторе правой части
y = R' \ b(p);
и вторая, с множителем разложения и с занесением компонент решения на соответствующие позиции в векторе x
x(p, :) = R \ y
6. Если A — хессенбергова матрица, то она приводится к верхней треугольной (с соответствующей модификацией правой части) и затем система решается подстановками
7. Если A — квадратная матрица, не удовлетворяющая условиям пунктов 1-6, то в зависимости от того, разрежена она или нет, выполняются следующие действия
a. Если A не является разреженной матрицей, то при помощи исключения Гаусса с выбором ведущего элемента (для обеспечения устойчивости разложения) выполняется LU-разложение матрицы A = LU, где
U — верхняя треугольная матрица
L — матрица, перестановками строк сводящаяся к треугольной
и решение системы Ax = b находится последовательным решением систем с треугольными матрицами Ly = b, Ux = y.
Для выполнения LU-разложения вызываются следующие процедуры библиотеки LAPACK:
A и b вещественные и типа double — DLANGE, DGESV, DGECON
A и b комплексные и типа double — ZLANGE, ZGESV, ZGECON
A и b вещественные и типа single — SLANGE, SGESV, SGECON
A и b комплексные и типа single — CLANGE, CGESV, CGECON
b. Если A — разреженная матрица, то производится перестановка столбцов с целью уменьшения заполнения множителей L и U в процессе нахождения разложения. Далее перестановкой строк в процессе LU-разложения обеспечивается вычислительная устойчивость, после которого снова решаются системы с треугольными матрицами. Для выполнения LU-разложения разреженной матрицы используются процедуры библиотеки UMFPACK
8. Если предыдущие пункты алгоритма не сработали и, следовательно, A не является квадратной матрицей, то все определяется ее разреженностью и работает один из приведенных ниже пунктов:
a. Если A не является разреженной матрицей, то выполняется QR-разложение AP = QR, где P — матрица перестановки столбцов, Q — ортогональная матрица (QTQ = I), а R — верхняя треугольная. Если A размера m на n, то Q размера m на m, а R размера m на n. Далее решение системы находится так:
x = P*(R \ (Q' * b))
поскольку из Ax = b и AP = QR следует: QRx = bP и Rx = QTbP.
b. В случае разреженной и прямоугольной матрицы A нет смысла вычислять матрицу Q, поскольку она скорее всего окажется заполненной. Поэтому в ходе алгоритма QR-разложения вычисляется c = QTb (т.е. модифицированная правая часть) и решается система Rx = c с треугольной матрицей для получения решения исходной системы Ax = b.
Кроме всего перечисленного, в приведенном выше алгоритме оценивается обусловленность матрицы и выводится предупреждение о возможной погрешности в решении, если матрица плохообусловлена (см. раздел Влияние обусловленности матрицы на точность решения системы с ней). Приведенный алгоритм содержит всевозможные проверки, которые могут занять ощутимое дополнительное время. В следующем разделе Функция linsolve для решения систем линейных уравнений приводится функция linsolve, которая позволяет задать тип матрицы, таким образом сократив время вычислений.