Матричные разложения Холецкого, lu и qr

В MATLAB есть функции для следующих разложений:

разложения Холецкого — функция chol;

LU-разложения — функция lu;

QR-разложения — функция qr.

Разложения помогают эффективно решить целый набор систем линейных алгебраических уравнений с одной и той же матрицей и несколькими векторами правой части. Рассмотрим такой набор систем:

Ax=f(k), k=1, 2,...,N.

Предположим, что матрица A представлена в виде произведения двух матриц, причем системы с матрицами A=BC причем системы с матрицами B и C решаются значительно быстрее, чем с матрицей A. Тогда решения исходных систем получаются следующим образом. Поскольку Ax=f(k) и A=BC, то BCx=f(k) и решая последовательно By=f(k) и Cx=y находим решение k-ой системы. Для заполненных матриц разложение выполняется за O(n3) операций, где n — размер матрицы (т.е. за то же время, что и решение системы), а решение системы с каждым множителем разложения за O(n2) операций. Поэтому решение N систем c с предварительным разложением занимает O(n3)+O(n2)N. Решение же каждой системы без разложения матрицы потребовало бы O(n3)N арифметических действий.

Разложение Холецкого для заданной матрицы A заключается в нахождении такой верхней треугольной матрицы R с положительными диагональными элементами, что A=RTR. Известно, что если матрица A симметрична и положительно определена (т.е. для любого вектораx верно: xTAx0, или, что тоже самое, все собственные числа матрицы положительны), то разложение Холецкого существует и при том единственно.

Рассмотрим в качестве примера разложение Холецкого матрицы

A = [4 1 1

1 4 1

1 1 4];

R = chol(A)

R =

2.0000 0.5000 0.5000

0 1.9365 0.3873

0 0 1.8974

Простая проверка убеждает, что разложение выполнено верно (с точностью до возникающих погрешностей при операциях над вещественными числами)

A - R'*R

ans =

1.0e-015 *

0 0 0

0 0 0

0 0 0.4441

Если матрица не является положительно определенной, то это выяснится в процессе разложения, т.к. возникнет необходимость извлечения корня из отрицательного числа и выводится соответствующее предупреждение:

A = [1 4 4

4 1 4

4 4 1];

R = chol(A)

??? Error using ==> chol

Matrix must be positive definite.

Функция chol не проверяет матрицу на симметричность. При вычислениях используются элементы исходной матрицы, расположенные на диагонали и выше:

A = [4 1 2

1 4 1

1 1 4];

R = chol(A)

R =

2.0000 0.5000 1.0000

0 1.9365 0.2582

0 0 1.7127

A - R'*R

ans =

0 0 0

0 0 0

-1 0 0

Для произвольной квадратной матрицы можно выполнить LU-разложение, т.е. найти нижнюю треугольную матрицу L и верхнюю треугольную матрицу U такие, что A=LU. Более строгое утверждение формулируется следующим образом.

Если Ak — главный минор квадратной матрицы A размера n, составленный из первых k строк и столбцов (т.е. А(1:k, 1:k)) и det(Ak)0 для k=1,2,..., n-1, то существует единственная нижняя треугольная матрица L, диагональ которой состоит из единиц, и единственная верхняя треугольная матрица U такие, что A=LU.

При вычислении LULU-разложения может понадобится перестановка строк для обеспечения численной устойчивости процесса разложения, поэтому функция lu может вернуть матрицу L, которая является нижней треугольной с точностью до перестановки строк, например:

A = [0 1 1

2 3 1

1 2 5];

[L, U] = lu(A)

L =

0 1.0000 0

1.0000 0 0

0.5000 0.5000 1.0000

U =

2 3 1

0 1 1

0 0 4

Произведение LU где L — треугольная с точностью до перестановки строк, и будет равно матрице A (вообще говоря, с учетом погрешности при операциях с вещественными числами).

A-L*U

ans =

0 0 0

0 0 0

0 0 0

Если для матрицы A сделано разложение Холецкого или LU -разложение, то решение системы с матрицей A, как уже было сказано выше, сводится к решению двух систем с треугольными матрицами. Это решение может быть выполнено при помощи операции обратной косой черты, поскольку заложенный в ней алгоритм определяет треугольные матрицы и применяет эффективный способ решения системы с ними, требующий O(n2) арифметических действий. Рассмотрим пример решения системы

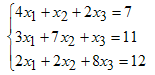
с предварительным LU-разложением матрицы.

A = [4 1 2

3 7 1

2 2 8];

f = [7; 11; 12];

Выполняем LU-разложение

[L, U] = lu(A);

и решаем последовательно две системы с треугольными матрицами, сначала с L, затем с U

y = L\f;

x = U\y

x =

1

1

1

Решение двух систем можно записать одним выражением

x = U\(L\f)

и результат получится тем же самым. Следует обратить внимание на важность использования скобок для определения порядка решения систем с треугольными матрицами. Выражение без скобок

x = U\L\f

приведет к совсем другому результату, поскольку сначала выполняется U\L, что эквивалентно (как было разобрано выше) решению систем с матрицей U и столбцами L в качестве векторов правой части. В результате получится матрица, каждый столбец которой является решением соответствующей системы, затем с этой матрицей и вектором правой части f решится система. Этот процесс, очевидно, не имеет ничего общего с решением исходной системы.

Рассмотрим последнее матричное разложение — QR-разложение, выполняемое функцией qr. QR-разложение может быть проделано для прямоугольных матриц, именно если A матрица размера m на n, то существует ортогональная матрица Q размера m на m (т.е. такая, что Q-1=QT) и матрица R размера m на n со всеми нулевыми элементами под главной диагональю, что A=QR .

QR-разложение отличается хорошей вычислительной устойчивостью и применяется, в частности, при приближении данных методом наименьших квадратов. В качестве примера рассмотрим решение предыдущей системы при помощи QR-разложения:

[Q, R] = qr(A)

Q =

-0.7428 0.6000 -0.2971

-0.5571 -0.8000 -0.2228

-0.3714 0.0000 0.9285

R =

-5.3852 -5.3852 -5.0138

0 -5.0000 0.4000

0 0 6.6108

После того, как сделано QR-разложение, решение системы Ax=f может быть найдено как решение системы с треугольной матрицей R, т.к. поскольку QR=f, то Rx=QTf:

>> x = R\(Q'*f)

x =

1.0000

1.0000

1.0000

Более подробно про матричные разложения, соответствующие функции MATLAB chol, lu и qr и их аргументы написано в разделе Матричные разложения.