ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ. МЕХАНИЧЕСКИЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА.

В классической механике справедлив механический принцип относительности, или принцип относительности Галилея: основы динамики одинаковы во всех инерциальных системах отсчета.

Для доказательства рассмотрим две системы отсчета – инерциальную систему K с координатами (x; y; z), которую будем условно считать неподвижной, и систему K с координатами (x; y; z), движущуюся относительно K равномерно и прямолинейно со скоростью u = const.

Отсчет времени начнем с момента, когда начала координат обеих систем совпадают.

Пусть в произвольный момент времени расположение систем имеет вид (см. рисунок). Скорость u направлена вдоль OO, тогда

Найдем связь между координатами произвольной точки A в обеих системах. Т.к.

запишем уравнение (1) в проекциях на оси координат.

x = x + u_xt, y = y + u_yt, z = z + u_zt (2)

Уравнения (1) и (2) называются преобразованиями Галилея. В частном случае система K движется со скоростью v вдоль положительного направления оси x системы K. Если в начальный момент времени оси координат совпадают, то преобразования Галилея имеют вид:

x = x + vt, y = y, z = z.

В классической механике предполагается, что ход времени не зависит от относительного движения системы отсчета, т.е. к преобразованиям (2) можно добавить

t = t (3)

Продифференцировав выражение (1) по времени с учетом выражения (3), получим:

v = v + u (4),

которое представляет собой правило сложения скоростей классической механики.

Ускорение точки A в системах отсчета K и K, движущихся друг относительно друга равномерно и прямолинейно, одинаково

a = a (5)

Следовательно, если на точку A другие тела не действуют, т.е. ускорение равно нулю, то согласно выражению (5) a = 0, т.е. система K является инерциальной. Таким образом, из соотношения (5) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяется, т.е. является инвариантным по отношению к преобразованиям координат.

Галилей обратил внимание, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно, т.е. не привязав себя к другой инерциальной системе отсчета.

Записанные соотношения справедливы в случае классической механики, т.е. u, v << c.

Для скоростей, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.

НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА.

Как мы уже говорили, законы Ньютона выполняются только в инерциальных системах отсчета.

ОПРЕДЕЛЕНИЕ: Системы отсчета, движущиеся относительно инерциальных систем отсчета с ускорением, называются неинерциальными.

В неинерциальных системах отсчета, строго говоря, законы Ньютона не выполняются, однако, законы динамики можно применять для них, если кроме сил, обусловленных воздействием тел друг на друга, ввести в рассмотрение силы особого рода, называемые силами инерции. Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил действующих на данное тело, включая и силы инерции. Силы инерции при этом должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение a, каким оно обладает в инерциальных системах отсчета.

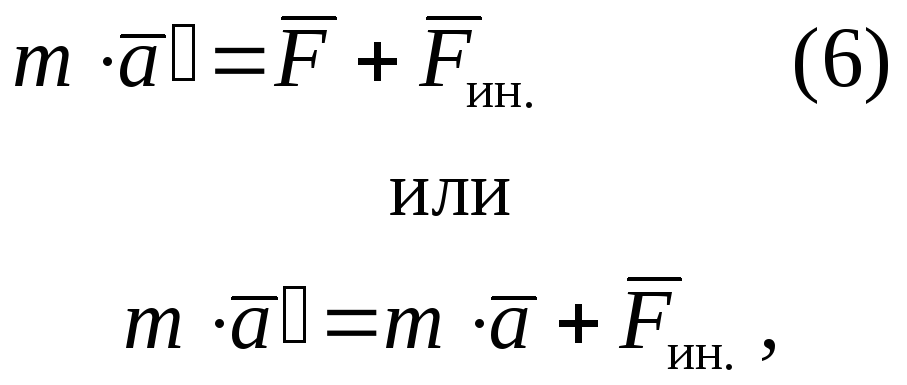
где a – ускорение тела инерциальной системы отсчета.

Рассмотрим следующие случаи:

I. Силы инерции при ускоренном поступательном движении системы отсчета.

П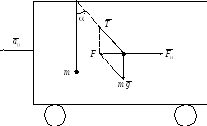усть на тележке к штативу подвешен шарик массой m. Пока тележка покоится или движется равномерно и прямолинейно, нить занимает вертикальное положение и сила тяжести уравновешена силой натяжения нити. Если тележке придать ускорение a₀, то нить начнет отклоняться от вертикального положения на угол  пока результирующая сила

не обеспечит ускорение шарика равное a₀. Таким образом,

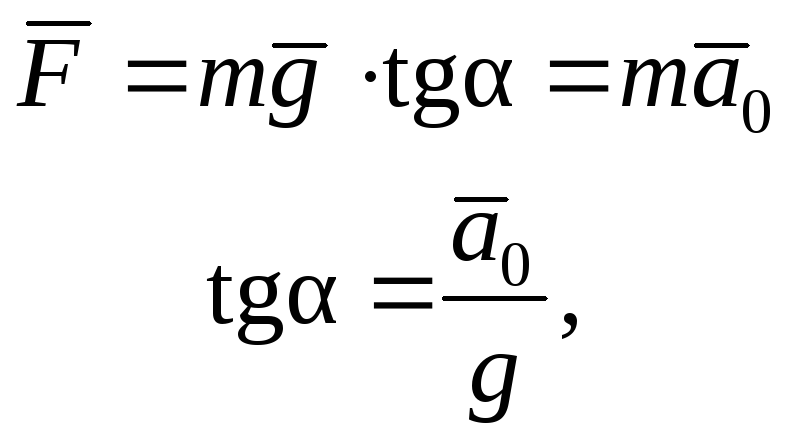
т.е. угол отклонения тем больше, чем больше ускорение тележки. Относительно системы отсчета, связанной с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешена силой инерции, т.е.

Примеры рассмотреть самостоятельно.

II. Силы инерции, действующие на тело, покоящееся во вращательной системе отсчета.

Пусть диск равномерно вращается с угловой скоростью  вокруг оси, проходящей через его центр. Пусть на диске на разных расстояниях друг от друга установлены маятники.

В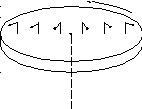 инерциальной системе отсчета, связанной с комнатой, где установлен диск, шарик равномерно вращается по окружности радиусом R относительно оси проходящей через центр диска. Следовательно, на него действует сила

F = m²R.

Она является равнодействующей силе тяжести и силе напряжения нити.

Когда движение шарика установится

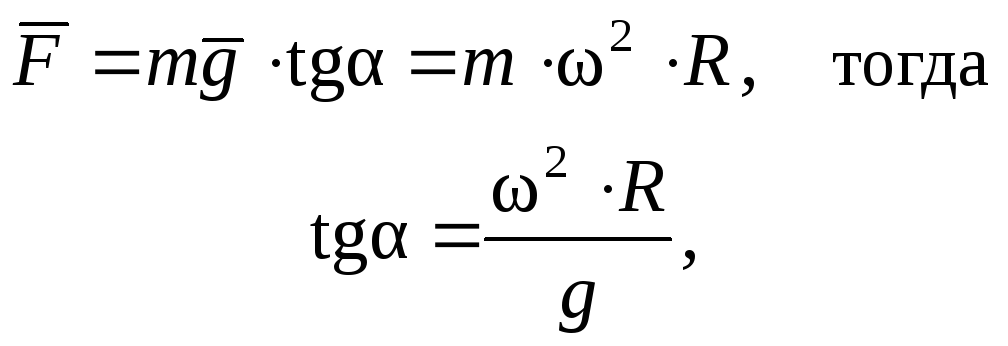
т.е. углы отклонения нитей маятников будут тем больше, чем больше радиус R и угловая скорость . Относительно системы отсчета, связанной с диском, шарик покоится, т.к. сила F уравновешивается противоположно направленной центробежной силой инерции, которая направлена от оси вращения диска и равна

F_ц = –m²R (8)

Примеры рассмотреть самостоятельно.

ОПРЕДЕЛЕНИЕ: Центробежная сила инерции, действующая на тела во вращающихся системах отсчета в направлении радиуса от оси вращения, зависит от угловой скорости вращения системы отсчета и радиуса R, но не зависит от скорости тел относительно вращающейся системы отсчета.

III. Силы инерции, действующие на тело, движущееся во вращательной системе отсчета.

П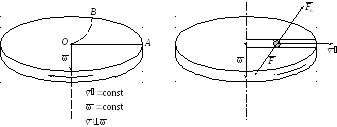усть шарик массой m движется с постоянной скоростью v вдоль радиуса равномерно вращающегося диска, при этом v.

Если диск не вращается, то шарик, направленный вдоль радиуса, попадает в точку A. Если диск привести во вращение в направлении указанном стрелкой, то шарик будет катиться по кривой OB. Его скорость v относительно диска меняет свое направление под действием некоторой силы, перпендикулярной скорости. Чтобы заставить шарик катиться по радиусу используем жестко укрепленный стержень, на котором шарик движется равномерно и прямолинейно со скоростью v. При отклонении шарика стержень действует на него с некоторой силой F. Относительно диска шарик движется равномерно и прямолинейно, что можно объяснить тем, что сила F уравновешивается силой F_к, силой инерции, перпендикулярной скорости, которая называется Кориолисовой силой.

Сила Кориолиса действует на тела, движущиеся относительно вращающейся системы отсчета.

Примеры рассмотреть самостоятельно.

Раскрываем в уравнении (6) силу инерции, получим основной закон динамики для неинерциальных систем отсчета:

Отметим, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Для любого из тел, находящегося в неинерциальной системе отсчета, силы инерции являются внешними, следовательно, в этом случае нет замкнутых систем. Это означает, что в неинерциальных системах отсчета не выполняются законы сохранения импульса, энергии и момента импульса. Таким образом, силы инерции действуют только в неинерциальных системах отсчета, в инерциальных системах таких сил не существует.