Вопрос9: Потенциальная энергия (вывод формулы).

Потенциальная энергия зависит от конфигурации системы и от взаимного расположения его частей и их положения во внешнем силовом поле.

А₁₂=П₁-П₂

она направлена в сторону уменьшения.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при бесконечно малом изменении конфигурации системы равна приращению потенциальной энергии (со знаком минус, т.к. работа совершается за счет убыли потенциальной энергии): dA = Fdr = -dП (здесь Fdr - скалярное произведение векторов). Из последнего соотношения по известной функции П(r) можно найти модуль и направление силы F.

Потенциальная энергия может быть определена исходя из последнего соотношения: П =-Fdr +С,

где С - постоянная интегрирования, т.е. потенциальная энергия определяется с точностью до произвольной величины. Однако это не отражается на физических законах, т.к. в них входит или разность потенциальных энергий в двух положениях тела или производная W_p по координатам. Поэтому в каждой конкретной задаче одну из конфигураций системы выбирают в качестве нулевой конфигурации, в которой потенциальную энергию системы полагают равной нулю (выбирают нулевой уровень отсчета и энергию системы в других положениях отсчитывают относительно нулевого уровня).

Таким образом, потенциальная энергия механической системы - это величина, равная работе, которую совершают все действующие на систему консервативные (потенциальные) силы при переводе системы из рассматриваемого состояния в состояние, соответствующее ее нулевой конфигурации . Конкретный вид функции П зависит от характера силового поля. Для консервативных сил F_x = -П/x, F_y = -П_p/y, F_z = -П/z

или в векторном виде F = -gradП = -[(П/x)i + (П/y)j + (П/z)k],

где i, j, k - орты координатных осей.

Вектор, определяемый выражением, называется градиентом скаляра П. Для него наряду с обозначением «gradП» применяется обозначение «П». Перевернутый треугольник называется оператором Набли, или оператором Гамильтона.

Конретный вид функции П зависит от характера силового поля. Потенциальная энергия тела массой m, поднятого на высоту h над поверхностью земли, рассчитывается как

П = mgh + с,

где c есть потенциальная энергия на нулевом уровне.

П=кх²/2 где К-коэффициент жесткости для пружин.

Вопрос10: Энергия. Закон сохран. Энергии. Графич. Представление энергии.

Закон сохранения энергии – это результат обобщения многих экспериментальных данных. Идея этого закона принадлежит Ломоносову, изложившему закон сохранения материи и движения, а полная формулировка в количественной форме дана немецким врачом Майером и ученым Гельмгольцем.

Рассмотрим систему материальных точек массами m₁, m₂, …, m_n, движущихся со скоростями v₁, v₂, …, v_n. Пусть F₁, F₂, …, F_n – равнодействующие внутренних консервативных сил, действующих на каждую из этих точек, а F₁, F₂, …, F_n – равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальную точку действуют еще и внешние неконсервативные силы. Равнодействующие их, действующие на каждую из материальных точек, обозначим f₁, f₂, …, f_n. При скоростях значительно меньших скорости света массы материальных точек будут постоянны, и уравнения II закона Ньютона будут иметь вид:

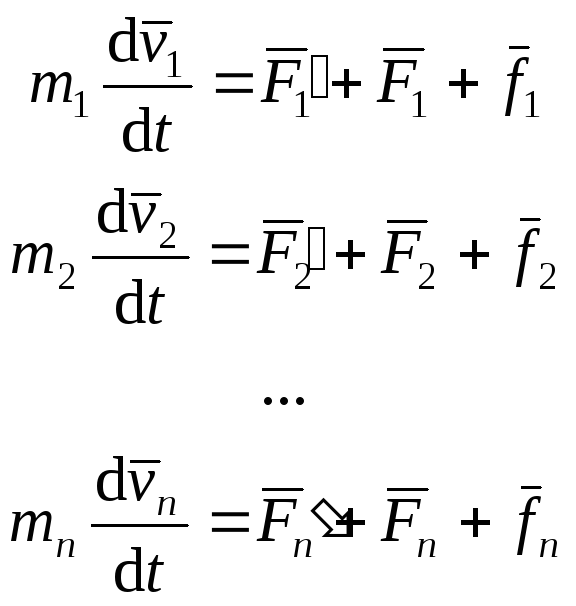
Двигаясь под действием этих сил, точки системы за интервал времени dt совершают перемещения, соответственно равные . Умножим каждое уравнение на величину перемещения, получим:

Сложим эти ур-ния и получим:

Первый член этого равенства даст изменение кинетической энергии.

Второе слагаемое равно элементарной работе внутренних и внешних консервативных сил взятой со знаком «–».

Правая часть равенства (1) задает работу внешних неконсервативных сил, действующих на систему. Таким образом,

d(Т + П)  = dA (2)

При переходе системы из состояния (1) в состояние (2) получают, что изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершаемой при этом внешними неконсервативными силами.

Если внешние неконсервативные силы отсутствуют, то d(Т + П)  = 0, Т + П = const (3)т.е. полная механическая энергия системы

сохраняется постоянно.Выражение (3) представляет собой закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы полная механическая энергия системы сохраняется, т.е. не изменяется со временем. Механические системы, на тела которых действуют только консервативные силы внутренние и внешние, называются консервативными системами.Тогда закон сохранения механической энергии можно записать так: в консервативных системах полная механическая энергия сохраняется.Закон сохранения механической энергии связан с однородностью времени. Однородность времени проявляется в том, что физические законы инвариантны относительно выбора начала отсчета времени. Например, при свободном падении тело в поле сил тяжести. Его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, когда это тело начало падать. Существует еще один вид систем – это диссипативные системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие механические формы энергии. Этот процесс получил название диссипации (рассеивания) энергии. Строго говоря, все системы в природе диссипативны. В консервативных системах закон сохранения механической энергии не просто закон сохранения в количественном смысле, а закон сохранения и превращения энергии, выражающий качественную сторону взаимного превращения различных форм движения друг в друга. Закон сохранения и превращения энергии – фундаментальный закон природы. Он справедлив как для систем макроскопических тел, так и для систем микро тел. В системе, где действуют также неконсервативные силы, полная механическая энергия не сохраняется, однако, при исчезновении механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь.В этом заключается физическая сущность закона сохранения и превращения энергии. Сущность неуничтожимости материи и ее движения. Графическое представление энергии Во многих задачах рассматривается одномерное движение тела, потенциальная энергия которого является функцией только одной переменной (например, координаты х), т.е. считается W_p(x). График зависимости потенциальной энергии от аргумента х называется потенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела.

В качестве примера рассмотрим зависимость W_p(x) на рис.1. Если полная энергия частицы равна W, то при условии выполнения закона сохранения энергии частица может находиться только там, где W_p  W, т.е. в областях II и IV. Из области II в область IV частица переходить не может, т.к. ей препятствует потенциальный барьер h . Для того, чтобы частица смогла преодолеть потенциальный барьер, ей необходимо сообщить дополнительную энергию, равную высоте барьера h (или превышающую ее). В области II частица с полной энергией W оказывается “запертой” в потенциальной яме ABC.