Вопрос 35: Кинематическое описание движения жидкости. Уравнение неразрывности.

Движение жидкостей называется течением. Совокупность частиц движущейся жидкости называется потоком. Линия тока - это линия, проведенная так, что касательная к ней совпадает по направлению с вектором скорости жидкости в соответствующих точках пространства. Часть жидкости, ограниченная линиями тока, называется трубкой тока.

Течение жидкости называют стационарным (установившимся) , если форма и расположение линий тока, а также скорости в каждой точке жидкости, со временем не изменяются.

Рассмотрим несжимаемую жидкость: ,s₁v₁ = s₂v_2. Это соотношение справедливо для любых сечений трубки, следовательно,

sv = const физический смысл произведения sv -объем жидкости, проходящей через сечение s за 1 с.

Вопрос 36: Ур-ние Бернулли и следствия из него. Давление в жидкости и газе.

Идеальная жидкость - это жидкость, в которой отсутствуют силы внутреннего трения .

Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения. В момент времени t жидкость заполняла участок ограниченный S₁ и S₂,

а в момент времени , она занимает объёми. В силу неразрывности струи заштрихованные объёмы будут иметь одинаковую величину.

По закону сохранения энергии: ;

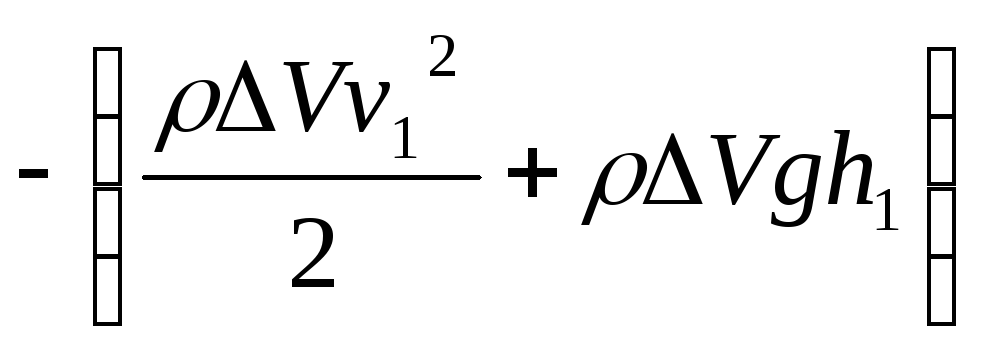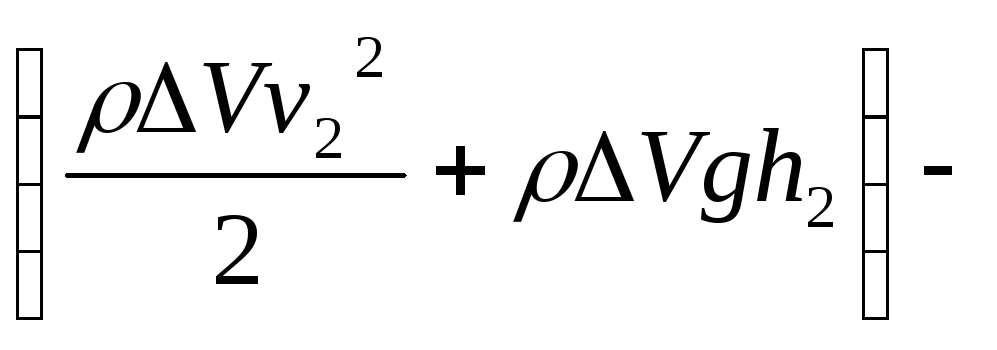
v₁²/2 + gh₁ + p₁ = v₂²/2 + gh₂ + p₂ ; или v²/2 + gh + p = const-

ур-ние Бернулли.

Уравнение Бернулли есть выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости.

Величину р называют статистическим давлением, величину v²/2 называют динамическим давлением, а величина gh являетсягидростатическим давлением.

Для горизонтальной трубки тока уравнение Бернулли имеет вид v²/2 + p = const, где величина v²/2 + p называется полным давлением. Из последнего уравнения и уравнения неразрывности следует, что при течение жидкости по горизонтальной трубке, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах.

Если жидкость неподвижна v=0, то p₁ и p₂=const и полное давление определяется гидростатическим и статическим давлением.

Вопрос 37: Силы внутреннего трения. Формула Стокса. Ламинарное и турбулентное течения жидкости.

Вязкость (внутреннее трение - это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

Силы внутреннего трения направлены вдоль соприкасающихся слоев и зависят от их относительных скоростей.

Ньютоном была установлена зависимость силы внутреннего трения от сопровождающих его явлений: F = |v/x|s, где v/x - градиент скорости (x - расстояние между двумя соседними слоями, v - разность скоростей жидкости в двух соседних слоях), s - площадь соприкосновения двух соседних слоев,  - коэффициент вязкости, зависящий от природы жидкости и температуры (единица вязкости - паскаль-секунда [Па^.с]: 1 Па^.с равен вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем 1м/с, возникает сила внутреннего трения 1 Н на 1 м² поверхности касания слоев (1 Па^.с = 1 Н^.с/м²).

 - коэффициент динамической вязкости;

- коэффициент кинематической вязкости в .

Ламинарное (слоистое) течение жидкости - когда вдоль потока каждый выделенный слой скользит относительно соседних, не перемешиваясь с ними. Этот режим наблюдается при небольших скоростях движения жидкости: внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным, а скорости последующих слоев тем больше, чем больше их расстояние до поверхности трубы и наибольшей скоростью обладает слой, движущийся вдоль оси трубы.

Турбулентное (вихревое) течение жидкости - когда вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости. При этом режиме течения частицы жидкости приобретают составляющие скоростей, перпендикулярные течению и поэтому они могут переходить из одного слоя в другой. Скорость частиц жидкости быстро возрастает по мере удаления от поверхности трубы, затем изменяется незначительно. Так как частицы жидкости переходят из одного слоя в другой, то их скорости в различных слоях мало отличаются. Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей.

Характер течения зависит от безразмерной величины - числа Рейнольдеса Re = <v>l/ , где- плотность жидкости, <v> - средняя по сечению трубы скорость жидкости,l- перемещение жидкости по оси x..

При Re < 1000 наблюдается ламинарное течение, в области 1000<Re<2000 происходит переход к турбулентном течению, а при Re > 2300 для гладких труб наблюдается турбулентное течение. Если число Рейнольдса одинаково, то режим течения различных жидкостей в трубах различных сечений одинаков.н

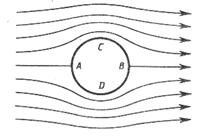для идеальной

жидкости

к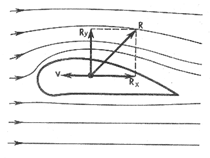рыло самолета

При движении тела в жидкости или газе с небольшими скоростями и малых Re сопротивление среды определяется силами трения и согласно Стоксу, эта сила пропорцианальна произведению динамической вязкости на линейные размеры тела и скорости движения тела в жидкости.

Если форма тела- шар, то сила сопротивления При движении падения шара в жидкости, то на него действуют: сила тяжести, выталкивающая сила и сила сопротивления в сторону противоположную движению. Когда силы выравниваются, то движение будет равномернымF₁ и F₂- постоянны; F₃ зависит от скорости.