
- •Вопрос1:Модели в механике. С о, траектория, длина пути, вектор перемещения, Кинем. Ур-ние движения мат. Точки.
- •2Вопрос: скорость и ускорение,угловая скорость и угловое ускорение.
- •2.Прямолинейное равноускоренное (равнопеременное) движение (равноускоренное или равнозамедленное):
- •Вопрос3: Первый закон Ньютона, мат. Запись, соврем. Трактовка, следствия из первого закона, инерциальные с о.
- •Вопрос4: II закон Ньютона, мат. Запись, соврем. Трактовка, следствия, усл-ия применимости, масса тела.
- •Вопрос5: III закон Ньютона, мат. Запись, соврем. Трактовка, силы трения.
- •Вопрос6: Закон сохранения импульса, вывод закона.
- •Вопрос7: Работа силы, мощность.
- •Вопрос8: Консервативные силы.
- •Вопрос9: Потенциальная энергия (вывод формулы).
- •Вопрос10: Энергия. Закон сохран. Энергии. Графич. Представление энергии.
- •Вопрос11: Применение з. С. Э. И з. С. И. К задаче об ударе упругих и неупругих тел.
- •Вопрос12: Движение твердого тела. Момент силы. Центр масс, закон движения центра масс.
- •Вопрос 13: Момент импульса. З.С.М.И. , вывод закона.
- •Вопрос 14: Момент инерции. Ур-ние динамики вращательного движ.(вывод).
- •Вопрос 15: Кинетическая энергия тв. Тела, совершающего вращательное движ.
- •Вопрос16: преобразования Галилея. Механический принцип относительности. Неинерциальная с о.
- •Вопрос17: Постулаты сто. Пробразования Лоренца.
- •Вопрос18: Следствия из преобразований Лоренца.
- •1.Одновременность событий в разных системах отсчета
- •2.Длительность событий в разных системах отсчета
- •3. Длина тел в разных системах отсчета
- •5.Четырехмерное пространство-время. Интервал между событиями.
- •Вопрос19: Основной закон релятивисткой динамики матер. Точки. Закон взаимосвязи массы и энергии.
- •Вопрос 20: Механические гармоническ. Колебания и их характеристики. Дифференциальное уравнение свободных гармонических колебаний (вывод).
- •Вопрос21: Механические гармонические колебания, кинетическая, потенциальная и полная энергия гармонического колебания (вывод).
- •Вопрос22: Гармонические осцилляторы:
- •Вопрос 23: Сложение гармонических колебаний одного направления и одинаковой частоты.
- •Вопрос 24: Сложение взаимно- перпендикулярных колебаний, фигуры Лиссажу.
- •Вопрос 27:Вынужденные гармонические колебания, дифференциальное ур-ние, его решение, резонанс.
- •Вопрос 28: Волновые процессы. Виды волн, монохроматическая бегущая волна, фазовая скорость.
- •Вопрос 29: Ур-ние плоской и сферической волн. Волновой вектор.
- •Вопрос 30: Волновое ур-ние(вывод). Скорость распространения волн в твердых телах, жидкостях и газах.
- •Вопрос 31: Поведение звука на границе раздела 2-х сред. Эффект Доплера в акустике.
- •Вопрос 32: Принцип суперпозиции. Групповая скорость. Интерференция волн. Стоячие волны.
- •Вопрос 33. Энергетические характеристики упругич волн, вектор Умова.
- •Вопрос 34:Понятие о сплошной среде. Общие св-ва газов и жидкостей.
- •Вопрос 35: Кинематическое описание движения жидкости. Уравнение неразрывности.
- •Вопрос 36: Ур-ние Бернулли и следствия из него. Давление в жидкости и газе.
- •Вопрос 37: Силы внутреннего трения. Формула Стокса. Ламинарное и турбулентное течения жидкости.
Вопрос 32: Принцип суперпозиции. Групповая скорость. Интерференция волн. Стоячие волны.
Линейная среда- среда, св-ва которой не изменяются под действием возмущений, создаваемых волной.
Если среда, в которой распространяются несколько волн, линейна, то к ним применим принцип суперпозиции (наложение) волн: при распространении в линейной среде нескольких волн, каждая из них распространяется так, как будто др. волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равного геометр. сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов, следовательно любая волна может быть представлена в виде суммы гармонических волн, т.е. в виде волнового пакета, или группы волн.
Волновым
пакетом- наз-ся суперпозиция волн, мало
отличающихся друг от друга по частоте,
занимающая в каждый момент времени
ограниченную область пространства.
«Сконструируем» простой волновой пакет
из двух продольных волн с одинаковыми
амплитудами, близкими частотами и
волновыми числами, причем
![]() и
и![]() ,
тогда
,
тогда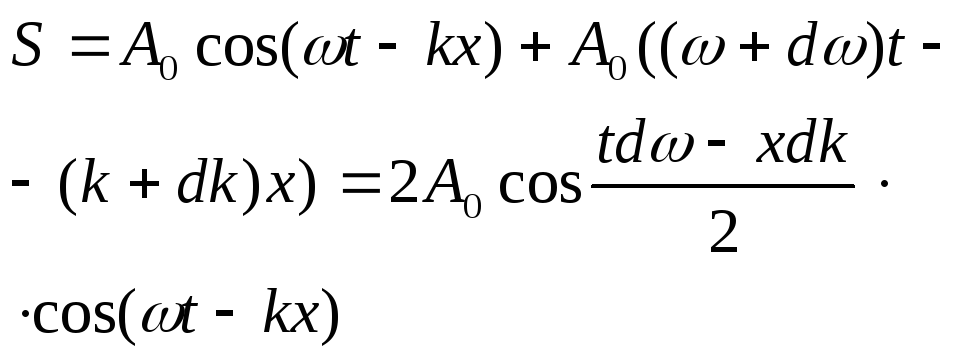
Эта
волна отличается от гармонической тем,
что ее амплитуда
![]() -
есть медленно изменяющаяся функция
координатx
от времени t.
-
есть медленно изменяющаяся функция
координатx
от времени t.
За
скорость распространения этой
негармонической волны (волнового пакета)
принимают скорость перемещения максимума
амплитуды волны, рассматривая тем самым
максимум в кач-ве центра волнового
пакета. При условии, что
![]() получим
получим![]() гдеu-
групповая скорость, которую можно
определить как скорость движения группы
волн, образующих в каждый момент времени
локализованный в пространстве волновой
пакет. Выражение (1) получено для волнового
пакета из 2-х составляющих, однако можно
док-ть, что оно справедливо в самом общем
случае.
гдеu-
групповая скорость, которую можно
определить как скорость движения группы
волн, образующих в каждый момент времени
локализованный в пространстве волновой
пакет. Выражение (1) получено для волнового
пакета из 2-х составляющих, однако можно
док-ть, что оно справедливо в самом общем
случае.
Рассмотрим
связь между групповой
![]() и фазовой
и фазовой
![]() скоростями, учитывая, что
скоростями, учитывая, что
![]() получим
получим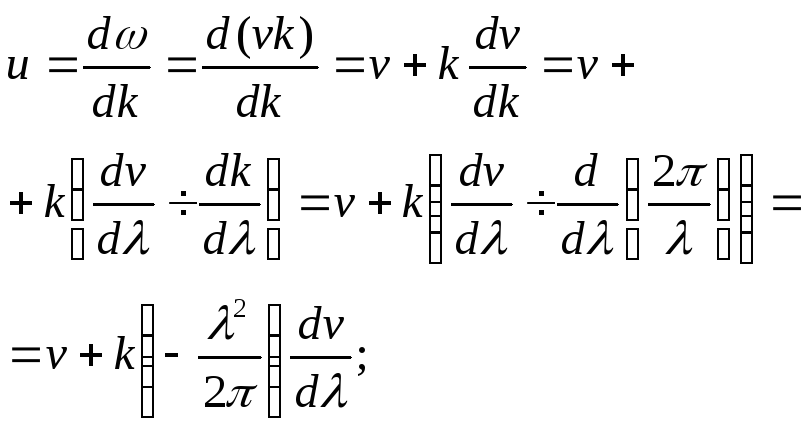 или
или![]() u
может быть> , или <v,
в зависимости от знака
u
может быть> , или <v,
в зависимости от знака
![]() ,
а в недиспергирующей среде
,
а в недиспергирующей среде![]() и
и![]() (фазе).
(фазе).
Интерференция волн.
Согласованное протекание во времени пространстве нескольких колебательных или волновых процессов связывают с понятием когерентности волн. Когерентными называют волны у которых разность фаз остается постоянной, могут быть лишь волны, имеющие одинаковую частоту.
Интерференция волн- явление усиления или ослабевания результирующей волны в зависимости от соотношения между фазами 2-х (или нескольких) когерентных волн при наложении этих волн в пространстве в разных его точках .
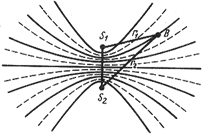
Рассмотрим
наложение 2-х когерентных сферических
волн, возбуждаемых точечными источниками
S1
и S2
(рис. 47)
колеблющимся с одинаковыми амплитудой
A0
и частотой
![]() и постоянной разностью фаз.
и постоянной разностью фаз.


![]()
![]()

Стоячие волны.
Стоячие волны- это волны, образующиеся при наложении 2-х бегущих , распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами, а в случае поперечных волн и одинаковой поляризацией.
Рассмотрим
2 плоские волны, распространяющиеся
навстречу друг другу вдоль оси х в среде
без затухания, причем А1=А2;
![]() ,
а в случае поперечных волн и с одинаковой
поляризацией. Начало координат выберем
в точке где обе имеют одинаковую начальную
фазу, а отсчет времени начнем с момента,
когда начальные фазы обеих волн равны
0. Тогда Ур-ния волны, распространяющейся
вдоль положительного направления оси
х и волны, распространяющейся ей
навстречу:
,
а в случае поперечных волн и с одинаковой
поляризацией. Начало координат выберем
в точке где обе имеют одинаковую начальную
фазу, а отсчет времени начнем с момента,
когда начальные фазы обеих волн равны
0. Тогда Ур-ния волны, распространяющейся
вдоль положительного направления оси
х и волны, распространяющейся ей
навстречу: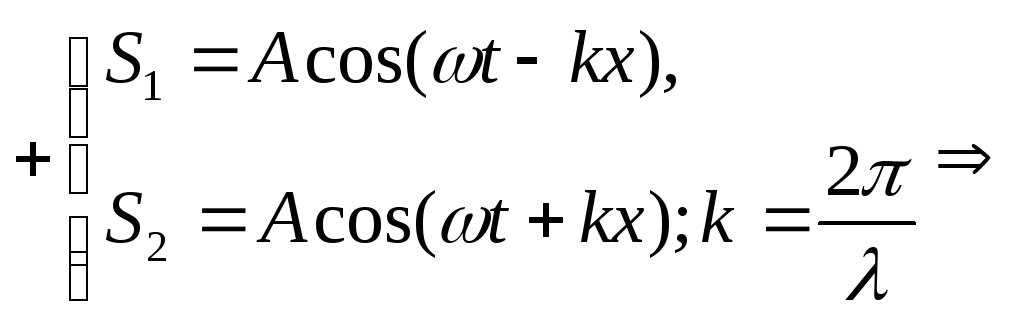
![]()
![]() зависит
от координаты х, рассматриваемой точки.
зависит
от координаты х, рассматриваемой точки.
