Министерство образования РФ

Рязанская государственная радиотехническая академия

Кафедра ОиЭФ

Лабораторная работа № 1-8

«ИЗУЧЕНИЕ СИЛ ВЯЗКОГО ТРЕНИЯ»

Выполнил ст. гр. 255

Ампилогов Н. В.

Проверил

Малютин А. Е.

Рязань 2002

Цель работы: изучение явления вязкого трения и одного из методов определения вязкости жидкости.

Приборы и принадлежности: Сосуд с жидкостью, шарики.

Элементы теории

При движении тел в жидкостях и газах на тела действуют силы вязкого трения. Явление вязкости тела относится к явлениям переноса. С точки зрения молекулярно –кинетической теории вязкость объясняется переносом импульса при взаимодействии молекул.

П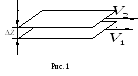ри ламинарном течении жидкости или газа между слоями, движущимися с различной скоростью, действуют силы, обусловленные вязкостью. Если два слоя площадью S (см. рис. 1) находятся на расстоянии Z и движутся с различными скоростями, так что V = V₂ – V₁, между ними возникает сила вязкого трения, которая пропорциональна градиенту скорости в направлении, перпендикулярном направлению течения, V/Z,

и площади слоёв S:

,

где коэффициент  - является вязкостью, или коэффициентом внутреннего трения (по определению).

Из данной формулы видно, что вязкость измеряется в Паскаль - секундах (Пас). Иногда используют и более мелкую единицу вязкости – пуа s (П): 1 Пас = 10 П.

Одним из метолов измерения вязкости вещества (вискозиметрии) является метод падающего шарика (метод Стокса). На шарик, движущийся в вязкой среде, действует сила вязкого трения, равная F = 3Vd, где V – скорость шарика; d – диаметр шарка.

Рассмотрим движение шарика при его падении, тогда уравнение второго закона Ньютона будет иметь следующий вид:

; где g – ускорение свободного падения; a – ускорение тела (в данном случае шарика); F_А – сила Архимеда; F – сила вязкого трения,

при ; имеем:

.

Силу Архимеда разложим следующим образом: ; при этом - сила тяжести шарика;  и _ж – плотности материалов шарика и жидкости соответственно.

Решением этого дифференциального уравнения будет следующая зависимость скорости от времени:

,

где V₀ начальная скорость движения шарика; - скорость установившегося движения (при t ).

Величина есть время релаксации. Эта величина показывает, насколько быстро устанавливается стационарный скоростной режим движения. Считается, что при t  3 режим движения практически не отличается от стационарного. Таким образом измерив скорость установившегося падения шарика в жидкости можно рассчитать её вязкость.

Условие ламинарности движения жидкости определяется значением безразмерного параметра – числом Рейнольдса:

R = _жVd/, где d – характерный размер движущегося тела (в данном случае – диаметр шарика). Формула Стокса справедлива при R < 1000. При R > 1000 движение становится турбулентным и формула Стокса неприменима.

Если тело, скорость которого измеряется, движется в достаточно узком цилиндре, то в расчётную формулу необходимо внести поправки на влияние стенок. В конечном виде формула для расчёта вязкости имеет следующий вид:

, где l – расстояние между стенками; D – диаметр внутренней части сосуда с жидкостью.

Р

№	dш10-3, м	t, с	, Пас
1	11,13	0,7	0,42
2	11,14	0,8	0,47
3	9,60	1,0	0,45

асчётная часть

После проведения всех необходимых замеров имеем значения следующих величин:

D = 5,3510^-2 м. (внутренний диаметр сосуда);

L = 0,5 м. (расстояние между метками);

_ж = 1,210³ кг/м³. (плотность жидкости);

_ш = 7,810³ кг/м³. (плотность шарика); с_м = 10^-5 м. (цена деления микрометра);

с_с = 10^-1 с. (цена деления секундомера).

Найдём действительные значения величин d и t (как среднее арифметическое).

м. с.

Теперь можно оценить погрешность результатов измерений:

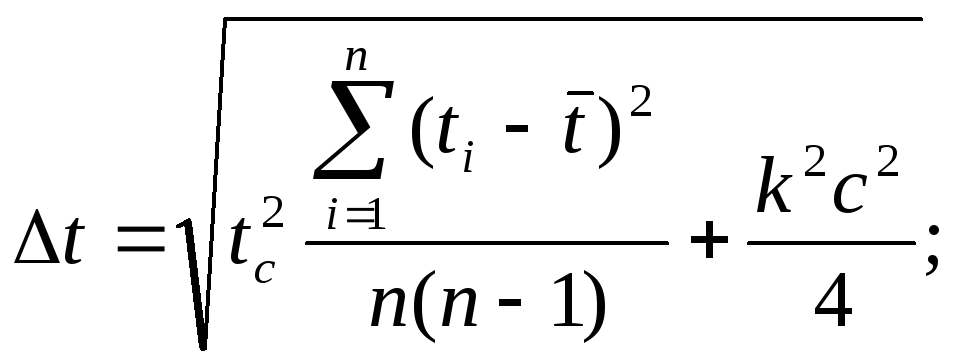
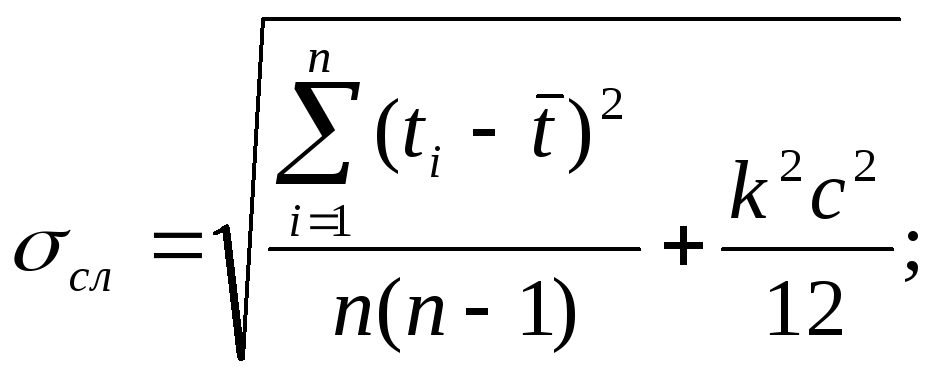t_c = 4,30 при n = 3, k =1,1 при P=0,95.

Следуя аналогичной последовательности вычислений найдём погрешности измерения d и t.

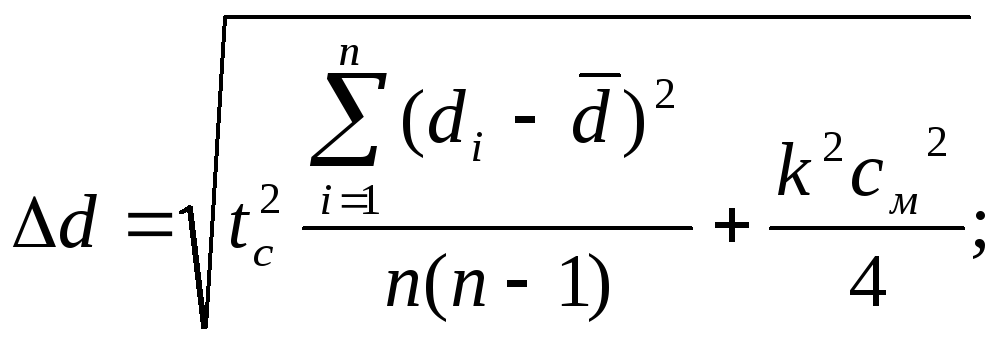
м.

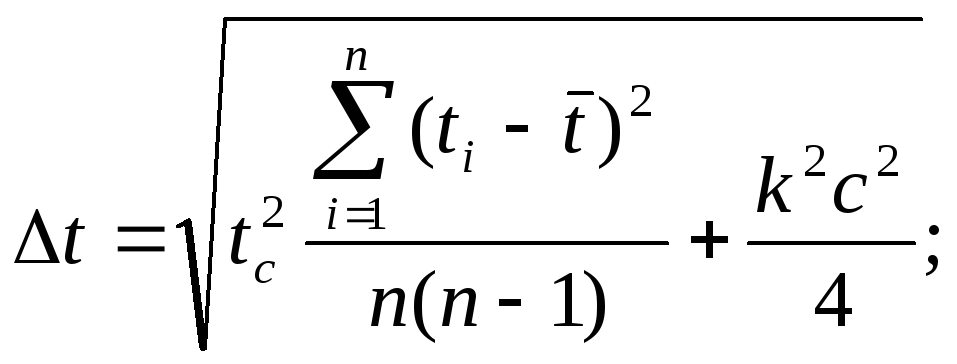
с.

По формуле найдём относительную погрешность для d и t.

; ;

Теперь по соответствующей формуле вычислим _i.

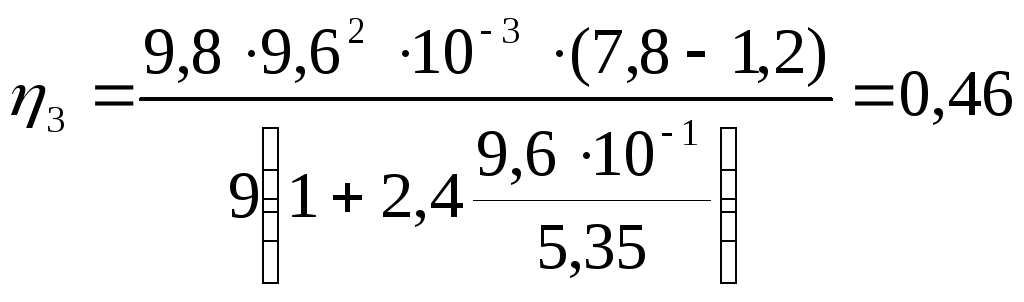Пас. Пас.

Пас.

Через данные 3 i-ых значения найдём действительную величину : Пас.

Далее вычислим по упрощённой формуле  и уже через относительную погрешность значения вязкости найдём её абсолютную погрешность .

; ;

Пас.

Теперь определим величину числа Рейнольдса, например, для 1-ого опыта.

; где ;; ;

Из полученного результата видно, что формула Стокса применима к данному случаю т.к. R<1000.

Вычислим время релаксации . ; с.

Из результата последнего вычисления получаем: . Следовательно, режим движения шарика в жидкости можно считать стационарным.

Вычислим S через следующую формулу, учитывая, что : S  2V.

; м.

 = 0,460,29 Пас.

- 4 -