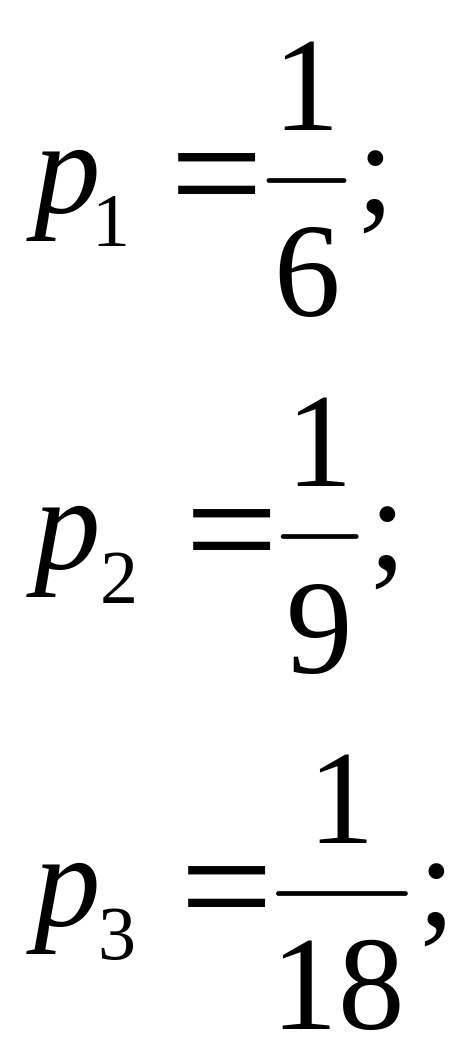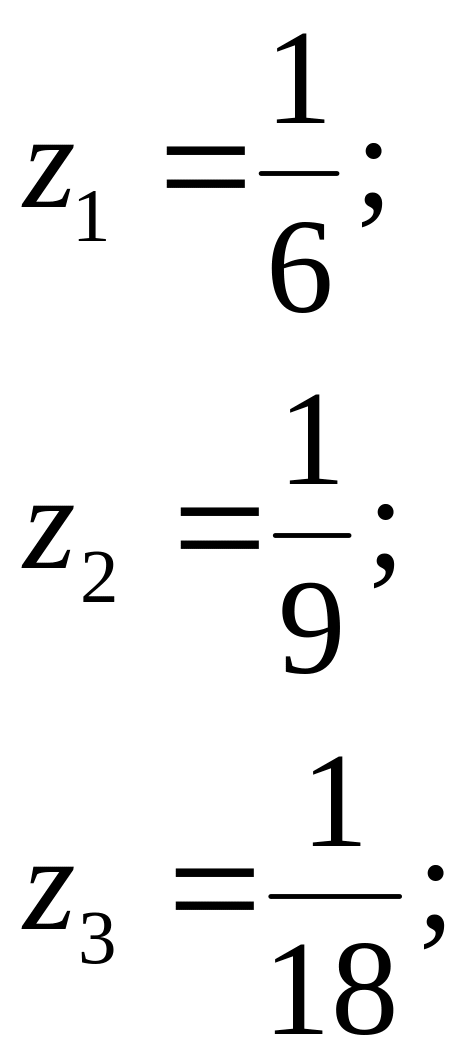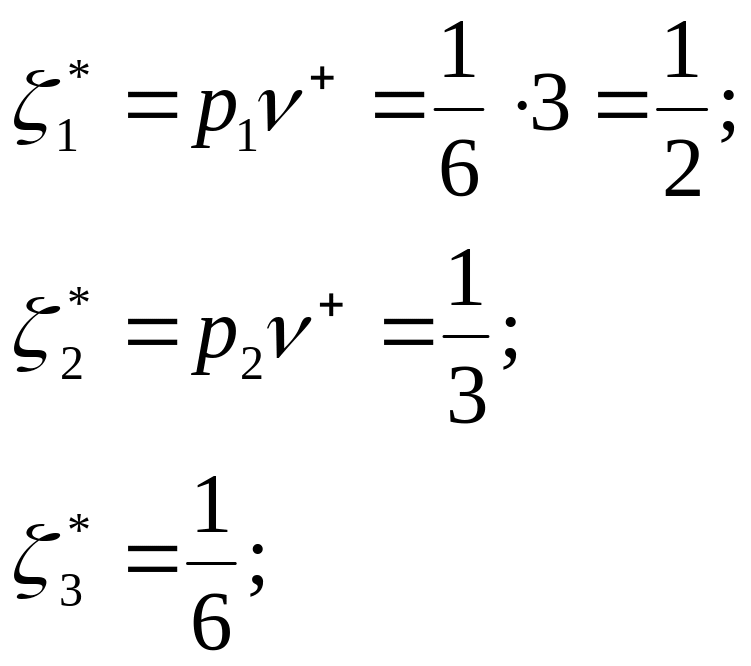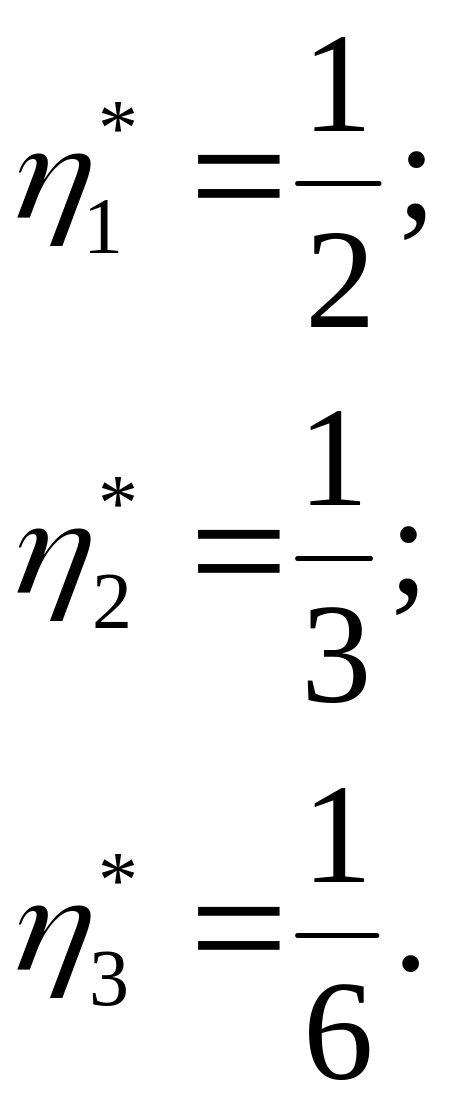1.5 Решение игр (m×n) методом линейного программирования

Теория игр находится в тесной взаимосвязи с линейным программированием (ЛП): любая конечная игра двух лиц может быть сведена к паре двойственных задач ЛП, и наоборот, задача ЛП может быть представлена как игра двух лиц. Таким образом, после сведения к игровой задачи к задаче ЛП можно применить любой известный метод (например симплекс-метод) и получить не приближенное, а точное решение игровой задачи.

Пусть дана игра . Будем считать, что в ней отсутствует седловая точка и удалены все доминируемые стратегии. Требуется найти точное решение. При m, n≥3 геометрическая интерпретация становится затруднительной.

Цена игры и оптимальные стратегии игроков могут быть определены путем сведения игровой задачи к паре двойственных задач ЛП.

Из свойств оптимальных стратегий следует, что если 1-й игрок использует оптимальную смешанную стратегию, а 2-й игрок использует любую из своих чистых стратегий , то

, j=1,…, n (1)

Кроме того , (2)

Аналогичные соотношения могут быть составлены и для 2-го игрока:

, i=1,…, m, (1*)

где . (2*)

Без ограничения общности будем считать, что цена игры , q_ij>0. Если в этом есть сомнения, то необходимо воспользоваться операцией приведения матрицы к виду без отрицательных элементов путем прибавления некоторой константы.

Разделим неравенства (1) и равенство (2) на цену игры ν и введем переменные p_i и z_j: .

После подстановки переменных в (1), (2) и (1*), (2*) получаем прямую и двойственную задачи ЛП следующего вида.

Прямая задача: , при условиях:

Двойственная задача: , при условиях:

Однако из теории ЛП известно, задача ЛП не всегда имеет решение, в отличие от конечной игры 2-х лиц с нулевой суммой (см. основную теорему теории игр). Следовательно, необходимо доказать, что в полученной паре двойственных задач всегда существует допустимое решение и целевая функция (ЦФ) является ограниченной.

Действительно, предположим, что в полученной задаче ЛП нет допустимого решения. Чтобы опровергнуть это, нужно указать на существование хотя бы одной точки в пространстве поиска решений, в которой все условия-ограничения выполняются. Какая это точка?

Поскольку все , то обозначим через . Тогда точка с координатами p₁ =1/ μ, р₂ = р₃ =…= р_m =0 является допустимым решением, т.к. она удовлетворяет условиям (2).

Целевая функция для прямой задачи ЛП минимизируется, поэтому она должна быть ограниченной снизу. В самом деле, все p_i ≥0, а коэффициенты в выражении (1) положительны, следовательно, целевая функция ограничена снизу нулем!

После сведения к задаче ЛП и ее решения любым известным методом, необходимо вернуться к исходной игровой задаче и определить цену игры и оптимальную стратегию игроков, исходя из следующих соотношений: , , ,

где i=1,…, m, j=1,…, n.

Рассмотрим пример. Найти решение игровой задачи следующего вида:

	0	1	-2
	-1	0	3
	2	-3	0

В матрице имеются отрицательные элементы, поэтому прибавляем ко всем элементам число 3 (цена игры увеличится на 3, на оптимальность стратегий операция не влияет):

	3	4	1
	2	3	6
	5	0	3

Пара двойственных задач будет выглядеть следующим образом:

прямая задача:

при условиях

двойственная задача:

при условиях

Составим симплекс-таблицу для прямой задачи (выбор зависит от того, какая из задач имеет меньшее число ограничений, что в свою очередь зависит от числа стратегий игроков) и приведем ее к каноническому виду (изменить знаки в строке целевой функции на обратные). Она будет иметь следующий вид:

				1
	3	2	5	-1
	4	3	0	-1
	1	6	3	-1
	-1	-1	-1	0

Разрешающий элемент для шага жорданова исключения выбираем исходя из известного условия: , причем ,

. Делаем шаг жорданова исключения с разрешающим элементом а₃₁, получаем следующую симплекс-таблицу:

				1
	3	-16	-4	2
	4	-21	-12	3
	1	-6	-3	1
	-1	5	2	-1

Найдено допустимое решение, поскольку выполняется условие о том, что все элементы столбца свободных членов должны быть неотрицательны.

Ищем оптимальное решение, выбирая в качестве разрешающего элемента элемент а₁₂ , найденный их условия: , причем , .

Выполняя шаг жорданова исключения, получим новую симплекс-таблицу:

				1
z2

				1

Оптимальное решение не достигнуто (все элементы строки ЦФ неположительны), поэтому выбираем новый разрешающий элемент, используя предыдущее условие (элемент а₂₃), делаем шаг жорданова исключения и получаем новую симплекс-таблицу, которая удовлетворяет условию оптимальности и одновременно является решением прямой и двойственной задачи ЛП. Из полученной таблицы следует, что цена игры

,