3.1. Классификация математических моделей в задачах принятия решений
Итак, ранее мы определили общую ММ ЗПР вид (3.1) - (3.3). В зависимости от природы и характера векторов a, b и c, входящих в эти выражения выделяют следующую классификацию ММ:
Рассмотрим краткую классификацию существующих моделей. По виду формального языка, применяемого при моделировании, выделяются аналитические модели, в которых для описания математических процессов применяется стандартная математическая символика (уравнения алгебраические и дифференциальные, логические операции и т.д.). Таким образом, эти ММ обычно представляются в виде формул.
Имитационные модели, в которых исследуемые процессы описываются на универсальных языках программирования, либо на специальных алгоритмических языках программирования типа GPSS.
По назначению ММ в науке и технике подразделяются на:
Расчетные модели и оптимизационные модели.
В ТПР в качестве ММ обычно используются оптимизационные модели. Расчетные модели могут быть использованы в качестве вспомогательного средства, используемого для обоснования и анализа оптимальных решений.
В качестве нового знания, которое получается в результате использования ММ и методов ТПР выступают оптимальные решения.
Детерминированные модели. В таких моделях числовые значения параметров a, b и c точно известны исследователю (ЛПР).
Стохастические. В этих моделях значения параметров a, b и c являются случайными векторами, заданными с помощью их функций распределения или числовых характеристик (математического ожидания, дисперсии). Задача оптимизации данного класса носит название задачи стохастического программирования.
Интервальные.
Используются в ЗПР с неопределенностью,
то есть в таких задачах, в которых векторы
,
,
могут быть описаны только множествами
их возможных значений. Например,
температура
может принимать значения в некотором
интервале, но закон ее распределения
неизвестен.
Для описания таких задач используется такое направление как интервальная арифметика, интервальный анализ. В последнее время появились методы решения задачи оптимизации, в которой параметры задаются в виде интервалов, в частности интервальное линейное программирование.
Математическая
модель (3.1) - (3.3) называется однокритериальной
моделью. Пусть ЛПР, должно учитывать
целей, в этом
случае используется
целевых функций:
,
(3.4)
Здесь
–
соответствующие вектора неконтролируемых
факторов. Математическая модель ЗПР
(3.4), (3.2), (3.3) называется многокритериальной
моделью.
В зависимости от
вида функций
и
,
входящих в соответствующую ММ, выделяют
линейные
и нелинейные
модели. В общем случае
линейная однокритериальная модель ЗПР
записывается в следующем виде:
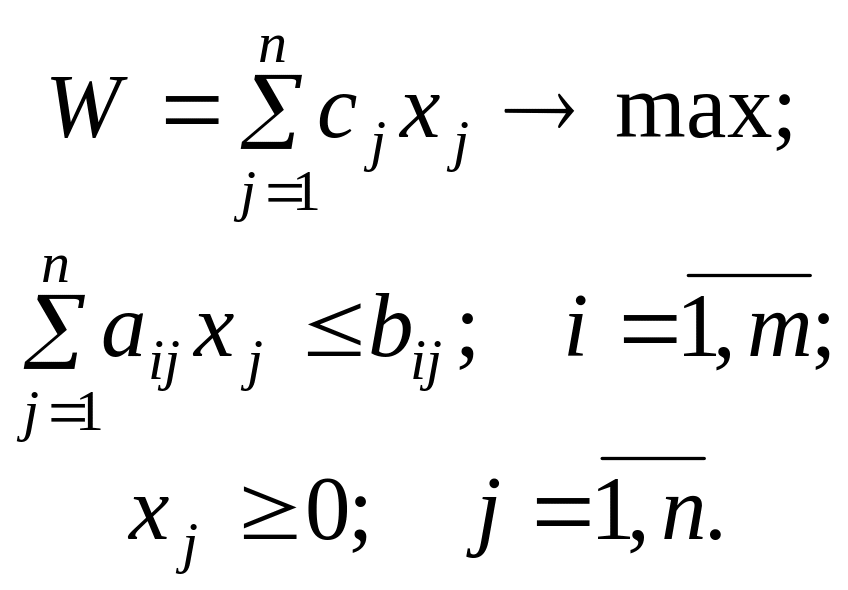(3.5)
Если модель не соответствует виду (3.5) по какой-то из компонент, то она относится к классу нелинейных моделей.
Если в модели учитывается ограничение (3.3) и вектора могут принимать только дискретный ряд значений, то это требование формально записывается так:
. (3.6)
Тогда модель (3.1),
(3.2), (3.6) называется однокритериальной
дискретной
моделью. А модель (3.4), (3.2), (3.6) –
многокритериальной дискретной моделью.
Модель называется смешанной
(дискретно-непрерывной),
если на одну часть компонент вектора
наложены условия не отрицательности
вида (3.3), а на другую – вида (3.6).
Таким образом, можно предложить следующую классификацию математических моделей задач принятия решений (рис. 3.1).
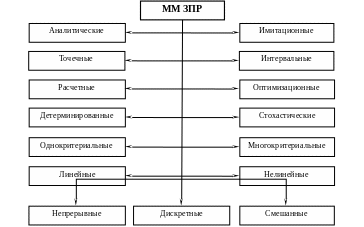
Рис. 3.1
В данном курсе будут рассматриваться аналитические, оптимизационные и далее по классификации ММ. Трудоемкость (вычислительная сложность) решения с их помощью соответствующих ЗПР увеличивается по правилу слева направо, то есть минимальные затраты машинного времени обычно тратятся при использовании детерминированной, однокритериальной, линейной модели.