5. Нелинейные модели задач принятия решений

Все рассмотренные выше ММ, являются линейными детерминированными моделями. В данном разделе будут рассмотрены примеры нелинейных моделей. Нелинейные модели обычно строятся с помощью двух подходов:

1) Использование закономерностей формул фундаментальных и прикладных наук.

2) Путем непосредственного вывода входящих в модель воздействий.

5.1. Задача о выборе геометрических размеров бака заданного объема

П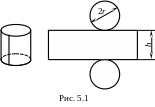 усть требуется выбрать геометрические размеры цилиндрического бака заданного объема V, из условия минимального расхода материала на его изготовление. Введем вектор проектных решений , где – радиус, h – высота бака. Будем считать, что бак изготовлен сваркой из трех деталей (рис. 5.1).

В этом случае расход материала при произвольном векторе решения x равен площади поверхности бака S

. (5.1)

Условие того, что бак должен иметь заданное значение объема:

. (5.2)

На компоненты вектора нужно наложить ограничения

, . (5.3)

Таким образом, выражения (5.1) - (5.3) описывают нелинейную однокритериальную модель задачи формирования оптимальных решений. Отметим, что данная модель была построена с использованием закономерностей элементарной геометрии. Если потребовать, чтобы бак имел минимальную трудоемкость его изготовления, а также предположить, что трудоемкость изготовления крышек и боковой стенки пренебрежимо малы (штамповка), то затраты времени на изготовление бака будут пропорциональны длине свариваемых швов.

, (5.4)

где  – затраты времени на сварку единицы длины шва. Выражения (5.4), (5.2), (5.3) также представляют собой однокритериальную нелинейную модель. Выражения (5.1), (5.4), (5.2), (5.3) описывают двухкритериальную нелинейную модель формирования оптимального проектного решения на бак.

Как было сказано выше, нелинейные модели в некоторых частных случаях допускают получение аналитического решения, то есть решения в виде формул. Построим аналитическое решение задачи (5.4), (5.2), (5.3), отбросив условие (5.3). Будем определять оптимальные значения r и h с помощью метода Лагранжа, применяемого в случае, когда все ограничения вида (3.2) имеют вид равенств:

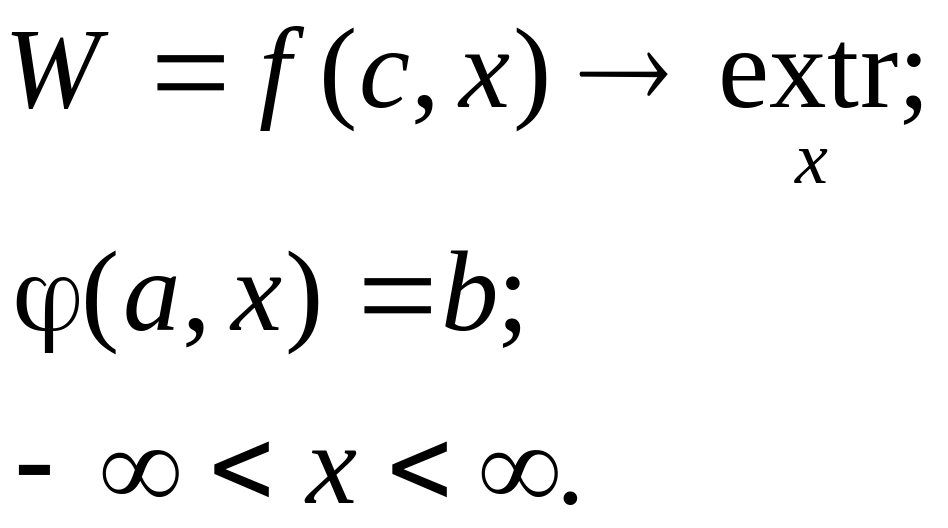
Функция Лагранжа имеет следующий вид:

где l₁, l₂, … , l_m – неопределенные множители Лагранжа.

Точки экстремума этой функции определяются из решения системы уравнений вида

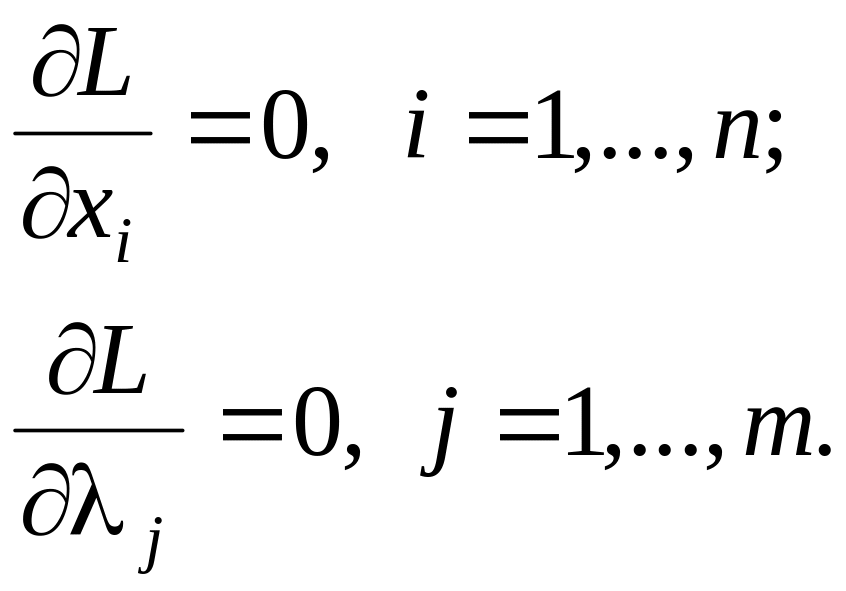
Решая эту систему, получим решение вида

Запишем функцию Лагранжа для задачи (5.4), (5.2):

,

Используя необходимое условие экстремума функции L, получаем систему уравнений для определения неизвестных h, и :

.

Оптимальное проектное решение имеет вид:

, .

Оптимальное решение не зависит от квалификации сварщика (), причем оптимальная высота бака равна длине его окружности:

.

5.2. Задача оптимального размещения предприятий

Пусть имеется два пункта потребления некоторого товара, на расстоянии друг от друга. Между этими пунктами требуется разместить предприятие, обеспечивающее выпуск единиц товара. Будем считать, что пункты потребления должны использовать весь товар в объеме . Известно, что стоимость перевозки единицы товара пропорциональна расстоянию от предприятия до пункта потребления.

Требуется определить точку размещения предприятия и объемы поставок товара каждому потребителю, так чтобы суммарные транспортные расходы были минимальными (рис. 5.2).

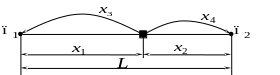
Рис. 5.2

Введенные переменные должны удовлетворять условиям:

(5.5)

(5.6)

Построим целевую функцию задачи. Стоимость перевозок единиц товара потребителям записывается как:

(5.7)

Здесь , – постоянные части стоимости перевозки единицы товара (например, з/п шофера, не зависящая от расстояния). Тогда стоимость перевозки всего объема произведенного товара вычисляется по формуле:

. (5.8)

Подставляя сюда выражения (5.7) получаем окончательный вид целевой функции:

. (5.9)

Получим нелинейную однокритериальную модель, которая описывается выражениями (5.9), (5.5), (5.6).

Решим поставленную задачу методом Лагранжа.

Функция Лагранжа имеет вид:

.

Возьмем частные производные по х₁, х₂, х₃, х₄, ₁, ₂:

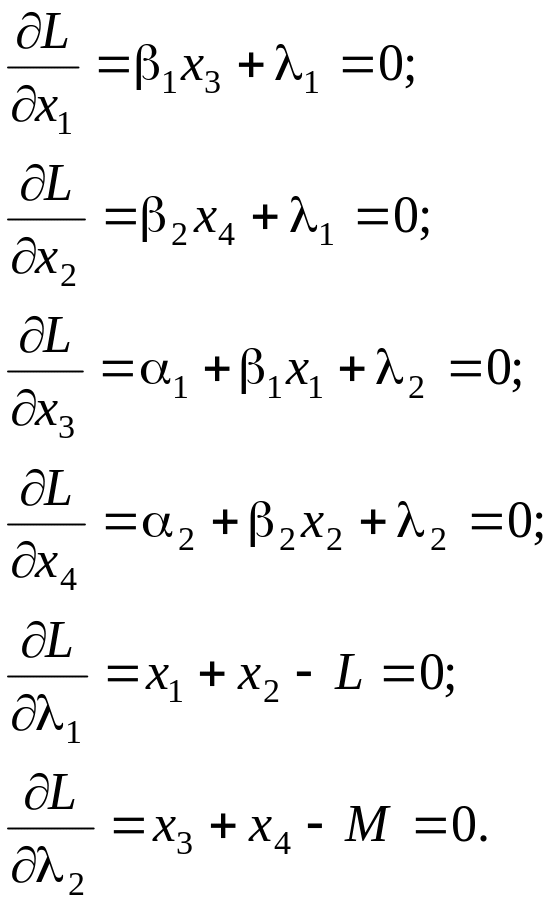
Решая полученную систему уравнений, получим:

, , , .