6.1. Решение двухкритериальной задачи о баке

Вернемся к задаче о баке (5.1), (5.4), (5.2), (5.3), описанной в п. 5.1:

;

;

;

, .

Построим линейную свертку критериев:

.

Функция Лагранжа запишется в виде

.

Распишем функцию Лагранжа подробнее:

.

Чтобы найти минимум функции Лагранжа, нужно взять от нее производные по искомым параметрам r, h, l и приравнять их к нулю.

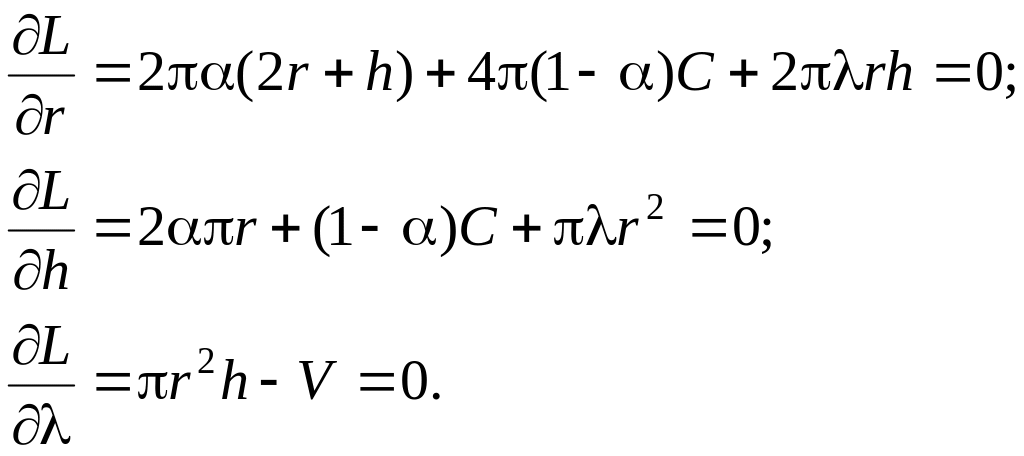(6.14)

Получили систему трех алгебраических уравнений, решив которую найдем зависимость r, h, l от a. Задавая a от 0 до 1, получим множество решений, оптимальных по Парето. Поскольку аналитически решить систему (6.14) довольно сложно, можно воспользоваться любым численным методом, задавая предварительно значения a с любым приемлемым шагом.

Задача была решена в пакете MathCad для V = 100 литров с шагом по  = 0,1. На рис. 6.4 показано полученное множество паретооптимальных решений.

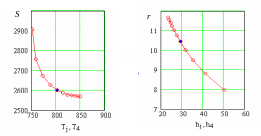
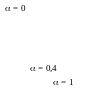
Рис. 6.4

ЛПР выбрал из этого множества точку при a = 0,4, при котором S = 2601; T = 802; r = 10,44; h = 29,2. Эта точка устроила его потому, что при дальнейшем увеличении a расход материала S уменьшается уже незначительно а трудоемкость Т имеет среднее – приемлемое значение.

6.2. Решение двухкритериальной стохастической задачи стоимости товаров в торговых центрах

Вернемся к задаче, описанной в п. 5.4 формулами (5.22), (5.24), (5.27), (5.26), (5.23). Для определения компромиссного значения цены х объединим задачи (5.22) и (5.26) в задачу максимизации векторного критерия вида

,

(6.15)

компоненты которого вычисляются по формулам:

; (6.16)

. (6.17)

В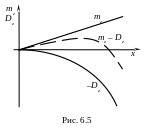 данной задаче у этих целевых функций отсутствует точка экстремума, однако, их свертка (6.15) имеет ярко выраженный максимум (рис. 6.5).

Отметим, что сформулированная задача относится к классу задач оптимального управления в среднем. В данной работе как развитие рассматривается многокритериальная оптимизация решений в среднем.

Построим линейную свертку критериев:

, (6.18)

где – параметр свертки.

Паретооптимальные решения задачи (6.18) будем формировать путем решения однокритериальной параметрической задачи оптимизации вида:

. (6.19)

Подставляя в формулу (6.18) выражения (6.16) и (6.17), имеем

.

Используя необходимые условия экстремума этой функции, получаем:

.

(6.20)

Значение второй производной

при и > 0 говорит о существовании максимума функции (6.18) в точке (6.20).

Удовлетворения ограничения (5.23) при решении задачи (6.15) будем добиваться путем использования в расчетах определенных значений параметра свертки . Подставляя выражение (6.20) в неравенство (5.23) и разрешая его относительно , получаем, что при использовании формулы (6.20) значения параметра  должны принадлежать интервалу , где

.

(6.21)

Построим оптимальные по Парето решения в пространстве критериев и . Подставляя (6.20) в выражения (6.16) и (6.17), имеем:

.

(6.22)

Исключая из этих выражений параметр , получаем в пространстве критериев зависимость вида:

, (6.23)

приведенную на рис. 6.6.

Д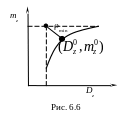 ля упрощения процесса принятия решения по цене в паретооптимальном множестве решений в пространстве критериев предлагается построить так называемую «идеальную» точку, не принадлежащую множеству эффективных точек. Координаты «идеальной» точки определяются из выражений

; .

Затем найти точку , наиболее «близкую» к «идеальной» точке , решив задачу

.

Таким образом, формирование паретооптимальных значений розничной цены на рассматриваемый товар осуществляется по следующему алгоритму:

1⁰. По заданным значениям , , и по формулам (6.21) вычисляются значения границ интервала варьирования параметра свертки .

2⁰. Формируется требуемая сетка значений этого параметра

.

3⁰. Для каждого значения , по формулам (6.20) и (6.22) вычисляются значения цены , среднего дохода и дисперсии дохода , таблица значений которых выдается ЛПР (маркетологу) для принятия решения по конкретному значению розничной цены в ТЦ.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Возможно ли получение единственного оптимального решения в многокритериальных задачах и почему?

2. Какие подходы обычно используют для решения многокритериальных задач?

3. Приведите общий вид двухкритериальной задачи.

4. Что такое множество достижимости?

5. Сформулируйте правило выделения лучших точек.

6. Что означает решения, оптимальные по Парето?

7. Приведите алгоритм нахождения оптимальных по Парето решений.

8. Приведите ММ двухкритериальной задачи о баке.

9. Приведите функцию Лагранжа для двухкритериальной задачи о баке.

10. Как найти минимум функции Лагранжа в двухкритериальной задаче о баке?

11. Запишите векторный критерий стохастической задачи стоимости товаров в торговых центрах с расшифровкой его компонент.

12. Запишите линейную свертку критериев в стохастической задаче стоимости товаров в торговых центрах.

13. Имеют ли экстремум целевые функции и их свертка в стохастической задаче стоимости товаров в торговых центрах?

14. Докажите, что точка, в которой производная от свертки равна нулю, является точкой максимума в стохастической задаче стоимости товаров в торговых центрах.

15. Какие значения может принимать параметр свертки в стохастической задаче стоимости товаров в торговых центрах?

16. Изобразите множество паретооптимальных точек в пространстве критериев для стохастической задачи стоимости товаров в торговых центрах.

17. Какой зависимостью она описывается?

18. Что такое идеальная точка, какие координаты она имеет в стохастической задаче стоимости товаров в торговых центрах?

19. Как определить расстояние от идеальной точки до любой точки паретооптимального множества в стохастической задаче стоимости товаров в торговых центрах?

20. Приведите алгоритм формирования паретооптимальных значений розничной цены на рассматриваемый товар.
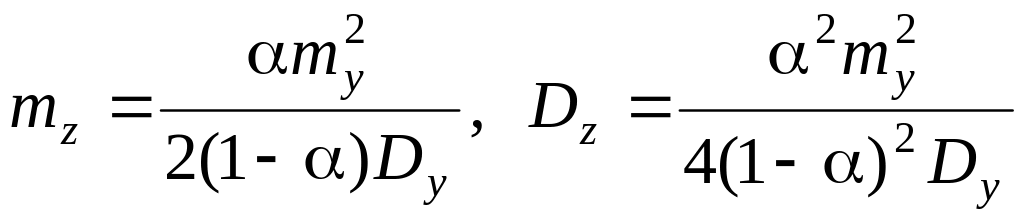