
- •П.И. Тутубалин, л.Т. Моисеева теория принятия решений
- •Оглавление
- •1. Основные понятия теории принятия решений 2
- •2. Классификация решений 5
- •4. Линейные модели задач принятия решений 16
- •5. Нелинейные модели задач принятия решений 42
- •6. Методы решения двухкритериальных задач принятия решений 53
- •1. Основные понятия теории принятия решений
- •2. Классификация решений
- •3. Общая математическая модель формирования оптимальных решений
- •3.1. Классификация математических моделей в задачах принятия решений
- •3.2. Краткая характеристика математических методов формирования оптимальных решений
- •4. Линейные модели задач принятия решений
- •4.1. Задача выбора оптимальной производственной программы предприятия
- •4.2. Распределительные задачи принятия решений
- •4.2.1. Задача распределения количества заказов по предприятиям
- •4.2.2. Задача распределения грузов по средствам доставки
- •4.2.3. Задача оптимизации перевозок однородного продукта
- •4.2.4. Метод минимальной стоимости для решения закрытой транспортной задачи
- •4.2.5. Задача о назначениях
- •4.3. Задача оптимального выбора
- •4.3.1. Задача о ранце
- •4.3.2. Задача оптимального выбора выполняемых работ
- •5. Нелинейные модели задач принятия решений
- •5.1. Задача о выборе геометрических размеров бака заданного объема
- •5.2. Задача оптимального размещения предприятий
- •5.3. Стохастическая модель выбора оптимальной производственной программы
- •5.4. Стохастическая модель стоимости товаров в торговых центрах
- •6. Методы решения двухкритериальных задач принятия решений
- •6.1. Решение двухкритериальной задачи о баке
- •6.2. Решение двухкритериальной стохастической задачи стоимости товаров в торговых центрах
- •Литература
5.3. Стохастическая модель выбора оптимальной производственной программы
Все рассмотренные выше задачи относились к детерминированным задачам принятия решений, то есть к задачам в которых , и были достоверно известны до решения задач. Существует класс задач, в которых эти параметры описываются случайными векторами. В этом случае соответствующие ММ относятся к классу стохастических задач. Рассмотрим одну из таких задач.
Рассмотренная выше классическая модель выбора оптимальной программы:
![]() ; (5.10)
; (5.10)
![]() ,
; (5.11)
,
; (5.11)
![]() ,
(5.12)
,
(5.12)
относится к классу
детерминированных моделей, так как
предполагалось, что все параметры
![]() ,
и
,
и
![]() не случайные величины. В реальности за
счет нестабильности в экономике и
действия в производственных процессах
всевозможных факторов эти параметры
могут рассматриваться как случайные
величины. В этом случае оптимальный
выбор производственной программы
необходимо осуществить с помощью
стохастических моделей.
не случайные величины. В реальности за
счет нестабильности в экономике и
действия в производственных процессах
всевозможных факторов эти параметры
могут рассматриваться как случайные
величины. В этом случае оптимальный
выбор производственной программы
необходимо осуществить с помощью
стохастических моделей.
Рассмотрим случаи, когда прибыль от реализации единицы продукции, запасы сырья и материалов являются случайными величинами.
Пусть значения
прибыли от реализации j-й
продукции
![]() являются случайными величинами. В этом
случае суммарная прибыль от реализации
продукции:
являются случайными величинами. В этом
случае суммарная прибыль от реализации
продукции:
![]() . (5.13)
. (5.13)
Максимизировать это выражение нельзя, так как в этом случае компоненты вектора решения х будут являться случайными величинами. Отметим, что при использовании любых стохастических моделей обязательно получение детерминированных компонент , учитывающих тот факт, что в задаче имеются случайные параметры. Будем считать, что из обработанной статистики нам известны математические ожидания и дисперсии случайных величин.
![]() ,
,
![]() ,
,
![]() .
.
Тогда критерий максимума средней прибыли записывается так:
![]() . (5.14)
. (5.14)
Здесь было использовано выражение (5.13), в котором все случайные величины были заменены их математическими ожиданиями (свойство линейной комбинации случайных величин). Теперь вид ММ определяют выражения (5.14), (5.11), (5.12).
Можно сформулировать
задачу выбора оптимального вектора
,
обеспечивающего минимальную дисперсию
суммарной прибыли (5.13). Для этого
используем следующее правило теории
вероятности. Пусть случайная величина
![]() вычисляется на основе коррелированных
случайных величин
вычисляется на основе коррелированных
случайных величин
![]() как сумма линейной комбинации
как сумма линейной комбинации
![]() ,
,
где
![]() –
неслучайные константы.
–
неслучайные константы.
Тогда дисперсия случайной величины вычисляется так:
![]() ,
,
где
![]() –
дисперсия случайной величины Yj.
–
дисперсия случайной величины Yj.
Применим это правило к выражению (5.13), где роль неслучайных параметров играют компоненты вектора , получаем:
![]() (5.15)
(5.15)
Таким образом, при случайных значениях прибыли можно решать двухкритериальную задачу (5.15), (5.14), (5.11), (5.12), обеспечивающую максимум средней прибыли и минимум ее дисперсии.
Рассмотрим случай,
когда случайным является объем ресурсов
входящих в условие (5.11). Пусть
![]() – случайные величины, описывающие эти
объемы.
В этом случае условие (5.11) становится
случайным неравенством вида:
– случайные величины, описывающие эти
объемы.
В этом случае условие (5.11) становится
случайным неравенством вида:
![]() ,
,
![]() . (5.16)
. (5.16)
Будем считать, что каждая случайная величина описывается ее функцией распределения:
![]()
![]() ,
. (5.17)
,
. (5.17)
Потребуем, чтобы неравенство (5.16) выполнялись с вероятностью близкой к единице. Это требование можно записать в виде
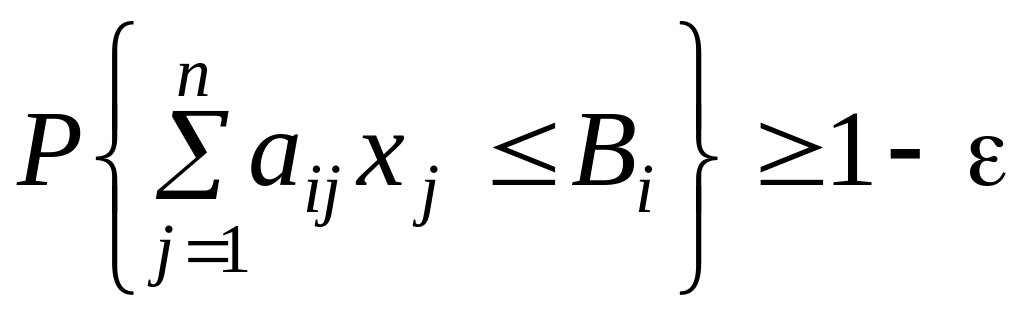 ,
,
![]() (5.18)
(5.18)
![]() –
достаточно малая
величина, которая в практических задачах
принимает значения 0,01; 0,05; 0,1. Из выражения
(5.17) следует, что вероятность
–
достаточно малая
величина, которая в практических задачах
принимает значения 0,01; 0,05; 0,1. Из выражения
(5.17) следует, что вероятность
![]() . (5.19)
. (5.19)
С учетом этого левую часть выражения (5.18) представим в виде
 .
.
Подставим полученное выражение в неравенство (5.18), получим
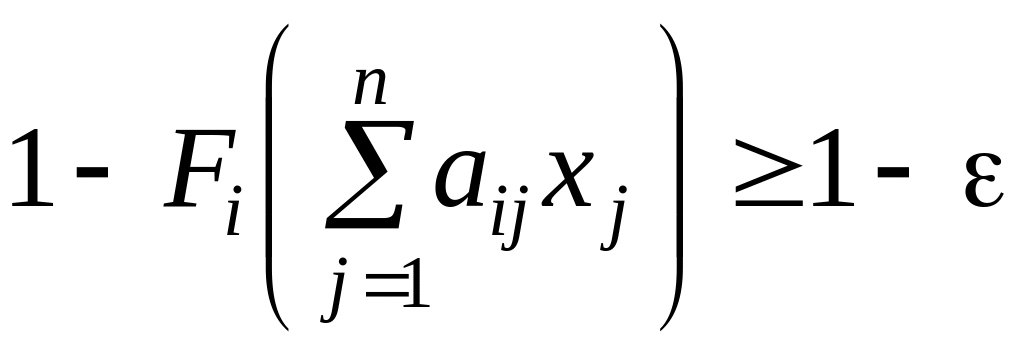 .
.
Приводя подобные члены и изменяя вид неравенств, получаем:
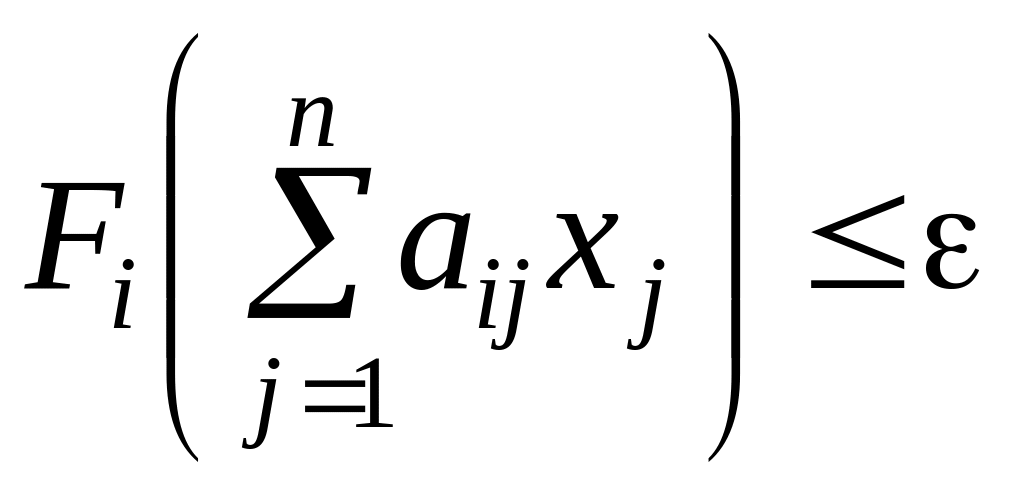 ,
,
![]() . (5.20)
. (5.20)
Таким образом, выражения (5.10), (5.20), (5.12) представляют собой стохастическую однокритериальную модель оптимальной производственной программы при случайной доступности ресурсов.
Рассмотрим пример,
когда все случайные величины
![]() распределены по равномерному закону в
соответствующих интервалах (рис. 5.3).
распределены по равномерному закону в
соответствующих интервалах (рис. 5.3).
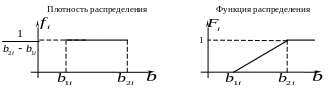
Рис. 5.3
![]()
С учетом этого неравенство (5.18) примет вид:
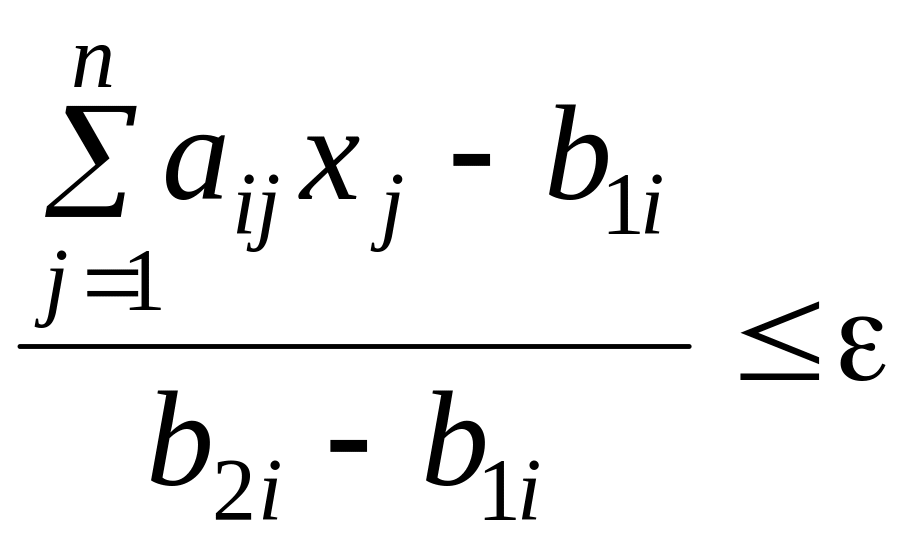
Проведя преобразования, имеем:
![]()
Эти линейные неравенства заменяют неравенства вида (5.16) в конкретных задачах ПР.
Построим конкретный
вид неравенства (5.16) для случая, когда
случайная величина
![]() распределена по показательному закону
с функцией распределения вида:
распределена по показательному закону
с функцией распределения вида:
![]() .
.
Согласно (5.20)
![]() .
Перенесем «единицу» в правую часть и
прологарифмируем обе части неравенства,
получим:
.
Перенесем «единицу» в правую часть и
прологарифмируем обе части неравенства,
получим:
![]() .
.
Отсюда:
![]() .
.
