4.2.5. Задача о назначениях

Пусть имеется работ и исполнителей (люди, оборудования и т.п.), которые могут выполнить любую из имеющихся работ, но должны быть назначены на выполнение одной и только одной работы. Требуется назначить конкретных исполнителей на выполнение конкретных работ так, чтобы эффективность их выполнения была максимальной.

Данная задача является частным случаем КТЗ при следующих значениях ее параметров: , , , .

Пусть известны величины эффективность выполнения -ой работы -м исполнителем (например, производительность). Требуется провести назначение имеющихся исполнителей заданным работам так, чтобы суммарная эффективность была максимальна. Построим ММ данной задачи, рассмотрев три возможных случая.

1) , 2) , 3) .

Введем в рассмотрение булевские переменные

, , . (4.33)

При этом, если в результате решения получим , то на -ю работу направляется -й исполнитель. При такое направление не производиться. Исходя из свойства условий (4.33), суммарная эффективность выполнения всех работ всеми исполнителями записывается как:

. (4.34)

Это выражение является целевой функцией данной задачи, которая в конкретной ЗПР должна быть либо максимальна ( – производительность), либо минимальна ( – общее время или общая стоимость выполнения всех работ).

Рассмотрим различные частные случаи ММ.

1) . В этом случае имеют место условия:

каждая работа должна иметь своего одного исполнителя:

, ; (4.35)

каждый исполнитель должен быть назначен на одну работу:

, . (4.36)

При решении необходимо найти значение переменных , удовлетворяющих условиям (4.33), (4.35), (4.36) и доставляющих критерию оптимальности (4.34).

2) . Число выполняемых работ больше, чем число исполнителей. В этом случае часть работ не выполнима, но все исполнители должны быть загружены выполнением своих работ.

, ; (для m – n значений i ) (4.37)

, . (4.38)

Математическая модель ЗПР в данном случае определяется выражениями (4.34), (4.33), (4.37), (4.38).

3) . Здесь все работы должны иметь своих исполнителей, но часть исполнителей (n – m) будет «безработными». Эти факты формализуются следующим образом:

, ; (4.39)

, . (для m – n значений j ) (4.40)

Модель задачи оптимального назначения в данном случае определяется следующими выражениями (4.34), (4.33), (4.39), (4.40).

Рассмотренные выше модели относятся к классической постановке задачи о назначениях, в которой используется один критерий.

На практике возникают многокритериальные задачи о назначениях. Рассмотрим пример одной из таких задач, в которой в качестве критериев оптимальности принятия решений выступают:

1. Суммарные затраты на обучение исполнителей.

2. Суммарная прибыль от выполнения всего комплекса работ.

Введем обозначения: – затраты средств на обучение -го исполнителя на выполнение i-й работы, – прибыль от выполнения i-й работы j-м исполнителем. Тогда критерии оптимальности запишутся как:

(4.41)

Таким образом, мы получим двухкритериальные задачи о назначении:

1. (4.41), (4.33), (4.35), (4.36);

2. (4.41), (4.33), (4.37), (4.38);

3. (4.41), (4.33), (4.39), (4.40).

Пример №1. Пусть имеется три вида земляных работ и три экскаватора для их выполнения. Производительность каждого экскаватора при выполнении каждого вида из земляных работ приводится в таблице:

Работы Экскаваторы	1	2	3
1	50	75	24
2	31	19	46
3	15	14	32

Требуется назначить экскаваторы на такие работы, чтобы суммарная производительность была максимальной.

Критерий оптимальности запишется следующим образом:

,

где х_ij означает – i-й экскаватор выполняет j-ю работу.

Ограничения – все экскаваторы заняты на всех работах:

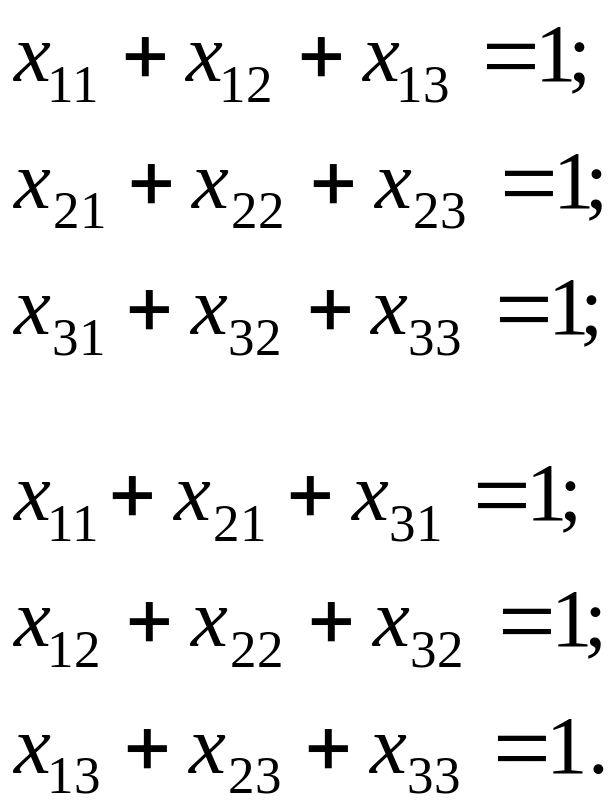
В результате получено оптимальное решение

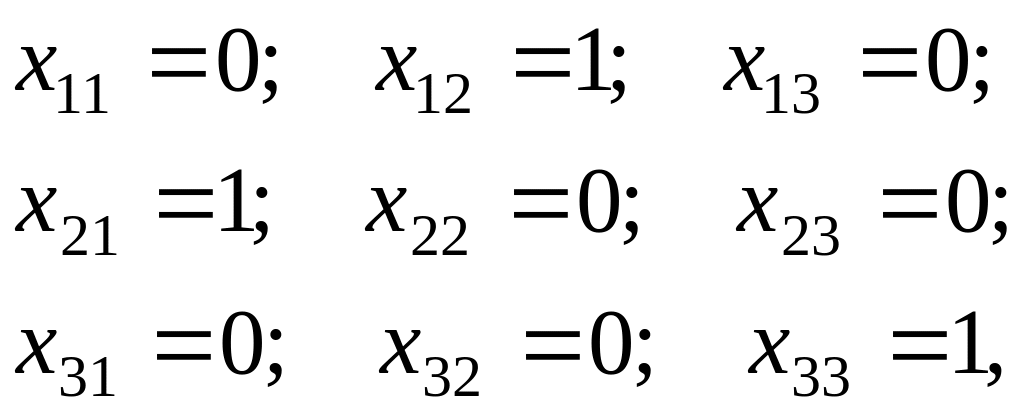
при котором целевая функция имеет максимальное значение:

Р_max = 75 + 31 + 32 = 138.

Рассмотрим случай, когда три экскаватора должны выполнить две работы (т = 2, п = 3), то есть в ходе решения задачи необходимо выяснить, какой экскаватор оставить без работы, а оставшиеся 2 выгодно распределить на 2 работы.

Критерий оптимальности в этом случае запишется следующим образом:

.

Ограничения – все работы обеспечены экскаваторами:

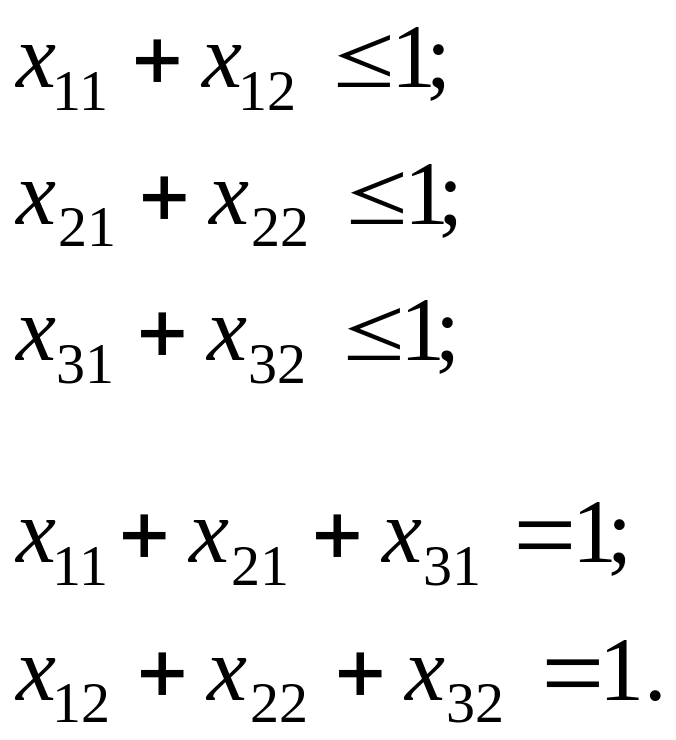
В результате получено оптимальное решение

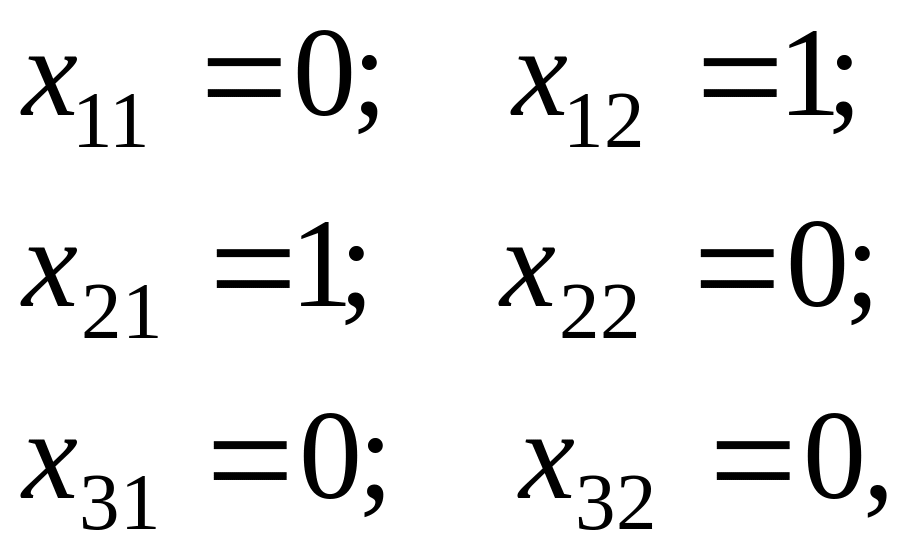
при котором целевая функция имеет максимальное значение:

Р_max = 75 + 31 = 106.

Рассмотрим случай, когда два экскаватора должны выполнить три работы (т = 3, п = 2), то есть в ходе решения задачи необходимо выяснить, какая работа останется не выполненной, и какими экскаваторами будет выполнена каждая из оставшихся 2-х работ.

Критерий оптимальности запишется следующим образом:

.

Ограничения – все экскаваторы обеспечены работой:

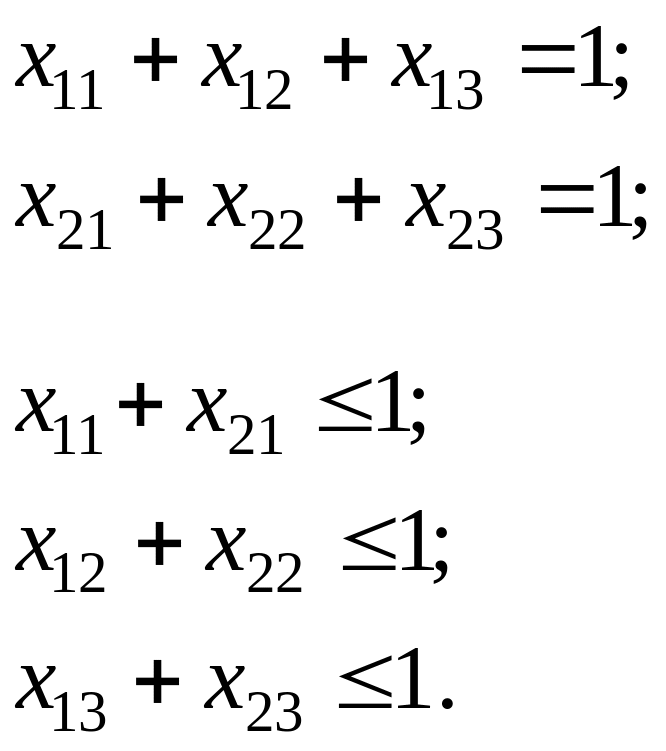
В результате получено оптимальное решение

при котором целевая функция имеет максимальное значение:

Р_max = 75 + 46 = 121.

Пример №2. Пусть в некоторый момент времени на станцию скорой медицинской помощи (СМП) поступает вызовов. На дежурстве в данный момент времени имеется бригад (машин СМП). Требуется провести оптимальное назначение бригад на полученные вызовы, обеспечивающие минимальные затраты времени на перемещение ко всем больным всех бригад.

Пусть для каждого i-го вызова и каждой j-й бригады с использованием электронной карты города определены расстояния , которые должны пройти j-я машина к i-му больному. Далее с использованием АСУ дорожного движения города получают фактические значения скоростей ( ) движения автотранспорта для всей совокупности маршрутов.

Тогда суммарные затраты времени на приезд бригад к местам вызовов определяются как

. (4.42)

В зависимости от соотношения чисел m и n в каждый момент времени могут использоваться ограничения:

а) (4.35) и (4.36) при m = n;

б) (4.37) и (4.38) при m > n;

в) (4.39) и (4.40) при m < n.

Практическое решение в каждый момент времени может быть различным в зависимости от соотношения m и n, а также различных значений параметров и .