§3. Поток векторного поля

Пусть в области задано некоторое векторное поле F i j k, где , , – непрерывно дифференцируемые в области функции. Пусть – гладкая ориентируемая поверхность, на которой выбрана определенная сторона, задаваемая единичной нормалью n к этой поверхности.

Потоком векторного поля F через поверхность S в направлении единичной нормали n называют поверхностный интеграл первого рода:

П .

(1)

Поверхностный интеграл первого рода в формуле (1) связан с поверхностным интегралом второго рода равенством:

П ,

(2)

которое дает еще один способ вычисления потока.

Физический смысл потока: если вектор-функция F есть поле скоростей текущей жидкости, то поток П этого векторного поля через поверхность S общему количеству жидкости, протекающей через S за единицу времени.

Формула Гаусса-Остроградского

Теорема (Остроградский). Пусть – замкнутая гладкая ориентируемая поверхность, являющаяся границей тела и n – единичная внешняя нормаль к . Пусть векторное поле F – непрерывно дифференцируемо на и в V. Тогда

.

(3)

Выражение, стоящее под знаком интеграла в правой части равенства (3), представляет собой дивергенцию векторного поля F, интеграл, стоящий слева, представляет собой поток векторного поля F через поверхность в направлении внешней нормали. Поэтому формула (3) может быть переписана в виде:

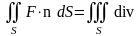F .

Формулу Гаусса-Остроградского часто применяют для вычисления потока векторного поля через замкнутую поверхность . Однако следует иметь в виду, что для применения этой формулы необходимо, чтобы векторное поле было непрерывно дифференцируемым внутри поверхности . Это условие всегда будет выполнено, если область , в которой рассматривается поверхность , пространственно односвязная.

Область называется пространственно односвязной, если из того, что замкнутая поверхность лежит в , следует, что тело V, границей которого является поверхность , тоже лежит в .

Пример 1. Вычислить поток векторного поля F через поверхность в сторону, определяемую вектором единичной нормали n к поверхности , если:

1. F , а – часть плоскости , расположенная в октанте , , , n образует острый угол с осью ;

2. F , – часть плоскости , расположенная в октанте , , , а n образует острый угол с осью ;

3. F , – часть параболоида , удовлетворяющая условию , а n – внешняя нормаль к параболоиду.

Решение. а) Нормальным вектором к плоскости является вектор, координаты которого суть коэффициенты при неизвестных в уравнении плоскости. В нашем случае – это вектор m . Поскольку m·F , то нормаль m к плоскости, (а значит, и единичная нормаль n к этой плоскости) перпендикулярна векторному полю. Но тогда

.

б) Вычислим поток векторного поля с помощью поверхностного интеграла второго рода (формула(2))

П

(в нашем случае ). Для вычисления последнего интеграла изобразим на чертеже поверхность (рис. 39) и ее проекцию на плоскость (рис. 40).

Рис. 39

Рис. 40

Нормаль n к плоскости , образующая острый угол с осью , образует тупой угол с осью (это видно из чертежа; однако несложно показать, что нужную сторону поверхности задает единичная нормаль n ; здесь , а , следовательно, и образует острый угол с осью и тупой – с осью ). Поэтому при сведении поверхностного интеграла к двойному по области перед двойным интегралом необходимо поставить минус:

П

в) Изобразим поверхность вместе с требуемой в условии задачи нормалью на рис. 41.

Из геометрических соображений понятно, что единичная нормаль n (т. к. она – внешняя нормаль) образует тупой угол с осью . Также ясно, что она образует острый угол с осью в тех точках, где и тупой – в тех, где 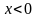. Аналогично, n образует острый (тупой) угол с осью в точках, где выполняется неравенство 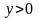( ). Для вычисления потока векторного поля напишем интеграл второго рода:

П .

Вычислим каждый из трех интегралов отдельно. Для вычисления интеграла

разобьем поверхность на две части: и плоскостью 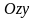( отвечает той части параболоида, где ). Необходимость разбиения заключается, в том что нормаль n на образует острый угол с осью (т.е. 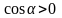), а на – тупой. Проекцией и и на плоскость является одна и та же область , показанная на рис. 42. Следовательно,

.

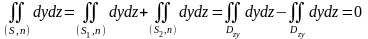Рис. 41

Рис. 42

Знак минус перед вторым интегралом поставлен так как на нормаль образует тупой угол с осью (т.е. 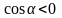). Из соображений симметрии понятно, что и

.

Осталось вычислить

.

Как отмечено выше, . Поэтому имеем:

,

где – проекция поверхности на плоскость (она изображена на рис. 43). Для вычисления последнего интеграла перейдем к полярным координатам:

.

Рис. 43

Таким образом, поток векторного поля равен .

Контрольные вопросы:

1. Дайте определение потока векторного поля F через поверхность .

2. Приведите формулу Гаусса-Остроградского.