
Задания для самостоятельного решения:
1. Вычислить следующие криволинейные интегралы первого рода:
а)
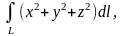 - дуга цепной линии
,
,
- дуга цепной линии
,
,
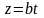 ,
;
,
;
б)
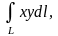 - четверть эллипса
- четверть эллипса
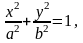 ,
.
,
.
2. Найти координаты центра тяжести дуги циклоиды , , .
3. Вычислить массу:
а)
четверти эллипса
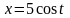 ,
,
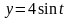 ,
расположенную в первой четверти, если
ее линейная плотность
,
расположенную в первой четверти, если
ее линейная плотность
 равна у.
равна у.
б)
контура прямоугольника со сторонами,
лежащими на прямых
,
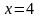 ,
,
,
,
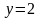 ,
если
,
если
 ;
;
в)
дуги параболы
,
заключенной между точками О(0,0)
и
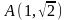 ,
если
.
,
если
.
4. Вычислить площади цилиндрических поверхностей, ограниченных снизу плоскостью , а сверху поверхностью , при условии, что известна направляющая этой цилиндрической поверхности:
а)
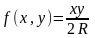 ,
;
,
;
б)
 ,
,
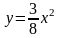 (
(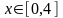 ).
).
5. С помощью криволинейного интеграла первого рода найти координаты центра тяжести кривых:
а)
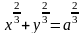 ,
;
,
;
б)
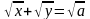 (
(![]() ).
).
6. Вычислить криволинейный интеграл:
а)
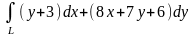 ,
,
по
разным путям, соединяющим точки
 ,
,
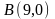 ,
,
 :
:
1) - отрезок ОА;
2) - ломаная ОВА;
3) - ломаная ОСА;
4) - парабола, соединяющая точки и и симметричная относительно оси .
5) проверить выполнение условия Грина.
б)
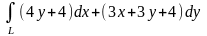
по
разным путям, соединяющим точки
,
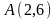 ,
,
 ,
:
,
:
1)
 ;
;
2)
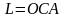 ;
;
3)
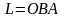 ;
;
4)
- дуга
параболы
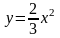 .
.
в)
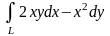 ,
,
взятый
вдоль различных путей, соединяющих
точки
,
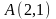 ,
,
,
,
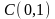 :
:
1) - отрезок ОА;
2) - парабола с осью симметрии , проходящая через точки О и А;
3) - парабола, проходящая через точки О и А с осью симметрии ;
4) - ломаная ОВА;
5) - ломаная ОСА.
7. Вычислить:
а)
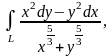 где
- дуга кривой
где
- дуга кривой
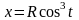 ,
,
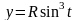 ,
пробегая от точки
,
пробегая от точки
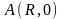 к
к
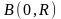 .
.
б)
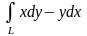 ,
где линия L
– задана уравнениями
,
где линия L
– задана уравнениями
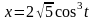 ,
, ,
, .
.
в)
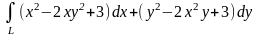 ,
где L
– дуга параболы
,
соединяющей точки
,
где L
– дуга параболы
,
соединяющей точки
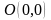 и
и
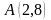 .
.
8. Вычислить криволинейные интегралы:
а)
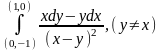 .
.
б)
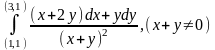 .
.
9. Применяя формулу Грина, вычислить криволинейные интегралы:
а)
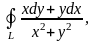 где
- окружность
где
- окружность
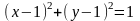 ,
пробегаемая против часовой стрелки.
,
пробегаемая против часовой стрелки.
б)
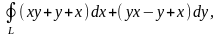 - эллипс
.
- эллипс
.
10. Найти работу силы:
а)
F=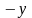 i+
i+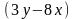 j
при перемещении материальной точки
вдоль контура прямоугольника с вершинами
,
j
при перемещении материальной точки
вдоль контура прямоугольника с вершинами
,
 ,
,
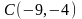 ,
,
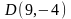 .
.
б) F= i+ j при перемещении материальной точки вдоль эллипса
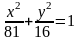 .
.
11. Вычислить поверхностные интегралы первого рода:
а)
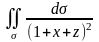 ,
где часть плоскости
при условии
,
,
.
,
где часть плоскости
при условии
,
,
.
б)
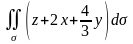 ,
часть плоскости
,
часть плоскости
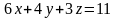 ,
лежащая в первом октанте.
,
лежащая в первом октанте.
в)
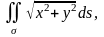 где
- боковая поверхность конуса
где
- боковая поверхность конуса
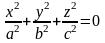 (
(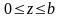 ).
).
12. Вычислить следующие интегралы второго рода:
а)
 где у – внешняя сторона тетраэдра,
ограниченного плоскостями
где у – внешняя сторона тетраэдра,
ограниченного плоскостями
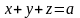 ,
,
,
.
,
,
,
.
б)
 где
- внешняя сторона эллипсоида
где
- внешняя сторона эллипсоида
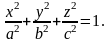
в)
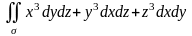 ,
где
у – внешняя сторона сферы
,
где
у – внешняя сторона сферы
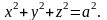
13. Найти поток вектора:
а)
F
i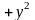 j
k
через поверхность тела
j
k
через поверхность тела
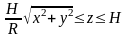 в
направлении внешней нормали.
в
направлении внешней нормали.
б)
F
2xi-yj
через
часть поверхности цилиндра
,
,
,
 в направлении внешней нормали.
в направлении внешней нормали.
14. Найти массу поверхности:
а)
куба
,
,
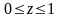 ,
если поверхностная плотность в каждой
точке
,
если поверхностная плотность в каждой
точке
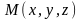 равна
равна
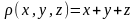 .
.
б)
куба
,
,
,
если поверхностная плотность в каждой
точке
равна
 .
.
Сыктывкарский государственный университет
