
§2. Криволинейный интеграл второго рода
Определение криволинейного интеграла второго рода
Пусть
на кривой
определены две ограниченные функции
 и
и
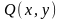 .
Разобьем кривую
на
п
равных частей точками
.
Разобьем кривую
на
п
равных частей точками
 ,
,
 ,
…,
,
…,
 ,
,
 ,
…,
,
…,
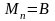 .
На каждой из полученных дуг
возьмем произвольную точку
.
Обозначим через
.
На каждой из полученных дуг
возьмем произвольную точку
.
Обозначим через
 и
и
 проекции дуги
на оси координат. Затем составим
интегральную сумму для функции
[
]:
проекции дуги
на оси координат. Затем составим
интегральную сумму для функции
[
]:


Пусть d – наибольшая из длин дуг . Если функция ( ) непрерывна в точках кривой , то при существует предел интегральных сумм, не зависящий от способа разбиения кривой на части и выбора точек . Этот предел называется криволинейным интегралом второго рода от функции [ ] по кривой и обозначается


Сумму криволинейных интегралов

называют полным криволинейным интегралом второго рода.
Криволинейный интеграл второго рода обладает теми же свойствами, что и определенный интеграл. В частности,
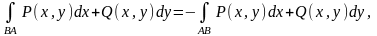
т. е. криволинейный интеграл второго рода меняет знак при изменении направления интегрирования.
Вычисление криволинейных интегралов второго рода
Предположим, что кривая задана в явном виде непрерывно дифференцируемой функцией , . Тогда

Если задается параметрическими функциями , , , то

Это
равенство можно распространить и на
пространственный случай (аргументы
 функций P,
Q,
R
для краткости опускаем):
функций P,
Q,
R
для краткости опускаем):

где , , , - параметрические уравнения кривой .
Приложения криволинейного интеграла второго рода
Интеграл

можно представить в виде скалярного произведения векторов F=Pi+Qj и ds=i·dx+j·dy:
 .
.
В таком случае

выражает
работу переменной силы F=Pi+Qj
при
перемещении материальной точки
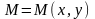 вдоль кривой
от точки А
до точки В.
вдоль кривой
от точки А
до точки В.
При А= В кривая замкнута, а соответствующий криволинейный интеграл по замкнутой обозначается так:
 .
.
В этом случае направление обхода контура поясняется стрелкой на кружке, расположенном на знаке интеграла.
Предположим,
что в плоскости
имеется односвязная область
 ,
ограниченная кривой
,
ограниченная кривой
 (
( -обозначение
границы области
),
а в области
и на границе
функции
и
непрерывны вместе со своими частными
производными.
-обозначение
границы области
),
а в области
и на границе
функции
и
непрерывны вместе со своими частными
производными.
Теорема.
Пусть А
и В
– произвольные точки области
,
 и
и
 - два произвольных пути (гладкие кривые),
соединяющие эти точки (рис. 32). Тогда
следующие условия равносильны:
- два произвольных пути (гладкие кривые),
соединяющие эти точки (рис. 32). Тогда
следующие условия равносильны:
1.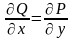 (условие
Грина).
(условие
Грина).
2.
 (криволинейный интеграл не зависит от
пути интегрирования).
(криволинейный интеграл не зависит от
пути интегрирования).
3.
 (интеграл по любому замкнутому пути
равен нулю).
(интеграл по любому замкнутому пути
равен нулю).
4.
 (выражение
(выражение
 представляет собой полный дифференциал
некоторой функции
представляет собой полный дифференциал
некоторой функции
 ).
).

Рис. 32.
В
случае выполнения любого из равносильных
условий теоремы криволинейный интеграл
по любой кривой, соединяющей точки
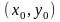 и
и
 из области
,
можно вычислить при помощи формулы
Ньютона – Лейбница
из области
,
можно вычислить при помощи формулы
Ньютона – Лейбница
 ,
,
где
 - некоторая первообразная для
может быть найдена при помощи криволинейного
интеграла
- некоторая первообразная для
может быть найдена при помощи криволинейного
интеграла
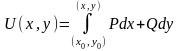 .
.
В этих же условиях на функции и , а также на область , имеет место формула Грина, позволяющая свести криволинейный интеграл по замкнутому контуру к двойному интегралу
 .
.
Считаем, что обход границы области в криволинейном интеграле

совершается в положительном направлении, т.е. при таком обходе границы область остается слева; для односвязной области это направление совпадает с направлением против часовой стрелки.
Также
площадь
 области
может быть вычислена при помощи
криволинейного интеграла второго рода:
области
может быть вычислена при помощи
криволинейного интеграла второго рода:
 .
.
Пример
1.
Даны функции
 ,
,
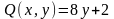 и точки
и точки
 ,
,
 ,
,
 .
Вычислить криволинейный интеграл
.
Вычислить криволинейный интеграл
 ,
,
где:
1) - отрезок ОА;
2) - ломаная ОВА;
3) - ломаная ОСА;
4) - парабола, симметричная относительно оси и проходящая через точки О и А;
5) проверить выполнимость условия Грина.

Рис. 33.
Пути интегрирования, соответствующие пунктам 1) – 4), изображены на рис.33.
1)
Отрезок ОА
может быть записан в виде:
 ,
,
 .
Тогда
.
Тогда
 и
и
 .
.
2)
Используем свойство аддитивности,
вычисляя отдельно интеграл по отрезкам
 и
и
 .
Тогда:
.
Тогда:
а)
:
здесь
,
 ,
т.е.
,
т.е.
 ,
откуда
,
откуда

б)
:
 ,
,
 ,
т. е.
,
т. е.
 ,
и
,
и

Таким образом,

3) Этот интеграл вычислим аналогично предыдущему.
а)
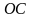 :
,
(т. е.
),
,
откуда
:
,
(т. е.
),
,
откуда
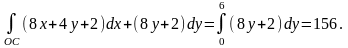
б)
 :
,
:
,
 ,
,
следовательно,
,
,
следовательно,

Окончательно

4)
Подставим координаты точки
в равенство
 найдем уравнение данной параболы
найдем уравнение данной параболы
 При этом
и
При этом
и
 ,
откуда (путь ОА
по параболе обозначим
,
откуда (путь ОА
по параболе обозначим
 )
)

5) Имеем
 ,
,
 ,
,
т. е. условие Грина не выполняется. Вычисления в пунктах 1) – 3) этой задачи показывают, что данный криволинейный интеграл второго рода зависит от пути интегрирования.
Пример 2. Вычислить интеграл
 ,
,
где
- верхняя половина эллипса
 ,
пробегаемая по ходу часовой стрелки.
,
пробегаемая по ходу часовой стрелки.
Воспользуемся
параметрическими уравнениями эллипса:
,
 ,
,
 ,
т. е.
,
т. е.
 ,
,
 .
Подставляя в интеграл и учитывая
направление обхода (откуда следует, что
меняется от π
до
0), получаем
.
Подставляя в интеграл и учитывая
направление обхода (откуда следует, что
меняется от π
до
0), получаем
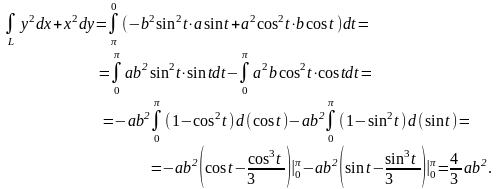
Пример 3. Вычислить

по
дуге винтовой линии
 при изменении
от 0 до
при изменении
от 0 до
 .
.
Сначала
найдем дифференциалы переменных:
 .
.
Выразим подынтегральное выражение через , сводя исходный интеграл к
определенному:

Пример 4. Показать, что интеграл

не
зависит от пути интегрирования,
соединяющего точки
 и
и
 ,
и вычислить его.
,
и вычислить его.
Проверим
условие Грина. Положим
 ,
, .
Тогда
.
Тогда
 ,и,
значит, данный интеграл действительно
не зависит от пути интегрирования. Для
вычисления данного интеграла в качестве
пути интегрирования возьмем отрезок,
соединяющий точки O
и B
.
Отрезок OB
можно задать так:
,
,и,
значит, данный интеграл действительно
не зависит от пути интегрирования. Для
вычисления данного интеграла в качестве
пути интегрирования возьмем отрезок,
соединяющий точки O
и B
.
Отрезок OB
можно задать так:
, .
При этом
.
При этом
 ,
и интеграл легко сводится к определенному
интегралу.
,
и интеграл легко сводится к определенному
интегралу.
 .
.
Пример 5. Вычислить криволинейный интеграл
 ,
,
где
L
– отрезок, соединяющий точку
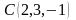 с
точкой
с
точкой
 .
.
Составим параметрические уравнения отрезка CD, используя уравнения прямой, проходящей через две точки:

Отсюда
 ,
,
 ,
,
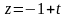 ,
,
 .
Далее, находим
.
Далее, находим
 ,
,
 ,
,
 ,
подставляем все нужные выражения в
данный интеграл, обозначенный через J,
и вычисляем определенный интеграл:
,
подставляем все нужные выражения в
данный интеграл, обозначенный через J,
и вычисляем определенный интеграл:

Пример 6. Проверить, является ли выражение

полным дифференциалом некоторой функции и если да, то найти эту функцию.
Обозначим
 .
Тогда
.
Тогда
 .
.
Таким
образом, условие Грина
 имеет место при
имеет место при
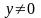 .
.
Следовательно, данное выражение есть полный дифференциал некоторой функции , которая может быть найдена как криволинейный интеграл
 ,
,
где
- произвольная фиксированная точка
плоскости
,
не лежащая на оси
(так как
 ).
Положим
).
Положим
 ,
а в качестве пути интегрирования выберем
путь
,
а в качестве пути интегрирования выберем
путь
 ,
изображенный на рис. 34.
,
изображенный на рис. 34.
Тогда сокращенно можно написать


Рис. 34.
Имеем:
1)
 ,
т.е.
и
,
т.е.
и
 .
.
2)
 :
- фиксировано, следовательно,
,
откуда
:
- фиксировано, следовательно,
,
откуда
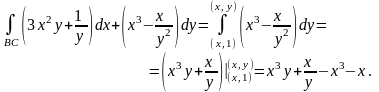
3)
Таким образом,

Проверка показывает, что действительно,

Пример 7. С помощью формулы Грина преобразовать криволинейный интеграл

в
двойной и с его помощью вычислить
интеграл по контуру прямоугольника
 (рис.35), где
(рис.35), где
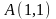 ,
,
 ,
,
 ,
,
 .
.

Рис. 35.
Имеем
 ,
,
 ,
откуда
,
откуда


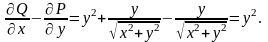
Таким
образом, в силу формулы Грина данный
интеграл равен двойному интегралу от
 по прямоугольнику
,
т. е.
по прямоугольнику
,
т. е.
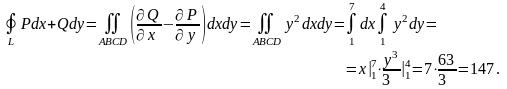
Пример 8. Вычислить площадь эллипса при помощи криволинейного интеграла.
Запишем эллипс в параметрической форме , , , после чего воспользуемся формулой для площади области

Пример 9. Вычислить работу силового поля F=yi – xj при перемещении материальной точки вдоль верхней половины эллипса
из
точки
 в точку
в точку
 .
.
Работа
 силового поля F=Pi+Qj
при
перемещении материальной точки
силового поля F=Pi+Qj
при
перемещении материальной точки
 вдоль
линии
вдоль
линии
 равна
равна
 .
.
Запишем дугу эллипса в параметрической форме: , , . Тогда , и
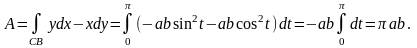
Контрольные вопросы:
Дайте определение криволинейного интеграла второго рода от функции .
Что называется полным криволинейным интегралом второго рода?
Зависит ли криволинейный интеграл второго рода от пути интегрирования?
Приведите формулу Грина.
