Рекомендуемая литература:

Основная литература.

1. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии: Учебное пособие для втузов/ Под ред. Гордона В.О. и Иванова Ю.Б. – 24-е изд.-М.: Высш. шк., 2009. - 272с.

2. Волошин-Челпан. Э. К. Начертательная геометрия. Инженерная графика. Издательство: Академический Проект; 2009 г. – 296с.

3. Нартова л. Г., Якунин в. И.. Начертательная геометрия. –м.: Академия, 2011.

4. Фролов с. А. Начертательная геометрия. – m.: Издательство: Инфра-м, 2011.

5. Чекмарев А.А. Начертательная геометрия и черчение. - М.: Юрайт, 2011. – 335с.

Дополнительная литература

6. Макарова М.Н., Начертательная геометрия.– М.: Академический Проект, 2008. – 395 с.

7. Короев Ю.И. Начертательная геометрия. – М.: КноРус, 2011г. – 252с.

8. Короев Ю.И. Сборник задач по начертательной геометрии. Учебник. Питер, 2008г. – 320с.

9. Буланже г. В., Гущин и. А., Стогнев а. Д. Основы начертательной геометрии. Методика решения типовых позиционных и метрических задач, Издательство: Высшая школа; 2010 г.- 208с

10. Фролов С.А. Сборник задач по начертательной геометрии. Учебное пособие. - 3-е изд. – СПб.: Лань, 2008г. - 192с.

11. Бударин О.С. Начертательная геометрия. Учебное пособие. 2-е изд. – СПб.: Лань, 2009г. – 368с.

12. П. Г. Талалай. Компьютерный курс начертательной геометрии на базе КОМПАС-3D (+ DVD-ROM). Спб. - БХВ-Петербург; 2010 г.- 520с.

Периодические издания:

1. Прикладная геометрия, инженерная графика, компьютерный дизайн за 2010 – 2011 год

2. Сапр и графика за 2010-2011г.

КОНТРОЛЬНЫЕ РАБОТЫ

Контрольная работа №1

Лист 1

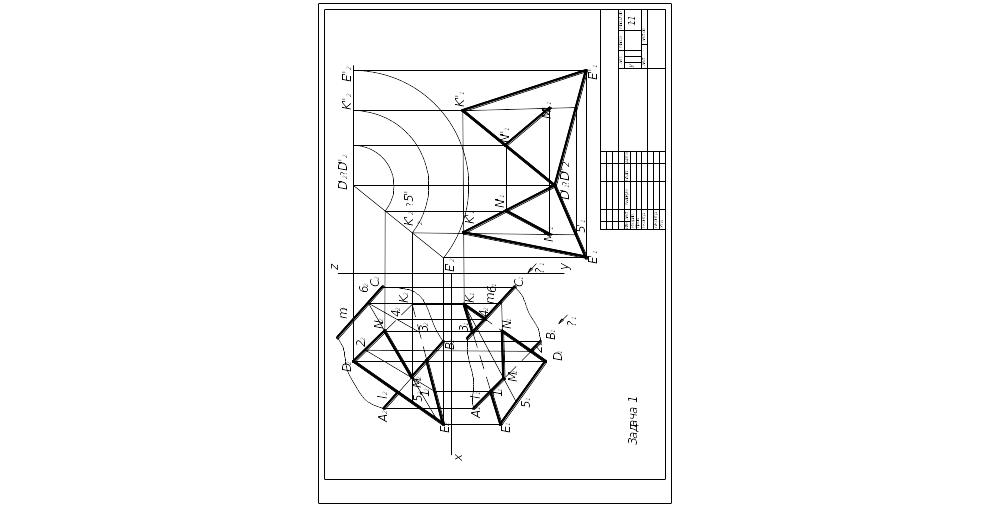
Задача 1. Построить линию пере­сечения плоскости α заданной треугольником EDK и плоскости β заданной параллельными прямыми l и m, и показать видимость их в проекциях. Определить натуральную величину треугольника EDK. Данные для своего варианта взять из табл. 1. Пример выполнения листа 1 приведен на рис. 1.

Указания к решению задачи 1. В левой половине листа формата A3 (297X420 мм) намечаются оси коор­динат и из табл. 1 согласно своему варианту берутся координаты точек А, В, С, D, Е, К. Через точки А и В проходит прямая l, через точку С - прямая m. (рис. 1). Стороны треугольни­ков и другие вспомогательные прямые проводятся вначале тонкими сплош­ными линиями. Линии пересечения плоскостей строятся по точкам пе­ресечения сторон треугольника с прямыми l и m или по точкам пересече­ния. Такую линию можно построить, используя и вспомо­гательные секущие проецирующие плоскости.

Видимость сторон треугольника оп­ределяется способом конкурирующих точек. Видимые отрезки линий выделяют сплошными жир­ными линиями, невидимые следует показать штриховыми линиями. Опре­деляется натуральная величина треу­гольника DEK.

Плоскопараллельным перемещени­ем треугольник приводится в по­ложение проецирующей плоскости и далее вращением вокруг проецирующей прямой в положение, когда он будет параллелен плоскости проек­ций. В треугольнике DEK следует показать и линию MN пересечения его с плоскостью α.

Выполнив все построения в каран­даше, чертеж обводят цветной пастой. Вначале, черной пастой обводят линии задан­ных треугольников, а красной пас­той — линию пересечения треугольни­ков. Все вспомогательные построения должны быть обязательно показаны на чертеже в виде тонких линий карандашом.

Видимые части треугольников в проекциях можно отмыть или покрыть очень блед­ными тонами цветных карандашей. Все буквенные или циф­ровые обозначения, а также надписи обводят черной пастой.

Таблица 1. Данные к задаче 1 (размеры и координаты, мм)

№ вар	A			B			C			D			E			F
	X	y	Z	x	y	z	x	y	Z	X	y	Z	x	y	z	x	y	z
1	120	90	10	30	25	20	0	85	50	70	110	85	135	20	35	15	50	0
2	142	23	52	22	53	97	62	108	22	137	53	17	82	112	97	22	23	47
3	140	20	50	25	60	20	65	105	15	130	60	10	85	110	85	19	25	35
4	152	3	62	32	42	108	72	98	32	147	42	27	92	103	108	32	12	58
5	143	15	43	30	55	85	70	100	10	135	55	15	90	105	90	15	20	40
6	130	30	40	15	70	70	55	115	5	120	70	0	75	120	75	0	35	25
7	137	18	47	17	58	92	57	113	17	132	58	12	77	118	92	17	28	42
8	117	9	70	90	100	10	0	20	58	68	110	85	135	19	16	14	52	0
9	120	90	10	50	20	75	0	20	40	70	115	85	135	20	32	10	50	0
10	133	25	45	20	65	75	60	110	101	125	65	5	80	115	80	5	30	30
11	147	8	57	27	48	102	67	103	27	142	48	22	87	198	102	27	18	52
12	155	5	65	40	45	95	80	90	30	145	45	25	100	95	100	25	10	50
13	127	28	37	7	68	82	47	123	7	122	68	3	67	128	82	7	38	32
14	115	7	85	50	80	25	0	50	80	75	85	110	100	55	35	15	0	50
15	150	10	65	35	50	90	75	95	25	140	50	20	95	100	95	20	15	45
16	132	23	42	12	63	87	52	118	12	127	63	8	72	118	87	12	33	37
17	117	9	90	52	79	25	0	48	83	68	85	110	135	30	49	74	0	35
18	115	90	10	52	25	90	0	80	45	65	105	80	130	18	35	12	50	0
19	120	82	15	48	15	85	10	10	35	60	115	90	140	15	40	8	54	5
20	108	95	0	54	30	90	15	75	40	65	110	95	130	20	45	12	60	10

Лист 2

Задача 2. Построить проекции пира­миды, основанием которой является четырехугольник ABCD, а ребро SA опре­деляет высоту h пирамиды. Данные для своего варианта взять из табл. 2.

Указания к решению задачи 2. В левой половине листа формата A3 намечаются оси координат и из табл. 2 согласно своему варианту берутся координаты точек А, В, C и D вершин четырехугольника ABCD. По координатам строится четырехугольник в проекциях. В точке А восставляется перпен­дикуляр к плоскости треугольника, находится его натуральная величина и на ней выше этой плоскости откла­дывается отрезок AS, равный задан­ной величине h. Строятся ребра пи­рамиды. Ви­димые ребра пирамиды следует пока­зать сплошными основными линиями, невидимые — штриховыми линиями. Стороны четырехугольника ABCD (основа­ние пирамиды) следует обвести черной пастой; ребра SA, SB, и SC и SD пирамиды обвести красной пастой. Все вспомо­гательные построения необходимо сох­ранить на эпюре и показать их тонки­ми сплошными линиями карандашом.

Таблица 2. Данные к задаче 2 (координаты и размеры, мм)

№ Вар.	Точка А			Точка В			Точка С			Точка D		h
	X	y	Z	x	Y	Z	X	y	z	x	z
1	150	48	50	95	75	80	40	62	73	62	44	80
2	130	50	52	75	78	80	20	64	76	40	44	80
3	40	62	76	95	75	80	150	48	50	40	44	80
4	30	64	76	70	78	82	130	50	52	50	50	80
5	135	22	68	95	8	44	45	62	94	70	80	75
6	45	70	74	95	10	60	135	40	74	70	80	75
7	45	60	82	95	12	25	135	35	55	75	95	75
8	45	80	75	90	38	10	135	35	55	75	90	75
9	45	70	90	110	15	8	130	30	70	72	100	80
10	54	70	50	100	20	0	125	30	30	90	60	80
11	55	60	40	100	20	0	125	30	30	90	60	80
12	125	30	30	100	25	0	55	60	40	90	60	80
13	96	30	65	70	95	25	25	70	73	60	85	80
14	92	50	35	15	50	10	40	30	60	58	80	85
15	60	15	80	90	120	35	15	10	100	40	60	90
16	100	90	60	22	120	82	40	50	30	60	0	85
17	80	95	52	0	110	85	28	20	20	50	15	80
18	75	95	0	105	60	40	115	135	70	80	35	80
19	75	30	0	150	120	22	110	15	90	70	35	75
20	70	15	50	125	55	10	45	45	5	15	25	75

Задача 3. Построить линию пере­сечения пирамиды с прямой призмой, усеченной фронтально-проецирующей плоскостью α, проходящей через вершину ребра призмы Е высотой 85 мм параллельно фронтальной проекции ребра пирамиды DB( D₂B₂). Данные для своего варианта взять из табл. 3. Пример выполнения листа 2 приведен на рис. 2.

Указания к решению задачи 3. В оставшейся правой половине листа 2 намечаются оси координат и из табл. 3 согласно своему варианту берутся координаты точек А, В, С и D вершин пирамиды и координаты точек Е, F, G и U вершин многоугольника нижнего основания призмы, а также высота h призмы. По этим данным строятся проекции многогранников (пирамида и призма).

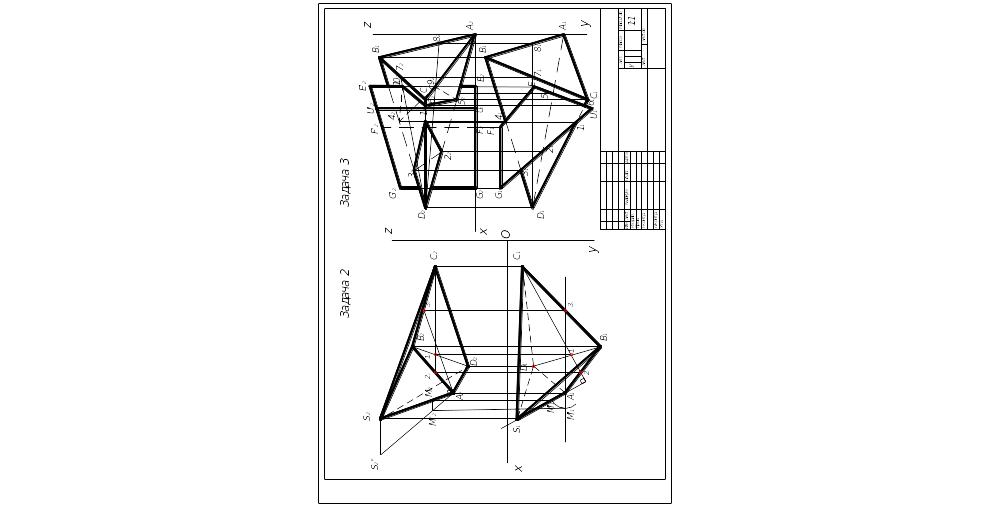
Призма своим основанием стоит на плоскости уровня, горизон­тальные проекции ее вертикальных ребер преобразуются в точки. Грани боковой поверхности призмы пред­ставляют собой отсеки горизонтально проецирующих плоскостей.

Линии пересечения многогранников определяются по точкам пересечения ребер каждого из них с гранями дру­гого многогранника или построением линии пересечения граней многогран­ника. Соединяя каждые пары таких точек одних и тех же граней отрезками прямых, получаем линию пересечения многогранников.

Видимыми являются только те сто­роны многоугольника пересечения, ко­торые принадлежат видимым граням многогранников. Их следует показать сплошными жирными линиями крас­ной пастой, невидимые отрезки прост­ранственной ломаной показать штри­ховыми линиями красной пастой. Все вспомогательные построения на эпюре сохранить и показать их тонкими карандашными линиями.

Примечание. Задаче 3 уделить особое внимание. Все построения на чертеже тщательно проверить. Допу­щенные ошибки приводят к неправиль­ному решению следующей задачи — задачи 4 (построение развертки мно­гогранников).

Таблица 3. Данные к задаче 3 (координаты и размеры, мм)

№ Вар	A			B			C			D			E		F		G		U		hE
	X	y	z	x	y	z	x	y	Z	X	y	z	x	y	x	y	X	y	x	y
1	150	98	0	125	10	82	90	130	40	0	75	40	102	52	76	22	12	22	55	88	85
2	150	90	0	120	5	80	85	130	42	0	80	42	102	54	74	18	15	18	58	86	85
3	146	95	0	120	24	77	87	125	40	0	78	40	100	50	74	20	16	20	55	90	85
4	140	75	0	126	15	75	90	105	42	0	50	42	100	50	74	20	16	20	55	90	85
5	140	72	0	116	15	80	80	102	40	0	52	40	100	50	74	20	16	22	55	85	85
6	142	92	0	125	20	80	85	125	40	0	65	40	100	50	74	20	16	20	55	85	85
7	140	75	0	122	14	77	87	100	40	0	50	40	100	50	75	20	15	20	55	90	85
8	0	70	0	24	10	75	52	96	40	142	45	40	40	50	67	20	125	20	86	90	85
9	0	80	0	20	18	76	53	100	40	142	55	40	40	50	67	20	125	20	85	90	85
10	0	80	0	20	18	76	53	110	40	140	55	40	40	50	66	20	125	20	86	90	85
11	0	68	0	20	8	76	55	92	40	140	45	40	40	50	66	20	124	20	85	90	85
12	0	75	0	20	14	76	55	110	40	142	50	40	40	50	67	22	125	22	85	90	85
13	145	80	0	122	20	75	88	110	40	0	55	40	100	50	74	22	16	22	55	90	85
14	145	68	0	122	8	78	88	100	40	0	45	40	100	50	74	22	16	22	55	88	85
15	142	82	0	120	20	78	88	112	40	0	57	40	100	50	74	20	15	20	55	88	85
16	0	82	0	20	20	78	54	114	40	140	57	40	40	50	67	20	125	20	86	90	85
17	0	85	0	20	25	78	55	115	40	140	60	40	40	50	68	22	125	22	86	90	85
18	0	90	0	20	30	78	55	120	40	140	65	40	40	50	68	22	125	22	86	90	85
19	0	85	0	15	30	80	55	125	40	140	60	40	40	50	68	22	125	22	86	90	85
20	142	70	0	122	10	78	88	95	40	0	45	40	100	50	75	22	16	22	55	90	85

Лист 3

Задача 4. Построить развертки пе­ресекающихся многогранников — прямой призмы с пирамидой. Пока­зать на развертках линию их пересе­чения. Пример выполнения листа 3 приведен на рис. 3.

Чтобы решить данную задачу, чертеж-задание для листа 3 получить, переведя на кальку формата 297х Х420 мм чертеж пересекающихся многогранников с листа 2 (задача 3).

Указания к решению задачи 4. За­данные элементы многогранников на кальке показать черной пастой: линии их пересечения обвести красной пас­той. Здесь выполняются вспомогатель­ные построения (их обвести синей или зеленой пастой) для определения на­туральных величин ребер многогран­ников.

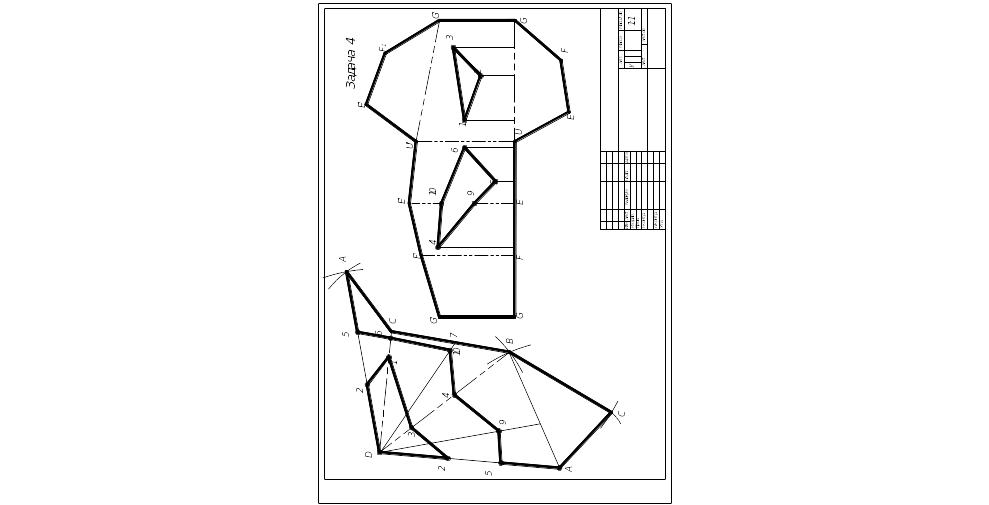
На листе бумаги ватман формата A3 (297x420 мм) строятся развертки многогранников.

Развертка прямой призмы. Для построения развертки прямой призмы поступают следующим обра­зом:

а) проводят горизонтальную пря­мую.

б) от произвольной точки G этой прямой откладывают отрезки GU, UЕ, EF, FG, равные длинам сторон основания призмы;

в) из точек G, U,.... ' восставляют перпендикуляры и на них откладывают величины, равные высоте призмы. По­лученные точки соединяют прямой. Прямоугольник FF₁F₁F является раз­верткой боковой поверхности призмы. Для указания на развертке граней призмы из точек U, Е, G восставляют перпендикуляры;

г) для получения полной развертки поверхности призмы к развертке по­верхности пристраивают многоуголь­ники ее оснований.

Для построения на развертке линии пересечения призмы с пирамидой замкнутых ломаных линий 1 2 3 и 45678 пользуемся вертикальными прямыми. Например, для определения положения точки 1 на развертке пос­тупаем так: на отрезке GU от точки G вправо откладываем отрезок G1₀, равный отрезку G1 (рис. 3).

Из точки 1₀ восставляем перпенди­куляр к отрезку GU и на нем откла­дываем – высоту (значение z) откладываем от основания призмы(точки 1). Анало­гично строят и находят остальные точки.

Развертка пирамиды. На кальке определяют натуральную вели­чину каждого из ребер пирамиды. Зная натуральные величины ребер пирамиды, строят ее развертку. Опре­деляют последовательно натуральные величины граней пирамиды. На ребрах и на гранях пирамиды (на развертке) определяют вершины пространствен­ной ломаной пересечения пирамиды с призмой.

Развертки многогранников отмыть цветной акварелью, чаем или покрыть цветным карандашом. Ребра многогранника на развертке обвести черной пастой; линии пересечения многогранников обвести красной, а все вспомогательные построения — карандащом. Кальку приложить к альбому чертежей.

Лист 4

Задача 5. На трехпроекционном чер­теже построить недостающие точки сквозного отверстия в сфере заданного радиуса R. Фронтальная проекция сквозного отверстия представлена частью цилиндрического отверстия радиуса R₁ с центром в точке О (центр сферы) и точками А, В и С – проекциями ребер призматического отверстия. Точка С лежит на окружности радиуса R₁ - проекции цилиндрического отверстия (табл. 5).

Указания к решению задачи 5. В центре формата А3 намечают оси координат. Строят проекции сферы заданного радиуса R с центром в точке О. Проводят окружность R₁ из т. О₂. На­мечаются оси координат с началом координат в центре незаполненной части листа формата A3. Строятся проекции сферы заданного радиуса R с центром в точке О. Определяют по заданным координатам (табл. 5) проекции точек А, B и С - вершин сквозного отверс­тия на

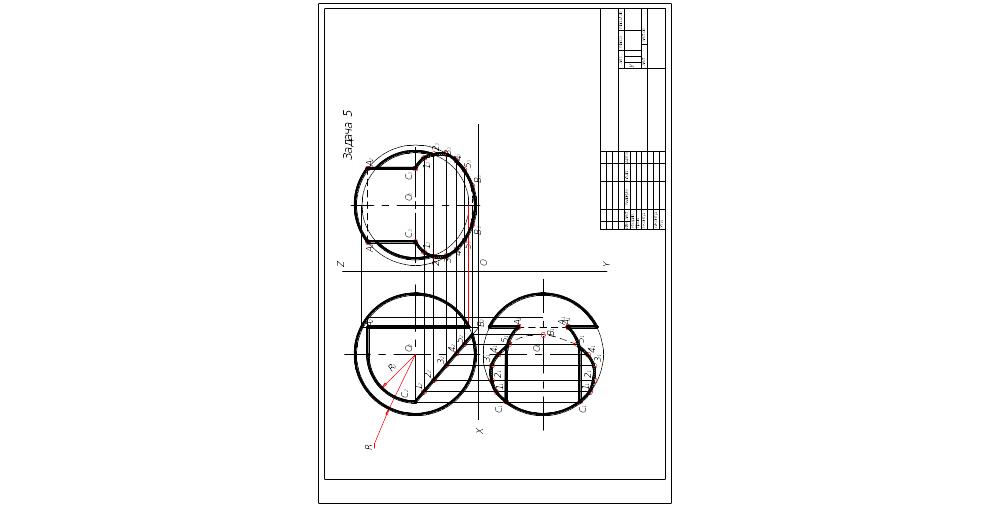
сфере и строится многоуголь­ник — вырожденная проекция линии сквозного отверстия. Далее задача сводится к определению недостающих проекций точек поверхности сферы. Вначале определяются характерные точки линии сквозного отверстия: точки на экваторе, главном меридиане, наиболее удаленные и ближайшие точки поверхности сферы к плоскостям проекций. Очертание сферы и вырож­денную проекцию сквозного сечения обвести черной пастой, недостающие две проекции отверстия показать крас­ной пастой. Все вспомогательные пост­роения на чертеже сохранить и обвести тонкими линиями карандашом. В целях наибольшей наглядности чертежа сферу в проекциях можно отмыть бледными тонами акварели или цветного карандаша.

Таблица 5. Данные к задаче 5

№ вар	О			А		В		C	R	R1
	X	y	z	x	z	X	y	x
1	70	60	60	50	100	50	0	110	52	40
2	70	70	60	48	100	48	2	100	52	40
3	75	70	60	53	98	53	0	110	55	38
4	75	60	70	53	110	53	6	110	58	40
5	70	75	75	50	115	50	10	110	55	40
6	80	70	75	110	115	110	15	40	52	40
7	80	75	80	115	120	115	20	40	50	40
8	80	72	70	108	110	108	10	35	50	40
9	80	75	72	112	112	112	12	35	55	40
10	80	75	60	112	102	112	0	38	52	42
11	80	60	75	115	33	115	135	38	55	42
12	75	70	70	110	28	110	130	33	58	42
13	75	75	75	110	33	110	130	33	60	42
14	80	60	70	115	30	115	125	40	56	40
15	80	70	75	115	38	115	130	43	60	37
16	80	80	70	55	33	55	130	117	60	37
17	70	75	75	45	37	45	135	108	60	38
18	70	80	80	48	42	48	140	103	58	38
19	80	60	80	52	40	52	135	120	60	40
20	80	80	75	52	37	52	135	110	60	38

Лист 5

Задача 6. Построить линию пере­сечения конуса вращения плоскостью ABC общего положения. Данные для своего варианта взять из табл. 6. Пример выполнения листа 5 приведен на рис. 5.

Указания к решению задачи 6. В левой половине листа формата A3 намечаются оси координат и из табл. 6 согласно своему варианту берутся величины, которыми задаются поверх­ность конуса вращения и плоскость ABC. Определяется центр (точка К) окружности радиусом R основания конуса вращения в плоскости уровня. На вертикальной оси, на расстоянии h от плоскости уровня и выше ее, опре­деляется вершина конуса вращения. По координатам точек А, В, С опре­деляется секущая плоскость.

В целях облегчения построения ли­нии сечения строится дополнительный чертеж заданных геометрических об­разов. Выбирается дополнительная система П₃П₄) плоскостей проекций с таким расчетом, чтобы секущая плос­кость была представлена как проеци­рующая. Дополнительная плоскость проекций П₃ перпендикулярна данной плоскости ABC. Линия сечения (эл­липс) проецируется на плоскость проекций П₃ в виде отрезка прямой на следе этой плоскости. Имея проек­цию эллипса сечения на дополнитель­ной плоскости П₃, строят основные ее проекции.

Оси координат, очертания поверх­ности на основном эпюре и секущую плоскость следует обвести черной пас­той; линий сечения в проекциях обвес­ти красной пастой. Все основные и вспомогательные построения на основ­ном и дополнительных эпюрах сохра­нить и показать тонкими сплошными линиями карандашом.

Таблица Данные к задаче 6 (координаты и размеры, мм)

№ вар.	К			A			B			C			R	h
	x	y	z	x	y	z	x	y	z	x	y	z
1	78	65	0	12	40	70	45	40	70	90	140	8	46	100
2	80	65	0	50	28	66	12	42	66	90	140	4	46	100
3	80	66	0	50	30	64	12	46	64	85	128	4	43	102
4	80	66	0	44	32	60	15	50	60	85	132	5	43	102
5	78	72	0	10	50	62	46	30	62	82	125	10	45	100
6	78	72	0	82	25	62	10	50	62	46	130	8	45	100
7	80	66	0	44	30	60	15	50	60	86	132	5	42	102
8	82	65	0	45	30	62	15	48	62	86	130	5	42	102
9	80	72	0	46	30	62	82	115	10	10	120	8	45	100
10	80	70	0	10	50	62	82	25	10	46	130	8	45	100
11	82	65	0	45	32	62	15	48	62	84	135	0	43	100
12	84	65	0	45	28	66	10	50	66	84	135	0	43	100
13	78	70	0	46	30	62	10	50	62	82	125	10	44	102
14	80	72	0	45	30	60	10	50	60	80	125	8	45	98
15	84	64	0	45	30	66	10	52	66	85	136	5	44	100
16	86	64	0	44	30	65	14	52	65	88	136	4	44	100
17	80	68	0	46	28	60	10	48	60	80	126	0	45	98
18	82	68	0	47	28	65	10	50	65	82	126	6	45	98
19	82	68	0	49	30	66	12	48	66	84	130	5	44	102
20	82	68	0	48	28	65	10	52	65	84	128	6	43	98

Задача 7. Построить линию пересе­чения конуса вращения с призмой, основанием которой является треугольник АВС. Определить натуральную величину фигуры сечения конуса с гранью призмы АВ. Данные для своего варианта взять из табл. 7.

Указания к решению задачи 7. В правой половине листа намечают оси координат и из табл. берут согласно своему варианту величины, которыми задаются поверхности конуса враще­ния и призмы. Грани призмы являются фронтально проецирующими плоскостями, треугольники оснований АВС – горизонтально проецирующими.

Опорные точки находим как точки пересечения очерковых образующих конуса с плоскостями призмы. Промежуточные точки находятся с помощью вспомогательных плоскостей горизонтального уровня.

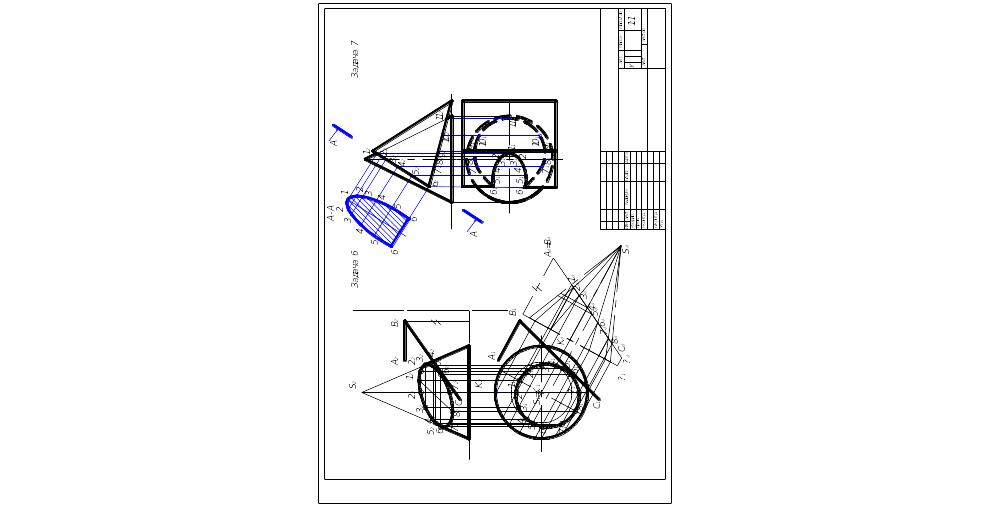
Натуральную величину фигуры сечения выполнить на дополнительной плоскости параллельной грани призмы АВ (метод замены плоскостей проекций)

Таблица Данные к задаче 7 (координаты и размеры, мм)

№ вар	К			R	h	A		B		C		l
	x	y	z			X	z	x	z	x	z
1	70	70	0	46	102	92	40	55	68	30	10	104
2	70	65	0	44	105	100	20	50	50	46	3	120
3	75	70	0	50	102	98	20	48	52	30	10	102
4	75	72	0	44	98	90	30	48	48	25	8	100
5	72	10	0	45	106	106	10	55	75	28	5	104
6	70	75	0	46	102	112	24	50	70	32	10	106
7	80	70	0	45	106	126	26	60	80	35	5	100
8	80	72	0	48	103	130	30	50	65	35	5	108
9	80	75	0	50	100	115	34	34	96	30	8	110
10	80	76	0	50	102	38	30	103	70	134	11	112
11	78	74	0	48	102	62	50	100	80	130	10	110
12	78	75	0	50	102	60	65	100	95	130	10	110
13	70	74	0	48	104	30	35	110	60	120	0	106
14	80	75	0	46	102	58	64	135	28	98	2	108
15	80	70	0	50	102	60	80	110	30	25	5	112
16	70	72	0	44	106	64	85	112	35	24	8	100
17	70	72	0	48	102	60	88	108	38	40	48	108
18	80	68	0	50	104	25	8	66	85	115	45	110
19	78	74	0	43	100	72	96	112	26	40	56	100
20	75	70	0	46	102	80	0	40	65	80	65	104

Лист 6

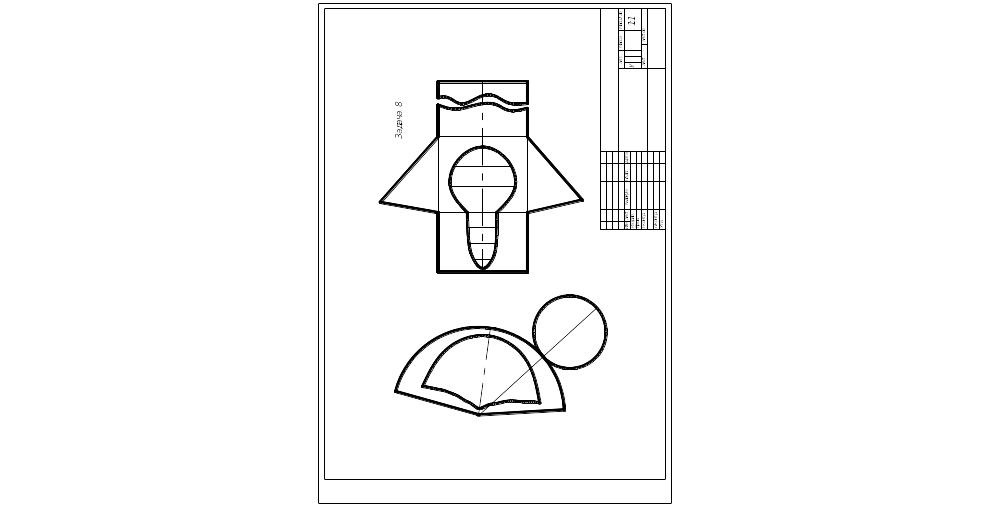
Задача 8. Построить развертки пересекающихся конуса вращения и прямой трехгранной призмы с основанием АВС. Показать на развертках линии их пересечения. Чертеж-задание для задачи 9 получить, переведя на кальку формата A3 (297X420 мм) чертеж пересекающих­ся поверхностей с листа задачи 8 (рис. 5). Пример выполнения листа 6 приведен на рис. 6.

Указания к решению задачи 8.

Развертка конуса враще­ния. Разверткой поверхности конуса вращения является круговой сектор с углом α = R/( Lx360), где R — ра­диус окружности основания конуса вращения; L — длина образующей.

На развертке конуса вращения строят прямолинейные образующие или параллели, проходящие через ха­рактерные точки линий пересечения конуса вращения с призмой. Построить круг основания конуса.

Развертка призмы. Для построения развертки прямой призмы поступают следующим образом: а) строят горизонтальный прямоугольник с длиной равной длине призмы l. б) проводят среднюю горизонтальную линию; в) отмечают по длинной стороне положение ребер призмы АВС и расстояния до точек пересечения, взятые с чертежа. Задачи 8 по периметру сторон; г) Из полученных точек восстанавливают перпендикуляры, на которых от средней линии откладывают расстояние между точками пересечения, взятых по длине призмы. Достроить треугольники основания призмы.

Задача 9. Построить линию пересе­чения закрытого тора с поверхностью наклонного конуса вращения. За­данные поверхности имеют общую фронтальную плоскость симметрии. Найти точки встречи горизонтальной прямой АВС поверхностью тора. Данные для своего варианта взять из табл. 10. Пример выполнения лис­та приведен на рис. 8.

Таблица 10. Данные к задаче 9 (координаты и размеры, мм)

№ Вар.	К			E			Rт	Α	Rк	А			Β
	x	y	z	x	y	z				x	y	z	x	y	z
1	70	70	0	70	70	34	55	55	46	140	50	28	30	145	25
2	70	70	0	70	70	34	55	55	46	135	50	25	30	145	25
3	70	70	0	70	70	36	55	55	50	135	45	28	30	140	25
4	65	70	0	65	72	36	53	55	46	130	40	28	30	140	28
5	65	72	0	65	72	36	53	55	46	130	40	28	30	135	28
6	66	72	0	66	72	35	52	60	44	130	40	28	25	135	28
7	68	74	0	68	74	35	53	60	44	130	40	30	25	135	30
8	68	74	0	68	74	35	54	45	48	135	40	30	25	135	30
9	70	75	0	70	75	36	52	45	44	140	40	30	25	135	30
10	70	72	0	70	72	36	52	45	44	140	45	30	20	140	30
11	70	70	0	70	70	40	50	60	40	130	45	25	30	130	25
12	68	74	0	68	74	34	55	50	50	135	40	35	20	140	30
13	72	75	0	72	75	35	54	60	45	140	40	35	20	145	32
14	70	70	0	70	70	38	52	55	46	130	45	90	30	130	30
15	65	72	0	65	72	35	54	55	48	140	50	30	20	140	30
16	65	72	0	65	72	35	54	55	48	140	50	30	20	140	30
17	66	72	0	66	72	35	55	50	50	140	50	35	20	140	30
18	70	72	0	70	72	36	52	45	44	140	45	30	20	140	30
19	66	72	0	66	72	35	55	50	50	140	50	35	20	140	30
20	70	70	0	70	70	40	52	60	40	130	45	25	30	130	25

Указания к решению задачи 9. В левой половине листа формата A3 намечают оси координат и из табл. согласно своему варианту берут за­данные величины, которыми определя­ются поверхности тора и цилиндра вращения. Определяют по координа­там положение точки Е, т. е. точки пересечения вертикальной оси тора с наклонной осью цилиндра вращения радиуса г = 2 R/3

Главным меридианом поверхности тора является замкнутая линия, состоящая из двух пересекающихся на оси вращения дуг окружностей радиуса 2R и отрезка прямой — проекции экваториальной параллели, представляющей собой окружность с центром в точке К и радиусом R в плоскости уровня хОу.

Ось цилиндра вращения пересека­ется с осью поверхности тора в точке Е под углом δ. Основание цилиндра вращения касается профильной коор­динатной плоскости уОz.

Точки пересечения фронтальных меридианов заданных поверхностей вращения принадлежат искомой ли­нии их пересечения. Они определяются на чертеже без каких-либо дополни­тельных построений. Другие точки линии пересечения можно построить, используя (как вспомогательные секу­щие) концентрические сферические посредники.

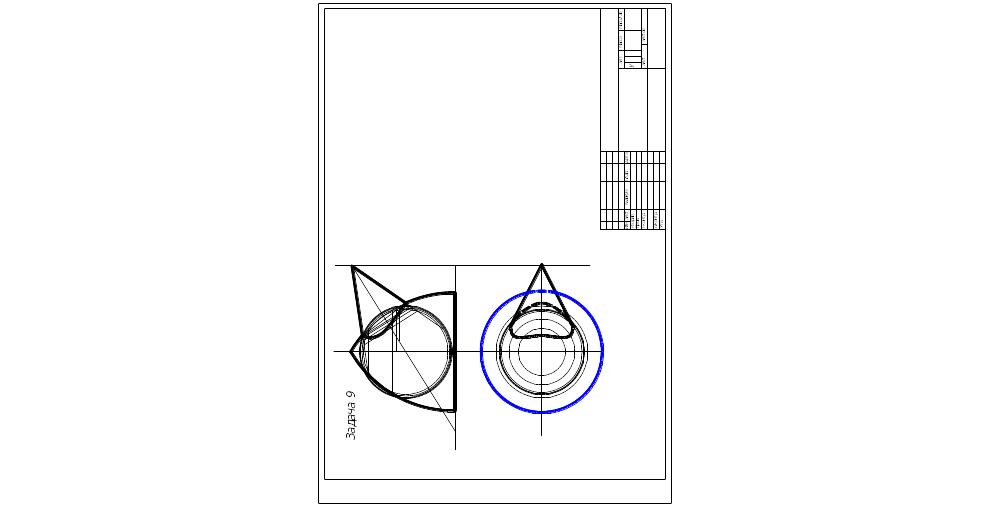
Из точки пересечения осей как из центра проводится сфера произволь­ного радиуса. Она пересекает обе поверхности по окружностям. Фрон­тальные поверхности окружностей изображаются отрезками прямых ли­ний, которые пересекаются в точках, являющихся фронтальными проекция­ми точек искомой линии пересечения поверхностей. Изменяя радиус вспо­могательной секущей сферы, можно получить последовательный ряд точек линии пересечения.

Определив достаточное число точек для построения линии пересечения поверхностей и определив ее види­мость в проекциях, чертеж обводят пастой. Оси координат и линии, задаю­щие поверхности, следует обвести чер­ной пастой; линию пересечения по­верхностей выделить красным цветом, а все основные вспомогательные построения обвести карандашом.