
- •50 Часов — лекционных занятий;
- •25 Часов — практических занятий;
- •25 Часов — лабораторных занятий. Содержание
- •Лекция 1. Общие вопросы теории моделирования (2 часа) План
- •2. Роль и место моделирования в исследованиях систем
- •3. Классификация моделей
- •4. Моделирование в процессах познания и управления
- •5. Классификация объектов моделирования
- •6. Основные этапы моделирования
- •7. Этапы моделирования объектов (процессов, явлений)
- •Контрольные вопросы
- •Литература
- •Лекция 2. Технология моделирования (2 часа) План
- •2. Подготовка исходных данных
- •3. Разработка математической модели
- •4. Выбор метода моделирования
- •2. Проверка адекватности и корректировка модели
- •3. Планирование экспериментов с моделью
- •4. Анализ результатов моделирования
- •2. Сведения об объекте
- •3. Априорная информация
- •4. Апостериорная информация
- •1. Постановка задачи идентификации.
- •2. Трудности идентификации
- •1. Постановка задачи идентификации.
- •Следовательно модельный оператор f должен быть таким, чтобы:
- •2. Трудности идентификации
- •1. Идентификация структуры и параметров объекта
- •2. Классификация методов идентификации
- •1. Идентификация структуры и параметров объекта
- •2. Классификация методов идентификации
- •2. Ранжирование входов и выходов объекта (Метод экспертных оценок)
- •Метод непосредственного ранжирования;
- •Метод парных сравнений.
- •3. Метод непосредственного ранжирования
- •2. Определение рационального числа входов и выходов объекта, учитываемых в модели
- •3. Определение характера связи между входом и выходом модели объекта
- •1. Потоки заявок
- •2. Марковские модели
- •1. Потоки заявок
- •2. Марковские модели
- •2. Характеристики вычислительных систем как сложных систем массового обслуживания
- •3. Методы приближённой оценки характеристик вычислительных систем
- •1. Нестационарные режимы функционирования вычислительных систем
- •2. Характеристики вычислительных систем как стохастических сетей
- •1. Нестационарные режимы функционирования вычислительных систем
- •2. Характеристики вычислительных систем как стохастических сетей
- •2. Обобщенные алгоритмы имитационного моделирования
- •2. Метод повторных экспериментов
- •3. Методы генерации случайных величин и последовательностей
- •Контрольные вопросы
- •II. Модель в - для задачи максимизации
- •2. Преобразование задачи с дискретными переменными к задаче с булевыми переменными
- •3. Преобразование задачи линейного булева программирования к задаче нелинейного булева программирования
- •Контрольные вопросы
- •2. Модель задачи автоматической классификации
- •3. Задача об оптимизации размещения букв алфавита на клавиатуре эвм
- •2. Проверка адекватности математической модели
- •3. Алгоритм оптимального управления работы насосной станции
- •Контрольные вопросы
- •2. Аналитический подход к формированию информативной подсистемы признаков в задаче распознавания
- •3. Упрощенный метод классификации с использованием аналитического подхода формирования информативной подсистемы признаков при наличии обучающей выборки
- •Контрольные вопросы
- •Литература
- •Литература
Контрольные вопросы
Роль и место моделей булева программирования в проблеме оптимизации.
Основные виды моделей линиейного булева программирования.
О полиномиальных и не полиномиальных задачах в дискретной оптимизации.
Преобразование задачи с дискретными переменными к задаче с булевыми переменными.
Преобразование задачи *** к задаче нелинейного булева программирования.
Как записывается функционал Фишерского типа.
Литература
Лекция 15. НОВЫЕ МОДЕЛИ ЗАДАЧ ЛИНЕЙНОГО БУЛЕВА ПРОГРАММИРОВАНИЯ (2 часа)
План
1. Задача и модель оптимизации работы насосной станции
2. Модель задачи автоматической классификации
3. Задача об оптимизации размещения букв алфавита на клавиатуре ЭВМ
1. Задача и модель оптимизации работы насосной станции
Исследование и моделирование крупных насосных станций является одной из ключевых задач в системе машинного водоподъема (СМВ). В настоящее время в СМВ в основном используется диспетчерское управление, основанное на простых методах принятия решений, исходя из личного опыта и интуиции лица, принимающего решения (диспетчера) и решающего задачу управления для текущего момента времени. Такое управление приводит к перерасходу электроэнергии на водоподъем, непроизводительным сбросам и потерям воды, невыполнения графика водоподачи. Поэтому задачи, связанные с исследованием, моделированием и разработкой оптимальных алгоритмов управления работой насосной станции, особенно становятся актуальными в связи с переходом к рыночным условиям хозяйствования.
Исследуем работу насосной станции и определим ее основные управляющие параметры.
В крупных насосных станциях обычно устанавливается несколько насосных агрегатов, предназначенных для подъема воды на высоту определенного диапазона. В большинстве случаев насосная станция работает в режимах, при которых недоиспользуются полные возможности, заложенные в насосных агрегатах. Следовательно, возникает необходимость создания таких методов управления, которые позволяют максимально использовать все потенциальные возможности насосной станции и создать оптимальную систему управления по заданному критерию.
В насосных станциях
используются крупные осевые насосные
агрегаты типа "Р" и "ОП",
центробежные типа "В". Для подъема
воды на высоту до 25 м используются осевые
насосные агрегаты, а на высоту более 25
м -центробежные. Для моделирования
процесса водоподачи основными являются
гидроэнергетические и расходные
характеристики. Гидроэнергетические
характеристики можно найти в каталогах.
Расходная характеристика Q насосного
агрегата зависит от высоты подъема H
и от угла
![]() разворота лопасти насосного агрегата:
разворота лопасти насосного агрегата:
![]() .
.
В каталогах насосных агрегатов расходная характеристика осевого насосного агрегата задается в виде семейства кривых при различных углах разворота лопастей:
![]() ,
(j=1,2,...,n),
,
(j=1,2,...,n),
где
![]() - угол разворота лопастей, соответствующий
j-ой кривой; n - количество кривых.
- угол разворота лопастей, соответствующий
j-ой кривой; n - количество кривых.
Таким образом, расходная характеристика насосного агрегата полностью определяется двойкой
![]()
Состояние насосной станции определяется количеством работающих насосных агрегатов mp из общего числа насосных агрегатов m и последовательностью углов разворота лопастей работающих насосных агрегатов
![]()
Например, i-й насосный агрегат может работать в n положениях
![]() (i=1,2,...,m),
(i=1,2,...,m),
т.е. положение насосного агрегата определяется положением угла разворота лопастей.
Для работающих насосных агрегатов насосной системы введем следующие обозначения:
![]() ,
,
![]() ,
,
где MP - множество номеров работающих насосных агрегатов;
![]() -
множество углов разворота лопастей
работающих насосных агрегатов.
-
множество углов разворота лопастей
работающих насосных агрегатов.
Следовательно,
состояние насосной станции в каждый
момент времени определяется тройкой
![]() .
.
Общая расходная характеристика насосной станции, соответствующая ее состоянию, определяется как алгебраическая сумма расходов каждого работающего насосного агрегата:
![]() ,
,
где Qi(H,i) - расходная характеристика i-го насосного агрегата;
H - высота подъема воды;
i - угол разворота лопастей i-го насосного агрегата.
Потребляемая мощность насосной станции также определяется как алгебраическая сумма мощностей каждого работающего насосного агрегата:
![]() ,
,
где
![]() /кВт/ - мощность i-го насосного
агрегата;
/кВт/ - мощность i-го насосного
агрегата;
Hi -напор, м;
Qi -расход i-го насосного агрегата, м3 /с;
![]() -КПД i-го насосного агрегата.
-КПД i-го насосного агрегата.
Оптимизация управления заключается в определении количества и номеров работающих насосных агрегатов, а также углов разворота их лопастей, обеспечивающих минимум потребляемой насосной станцией мощности для реализации заданного графика водоподачи.
Приводим постановку задачи оптимизации, которая является общепринятой в СМВ.
Пусть управляемый процесс в области
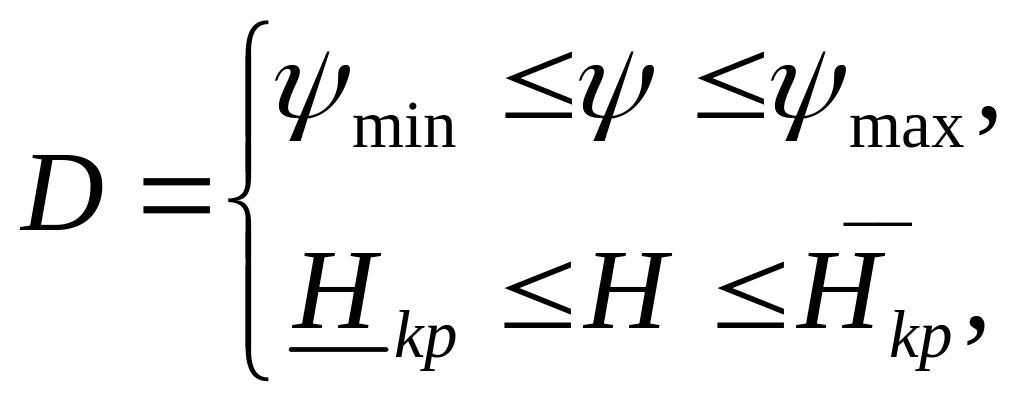
характеризуется определением регулирующей тройки
, (1)
где min и max - минимальное и максимальное допустимые значения углов разворота лопастей насосных агрегатов;
![]() и
и
![]() - критические значения уровней верхнего
и нижнего бьефов насосных станций, при
которых требуется минимизировать
функционал
- критические значения уровней верхнего
и нижнего бьефов насосных станций, при
которых требуется минимизировать
функционал
![]() (2)
(2)
с выполнением ограничения следующего вида
![]() , (3)
, (3)
здесь =0.05*Qn - допустимая погрешность управления.
Задача оптимизации (2), (3) с оптимизируемой тройкой параметров (1) не подлежит эффективному решению существующими методами. В связи с этим возникшую задачу сформулируем как задачу линейного булева программирования в обобщенной постановке.
Предполагается, что в насосной станции имеются m насосных агрегатов:
P1, P2, ... , Pm .
Насосный агрегат Pi может работать в ni положениях
![]() (4)
(4)
где ni -количество углов разворота лопастей i-го насосного агрегата; причем рассматривается случай, когда количество углов разворота лопастей для разных насосных агрегатов различно; кроме того, насосный агрегат Pi может находиться только в одном из перечисленных положений (4).
Известна производительность (производительность насосных агрегатов обычно регулируется углом разворота лопастей рабочего колеса работающих насосных агрегатов) каждого положения i-го насосного агрегата, т.е.
![]()
где qij - расходная характеристика i-го насосного агрегата при j-м положении угла разворота лопастей.
Также считаются известными значения следующих параметров
![]() ,
,
где cij - потребляемая мощность i-го насосного агрегата при j-м положении угла разворота лопастей.
Введем булевые переменные xij по следующему правилу: xij=1, если i-й насосный агрегат работает в j-м положении; xij=0 -в противном случае.
Задача оптимизации работы насосной станции может быть сформулирована как задача линейного булева программирования следующего вида:
 (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
где
![]() и
и
![]() нижний и верхний пределы общей расходной
характеристики насосной станции.
нижний и верхний пределы общей расходной
характеристики насосной станции.
По полученному решению задачи (5)-(7) можно устанавливать количество и номера работающих насосных агрегатов. Количество работающих насосных агрегатов определяется из соотношения
![]()
где
![]() -(i=1,2,...,m;
j=1,2,...,ni) - решение задачи
(5)-(7). Номера работающих насосных
агрегатов определяются из следующего
условия: если для произвольного значения
i
=1
(j=1,2,...,ni), то i-й
насосный агрегат работает.
-(i=1,2,...,m;
j=1,2,...,ni) - решение задачи
(5)-(7). Номера работающих насосных
агрегатов определяются из следующего
условия: если для произвольного значения
i
=1
(j=1,2,...,ni), то i-й
насосный агрегат работает.
Здесь путем минимизации целевой функции (5) уменьшается общая потребляемая мощность насосной станции. Выполнения ограничения вида (6) обеспечивает подъем воды в допустимых пределах [ , ]. Выполнением ограничения вида (7) обеспечивается работа каждого насосного агрегата только в одном из возможных положений (4).
