2. Характеристики вычислительных систем как сложных систем массового обслуживания

Многомерный поток. На вход обслуживающего прибора может поступать многомерный поток заявок, состоящий из заявок типов 1, ..., М, у которых интенсивности равны Предположим, что каждый из потоков заявок одного типа является простейшим. Загрузка прибора потоком заявок типа i будет составлять

где — средняя длительность обслуживания заявок типа i. Суммарная загрузка прибора со стороны всех потоков

(11)

Рис. 4. Граф состояний многоканальной СМО

Условие существования стационарного режима: Р < 1. Остальные характеристики обслуживания n_i, l_i, u_i, определяются для каждого i-гo потока в отдельности по формулам (5)— (9).

Средние времена ожидания _ср и реакции u_ср по одной заявке из суммарного потока в системе связаны со средними количествами заявок в очереди и в системе следующими соотношениями:

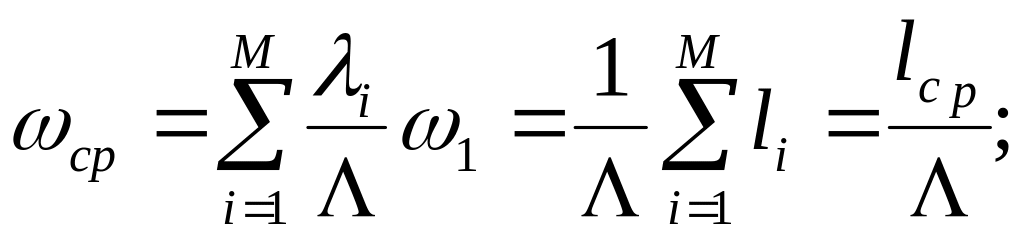(12)

(13)

где — суммарная интенсивность потоков; — вероятность того, что поступившая заявка является заявкой i-гo типа;

l_cp — средняя длина очереди заявок всех типов; n _ср — среднее число заявок всех типов в системе.

Многоканальная СМО. Предположим, что система имеет т обслуживающих каналов с одинаковой интенсивностью обслуживания , при общем простейшем потоке заявок с интенсивностью . Такая система условно обозначается М/М/т. Граф состояний этой системы (рис. 4) подобен графу одноканальной СМО. Интенсивности перехода в соседнее правое состояние определяются, как и у одноканальной СМО, интенсивностью входного потока : с приходом очередной заявки система переходит в следующее правое состояние. Иначе обстоит дело с интенсивностями у нижних стрелок. Пусть система находится в состоянии z₁ — работает один канал. Он производит обслуживании в единицу времени. Тогда . Представим, что система находится в состоянии z₂. Для перехода в состояние z₁ надо, чтобы закончил обслуживание первый или второй канал. Значит, суммарная интенсивность их обслуживания Суммарный поток обслуживания k каналами имеет интенсивность k . При k т интенсивность обслуживания сохраняется т . Получается модель размножения и гибели. Делая выкладки, как для одноканальной СМО, получим

Средняя длина очереди

(14)

Прибавляя к ней среднее число заявок, находящихся под обслуживанием, равное среднему числу занятых каналов

получим среднее число заявок в системе:

(15)

По формулам Литтла определяется среднее время пребывания заявки в очереди:

(16)

и в системе — время реакции:

(17)

В теории массового обслуживания имеются аналитические формулы для простейших СМО при одномерном и многомерном потоке заявок для одноканальных и многоканальных систем без ограничений и с ограничениями длин очередей.

Потоки обслуживания. При моделировании конкретных ВС потоки заявок и обслуживания могут отличаться от простейших. Потоки заявок могут быть, например, пуассоновскими или эрланговскими. Длительности обслуживания можно представить в общем случае гаммараспределением. Это распределение с плотностью вероятности

(18)

где — математическое ожидание длительности обслуживания М [ ]; k — параметр распределения (k 1); Г (k) — гамма-функция.

Дисперсия гамма-распределения

(19)

При k = 1 гамма-распределение вырождается в экспоненциальное. В пределе при k это распределение становится детерминированным с постоянной длительностью обслуживания . Параметр распределения k может быть определен по математическому ожиданию и дисперсии:

(20)

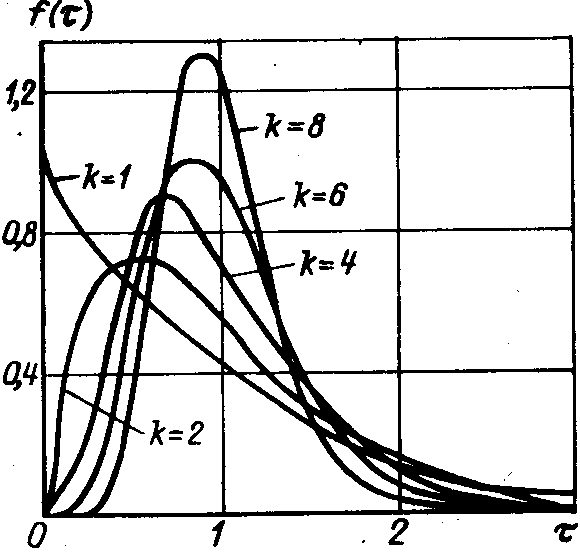
Рис. 5. Нормированное распределение Эрланга

При целочисленном k Г (k) = (k—1)!. Тогда из уравнения (18) имеем

, (21)

Это плотность нормированного распределения Эрланга k-го порядка. Вид распределения изображен на рис. 5. В данном распределении в отличие от потока Эрланга математическое ожидание не зависит от k и при k это распределение стремится к детерминированному, а не к нормальному.

В частных случаях длительности обслуживания могут быть распределены по экспоненциальному, равномерному, нормальному и другим законам. Для некоторых сочетаний законов распределений потоков заявок и обслуживании получены аналитические зависимости характеристик от параметров системы.

Системы с произвольным распределением длительности обслуживания. Представим, что моделью ВС является одноканальная СМО с неограниченной очередью. В эту систему поступает простейший поток заявок с интенсивностью . Заявки обслуживаются в порядке поступления. Длительность обслуживания имеет произвольное распределение с математическим ожиданием и коэффициентом вариации . Такая система обозначается M/G/1. В этой системе в установившемся режиме среднее число заявок в очереди

(26)

среднее число заявок в системе

(27)

Последние два выражения называются формулами Поллачека—Хинчина. Средние времена пребывания заявок в очереди и в системе определяются по формулам Литтла.

Для системы M/G/1 могут быть аналитически определены дисперсии выходных характеристик. Подобные формулы известны также для случая многомерного простейшего потока заявок.

Системы с отказами. Предположим, что на ВС, представленную как m-канальная СМО, поступает простейший поток заявок с интенсивностью К. Поток обслуживания имеет произвольный закон распределения с интенсивностью р. Это система M/G/m. При этом очередная заявка, поступившая в систему, когда все каналы заняты, покидает ее без обслуживания. Это означает, что очереди в системе отсутствуют. Характеристиками такой системы могут служить пропускная способность, вероятность обслуживания и среднее число занятых каналов. Данная система соответствует модели размножения и гибели. На основании формул (13) и (14) (лекция 9) можно вывести вероятность того, что в СМО находится т заявок, т. е. все каналы заняты:

(28)

Вероятность того, что очередная заявка будет обслужена,

(29)

Пропускная способность системы определяется как среднее число заявок, обслуживаемых в единицу времени;

(30)

а среднее число занятых каналов определяется по формуле

(31)

Системы с приоритетными дисциплинами диспетчеризации.

В теории вычислительных систем детально изложены и исследованы аналитические зависимости характеристик от параметров ВС, представленных моделями СМО с ординарными и неординарными, одномерными и многомерными потоками заявок, обслуживаемых одноканальными и многоканальными приборами с произвольными законами распределения длительности обслуживания и различными дисциплинами диспетчеризации, включая системы с относительным, абсолютным, смешанным и динамическим приоритетами.

Например, допустим, что в СМО поступает М типов простейших потоков с интенсивностями и длительности обслуживания заявок каждого потока имеют математические ожидания и дисперсии . системе используется смешанная дисциплина диспетчеризации с тремя классами: 1) заявкам типов 1,..., M₁ присвоены абсолютные приоритеты по отношению к заявкам второго и третьего классов; 2) заявкам типов M₁+1,..., M₁+M₂ — относительные приоритеты по отно­шению к заявкам третьего класса; 3) заявки типов M₁+M₂++1,..., M обслуживаются в порядке поступления. Среднее время ожидания заявок различных типов определяется из выра­жения:

(32)

где

Из формулы (32) могут быть получены как частные случаи

характеристики систем с абсолютными ( , относи­тельными (М₁ = M₃ = 0) и смешанными приоритетами с двумя классами заявок: с абсолютными и относительными приорите­тами (М₃ = 0), с абсолютными приоритетами и без приоритетов (М₂ = 0), с относительными приоритетами и без приоритетов (M₁ = 0).