1. Расшифровка дифрактограмм

В результате съемки на ДРОН-3М получаем дифрактограмму. Дифрактограмма характеризуется наличием рефлекса, его высотой, углом. Результаты рентгенофазового анализа обрабатывают и заносят в таблицу:

№ линии

h,мм

J/J0

q°

d,A

1/d2

h k l

В процессе исследования получают вещества, известные в практике, для которых в литературе имеются сведения о сингонии и параметрах кристаллической решетки.

В этом случае по известным параметрам составляют массив значений 1/d² теор; сравнивая 1/d² теор. и 1/d² эксп., присваивают рефлексам значения hkl, а затем находят параметры решетки для синтезированного образца в зависимости от структуры решетки [8].

5 Магнитные характеристики материалов

Под магнитными свойствами вещества подразумевается способность тел (движущихся в них частиц) взаимодействовать с магнитным полем.

Первопричина этих свойств — внутренние скрытые формы движения электрических зарядов, представляющие собой элементарные круговые токи. Такими токами являются спины электронов и их орбитальное вращение в атомах. Им соответствуют спиновые и орбитальные магнитные моменты атомов, которые и определяют магнитные свойства твердых тел [3].

Согласно квантовой механике, магнитный орбитальный момент электрона выражается формулой:

μ_l^эл = - μ_Б√(l(l+1), (5.1)

где l — орбитальное квантовое число (l = 0, 1, 2... n - 1).

Проекция его на направление внешнего магнитного поля равна:

μ_lτ^эл = m_lμ_Б, (5.2)

где m_l — магнитное квантовое число (m_l = 0, ±1, ±2, … ±l);

μ_Б = eħ/2mc магнетон Бора (е — заряд электрона, m — масса электрона, с — скорость света, ħ — постоянная Планка).

Магнитный спиновый момент электрона выражается формулой:

μ_s^эл = -2μ_Б √S(S+1)= -μ_Б√3, (5.3)

где S=1/2 — спиновое квантовое число электрона.

Проекция его на ось квантования z равна:

μ_sz^эл = gSμ_Б ≈ μ_Б, (5.4)

где g — фактор спектроскопического расщепления, для свободного электрона g=2,0023.

Поскольку атомы могут содержать более одного электрона, в них находят суммарные орбитальный и спиновый магнитные моменты электронов, используя квантовые числа l и S [3].

Если поместить изотропное тело объемом V в однородное магнитное поле напряженностью H и индукцией B₀=ϻ₀H (ϻ₀ — магнитная проницаемость вакуума), то под действием этого поля тело будет намагничиваться, приобретая магнитный момент ϻ. Магнитный момент единицы объема данного тела:

I_m = M/V = lim 1/V ∑ μ_mi, (5.5)

где N — число атомов в объеме тела, μ_mi - магнитный момент і-го атома (частицы).

Намагниченность является векторной величиной. В изотропных магнитных материалах вектор I_m направлен параллельно или антипараллельно Н. Отношение I_m к Н поля характеризует объемную магнитную восприимчивость материала χ_m:

χ_m = I_m /H_m (5.6)

Величина χ_m является безразмерной и характеризует связь намагниченности вещества с его магнитным полем. В переменных магнитных полях, χ_m - комплексная величина. Она может быть как положительной, так и отрицательной [3].

Если намагниченное тело находится во внешнем магнитном поле Н (В_o), то в нем возникает собственное (внутренне) магнитное поле В_і = χ_mВ_o = χ_mϻ₀H, которое в изотропных материалах направлено параллельно или антипараллельно внешнему полю В_o. Результирующее поле в материале характеризуется магнитной индукцией В:

B = B_o + B_i ≈ ϻ₀(1+χ_m)H = ϻ₀ μH = ϻB₀ = ϻ₀(H+I_m), (5.7)

где величина ϻ = 1+χ_m — относительная магнитная проницаемость материала, она показывает, во сколько раз В в данном материале отличается от В_o в вакууме; ϻ = В/ϻ_o H, т.е. характеризует изменение В материала при воздействии магнитного поля Н и является безразмерной величиной [3].

В анизотропных кристаллах векторы В и Н неколлинеарны, поэтому ϻ и

χ_m - тензорные величины (полярные тензоры второго ранга). Тогда соотношения (5.6) и (5.7) следует записать в виде І_і = χ_іjH_j и В_і = ϻ_іjН. В переменных магнитных полях имеют делать с динамической магнитной проницаемостью, когда на намагниченность материала оказывают влияние вихревые токи и другие явления; как и χm она представляет собой комплексную величину. В ферромагнетиках χm и ϻ очень сложно и сильно зависит от Н, поэтому для них вводят понятие о дифференциальной магнитной восприимчивости и магнитной проницаемости.

Если намагничиванию подвергается тело незамкнутой формы, то на его поверхности в направлении внешнего поля возникают «магнитные заряды», создающие дополнительное магнитное поле Н_д. Его называют размагничивающим полем, в первом приближении пропорциональном величине намагниченности Н_д = -NI_m, где N — так называемый размагничивающий фактор, зависящий от формы тела. При учете размагничивающего поля суммарное истинное поле внутри тела, фактически вызывающее появление намагниченности I_m будет:

H = H_b + H_д = H_{b –} Ni_m , (5.8)

где через H_b обозначено внешнее магнитное поле. Учет размагничивающего поля существенен лишь для сильномагнитных веществ (например, ферромагнетиков), для которых величина I_m сравнима с внешним полем. Поле Нд однородно только в телах, имеющих эллептическую форму [3].

Подставляя равенство (5.8) в (5.6), получаем:

I_m = χ_mH = H_b χ_m/1+χ_mN = χ_оH_b, (5.9)

где χm, χ_о - восприимчивость соответственно вещества и тела.

В зависимости от величины и знака магнитной восприимчивости χ все материалы традиционно делят на три группы: диа- пара и ферромагнитные.

Диамагнитные вещества имеют низкую (~10^-5) отрицательную магнитную восприимчивость, мало зависящую от температуры. Диамагнетизм связан с орбитальным движением электронов и является прямым следствием закона Ленца. Индуцированный движением электронов магнитный момент направлен противоположно магнитному полю. Диамагнетизм присущ всем веществам, однако во многих телах он подавляется более сильными эффектами пара- и ферромагнетизма. Типичными представителями диамагнетиков являются инертные газы, многие органические соединения и некоторые металлы (медь, серебро, барий, золото и др.).

Парамагнитные вещества обладают положительной магнитной восприимчивостью, зависящей от температуры. При комнатной температуре величина χ весьма мала (~10^{-3 —} 10^-6) [3].

Парамагнетизм наблюдается у веществ, атомы которых имеют нескомпенсированные спины, т.е. обладают постоянными магнитными моментами. В отсутствии магнитного поля такие вещества немагнитны из-за беспорядочного распределения атомных магнитных моментов. При наложении магнитного поля атомные магнитные моменты устанавливаются вдоль его направления, преодолевая дезориентирующее действие теплового движения. Типичными парамагнетиками являются щелочные металлы, много численные соли редкоземельных элементов, а также газы: кислород, оксид (I) азота и др.

Ферромагнетики — спонтанно намагниченные вещества, представляющие собой систему взаимодействующих атомов или ионов. Эти вещества характеризуются положительной и относительно большой по величине магнитной восприимчивостью. Температурная зависимость χ нелинейна.

Ферромагнитные вещества обладают магнитным моментом и в отсутствии внешнего поля при температурах ниже температуры температуры Кюри [3].

Значение магнитной восприимчивости для некоторых диа-, пара - и ферромагнитных материалов приведены в таблице 5.1.

Спонтанная намагниченность в ферромагнетиках возникает благодаря связи между спиновыми магнитными моментами. Воздействия спинов могут приводить к двум видам упорядочения, соответствующим минимуму энергию. Эти упорядочения отвечают параллельному (ферромагнетизм) и антипараллельному (антиферромагнетизм) расположению спинов.

Антиферромагнетики, в свою очередь, могут быть скомпенсированы ми или нескомпенсированными. Последние носят также название ферримагнетиков [3].

Таблица 5.1 Значение магнитной восприимчивости некоторых материалов

в слабом магнитном поле при 293 К.

Диамагнетики	χm ,10-6	Парамагнетики	χm ,10-6	Ферромагнетики	χm
Висмут	-284	Платина	189	Железо	1000
Серебро	-21.5	Титан	161	Никель	240
Цинк	-11.4	Вольфрам	55	Кобальт	150
Медь	-5.4	Алюминий	17
Кремний	-3	Магний	13,02

Таким образом, если вещество обладает нескомпенсированными спинами, оно является пара-, ферро-, или антиферромагнетиком. При параллельной ориентации магнитных моментов вещество представляет собой ферромагнетик, при антипараллельной — антиферромагнетик или ферримагнетик в зависимости от соотношения между величинами антипараллельных магнитных моментов (рис. 5.1).

Одной важнейших характеристик магнитных материалов является кривая намагничивания, представляющая собой зависимость магнитной индукции В (или намагниченности І) предварительно размагниченного образца от напряженности внешнего магнитного поля Н. При циклическом перемагничивании кривая В(Н) образует петлю гистерезиса (рис. 5.2).

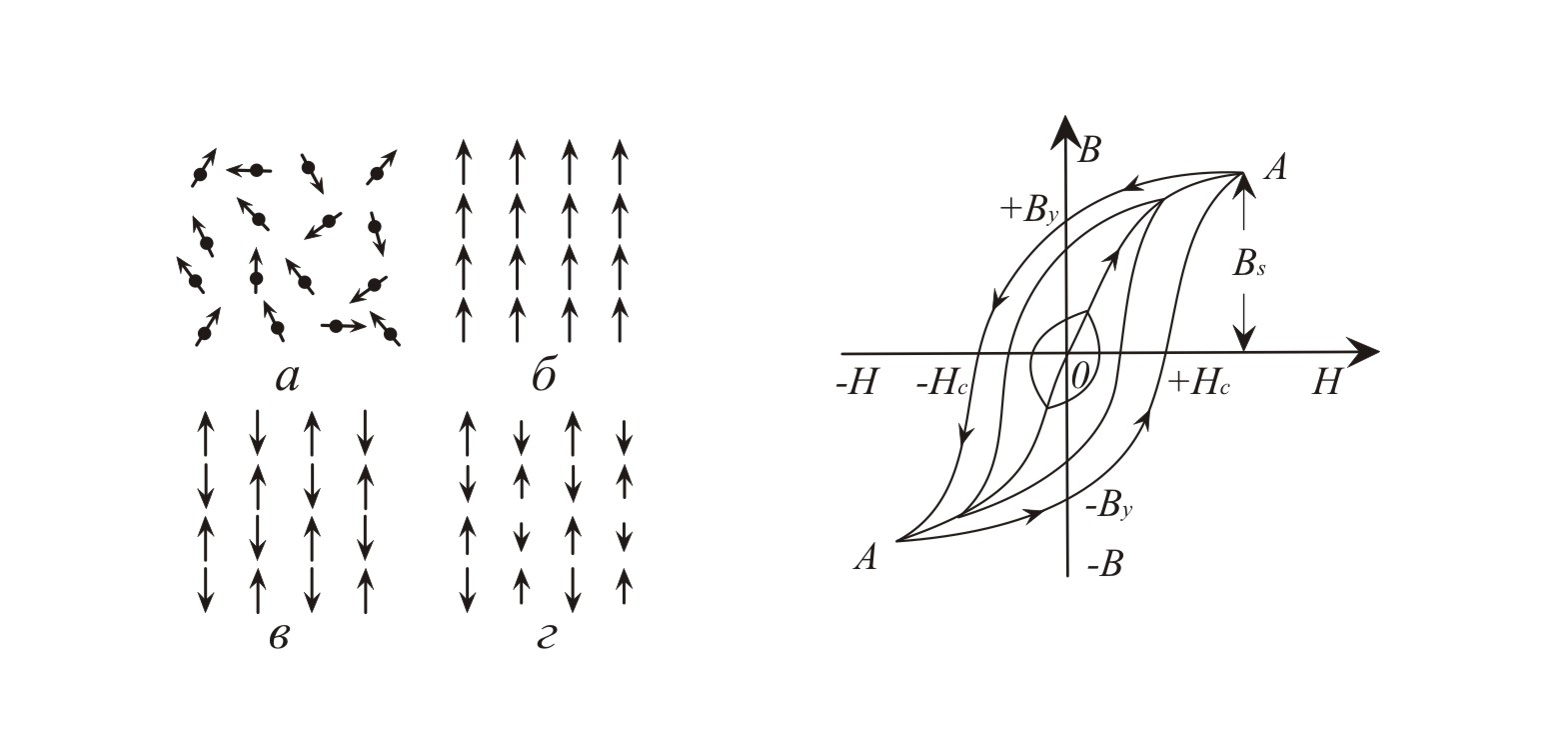
Рис. 5.1 Схематическое изображение величины и направления элементарных магнитных моментов в пара- (а), ферро- (б), антиферро- (в)

и ферримагнетиках (г)

Рис. 5.2 Кривая намагничивания

Если уменьшить Н внешнего поля ферромагнетика, намагниченного до насыщения (кривая 0А на рис. 5.2), то В будет уменьшаться по кривой AB_r (-H_c) и при Н = 0 у образца сохраняется так называемая остаточная индукция B_r . Для ее устранения необходимо приложить размагничивающее поле Hc противоположного направления, которое называется коэрцитивной силой. При дальнейшем увеличении магнитного поля обратного направления, образец вновь намагничивается вдоль поля до насыщения (точка А′). Перемагничивание образца (А′ → А) происходит по кривой А′(-B_r)H_cА. Таким образом, при перемагничивании происходит отставание изменения В от изменения Н, т.е. наблюдается магнитный гистерезис. Замкнутую кривую АВ_r(-H_c)А′(-В_r)H_cА, описывающую полный цикл перемагничивания ферромагнетика, называют магнитной петлей гистерезиса. Площадь петли пропорциональна работе перемагничивания единичного объема ферромагнетика, которая переходит в теплоту. Поэтому в высокочастотных магнитных полях ферромагнетики могут сильно нагреваться [3].

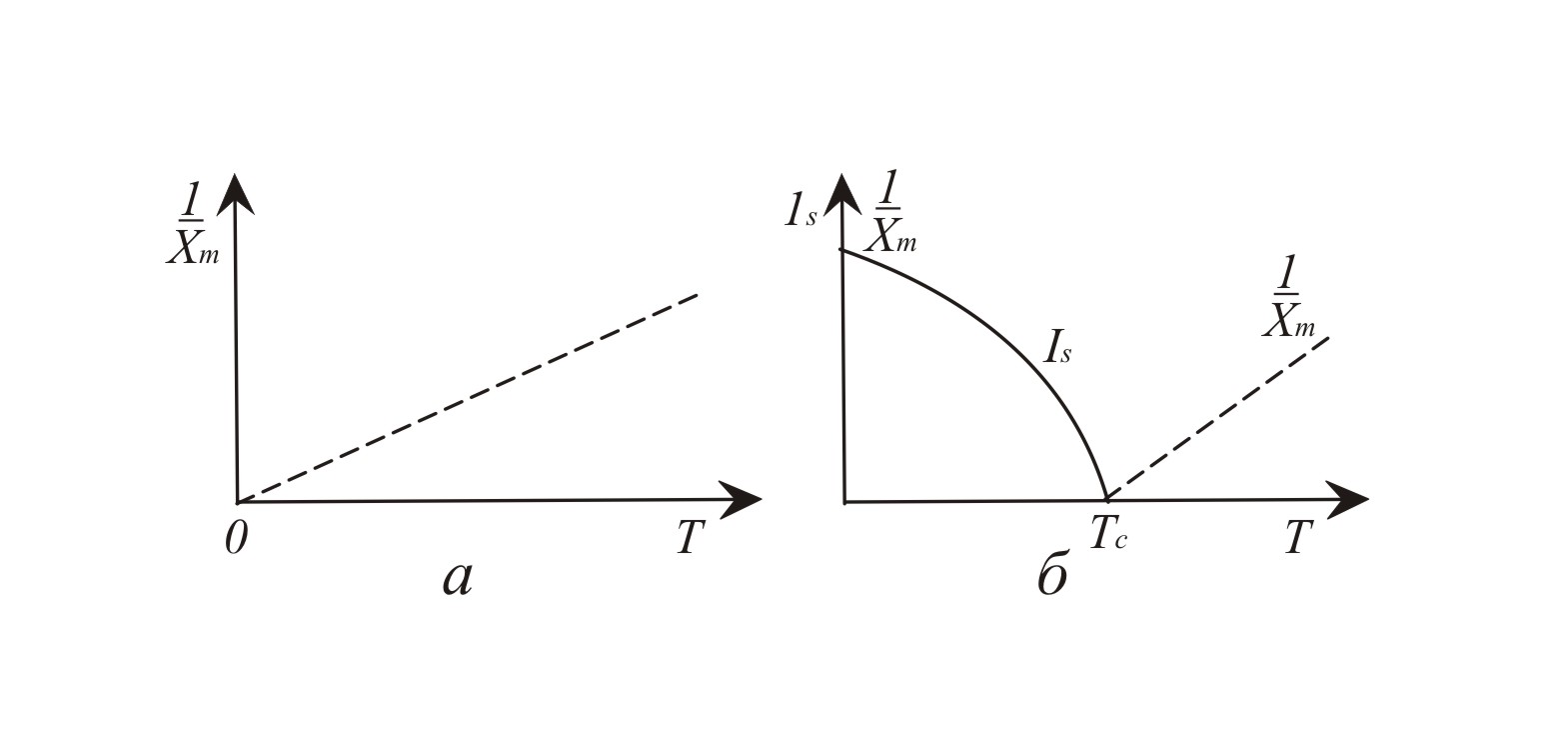
Рис. 5.3 Зависимость магнитной восприимчивости от температуры для парамагенетиков (а) и намагниченности насыщения для ферромагнетиков (б)

При нагревании ферромагнитных материалов их магнитные свойства χ_m, μ и I_s уменьшаются. Для каждого ферромагнетика существует температура Т_с называемая ферромагнитной точкой Кюри, при которой он утрачивает свои ферромагнитные свойства. При температуре выше Т_с ферромагнетик становится парамагнетиком, испытывая фазовый переход ІІ рода. При этом χ_m парамагнетика изменяется с изменением температуры (рис. 5.3, б) по закону Кюри- Вейса:

χ_m=C/T- Т_с (5.10)

Аналогичный закон имеет место в случае сегнетоэлектриков. Для железа

Тс =770◦С, для кобальта 1150◦С, для никеля 360◦С [3].