15. Статическая проверка расчетных эпюр

Для проверки правильности построенных эпюр М_рас, , составляются условия статического равновесия всей рамы. В заданной раме отбрасываются все опорные стержни, а вместо них прикладываются внутренние усилия, взятые с расчетных эпюр (моменты с М_рас, поперечные силы с Q_рас, продольные усилия с ). Если эпюры построены верно, то сумма проекций на вертикальную и горизонтальную оси и сумма моментов относительно любой точки всех опорных реакций и внешней нагрузки должны равняться нулю:

(16)

16. Построение расчетных эпюр другим способом

Эпюры М_рас, , могут быть построены по иному. Для этого к основной системе прикладываются найденные в п. 10 неизвестные усилия и заданная нагрузка. В полученной статически определимой раме

определяются опорные реакции, затем внутренние усилия методом сечений и строятся расчетные эпюры изгибающих моментов, поперечных и продольных сил. Этот способ удобно применять для контроля правильности построения эпюр, если не выполняются деформационная и статическая проверки.

Пример расчета рамы

Для статически неопределимой рамы, показанной на рис. 9, требуется построить эпюры внутренних усилий от заданной нагрузки.

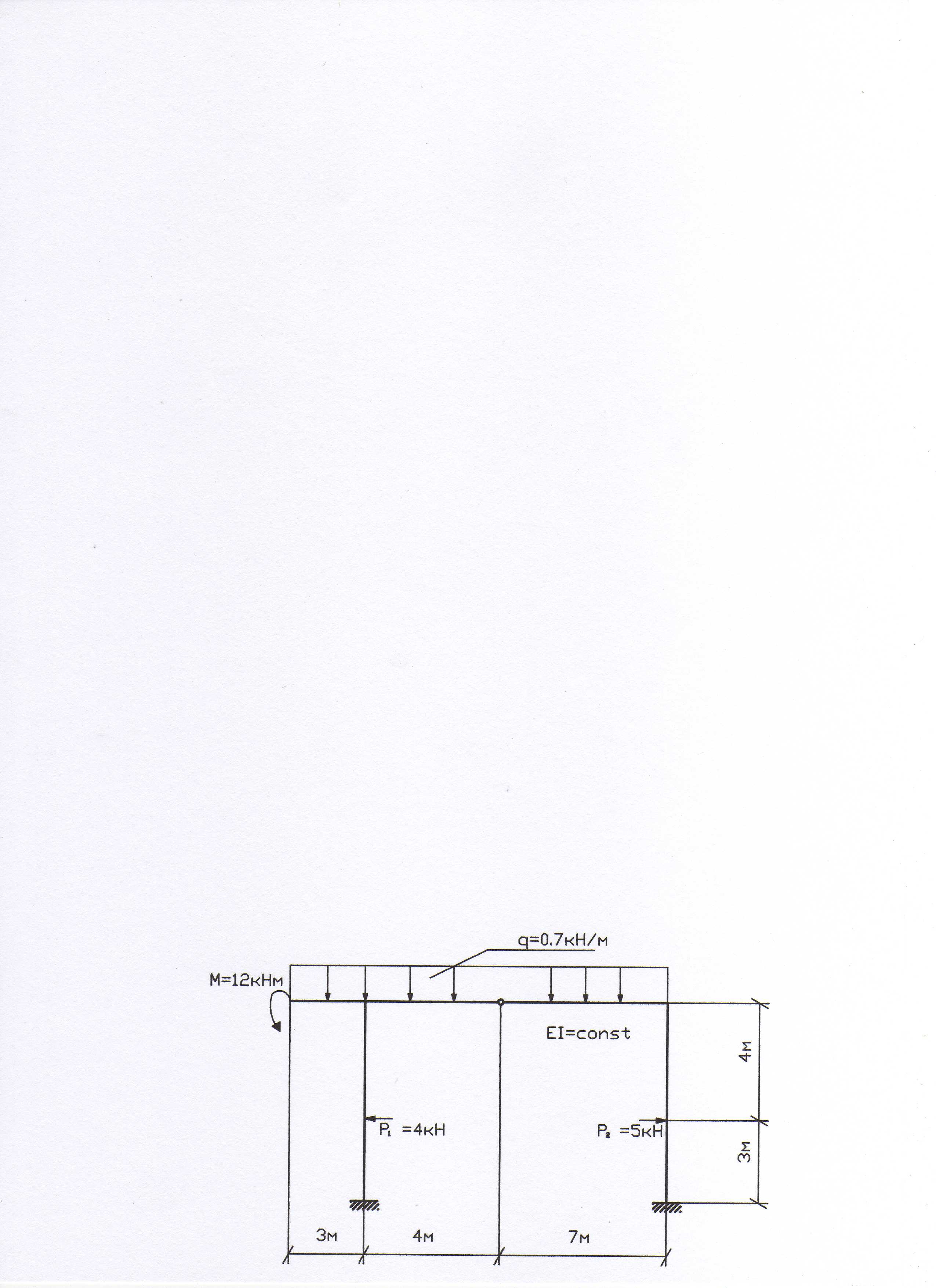
Рис. 9

1. Определяем степень статистической неопределимости рамы по формуле (8):

n = – 3 – Ш =6 – 3– 1=2,

Данная рама дважды неопределима.

2. Выбираем основную систему (рис. 10).

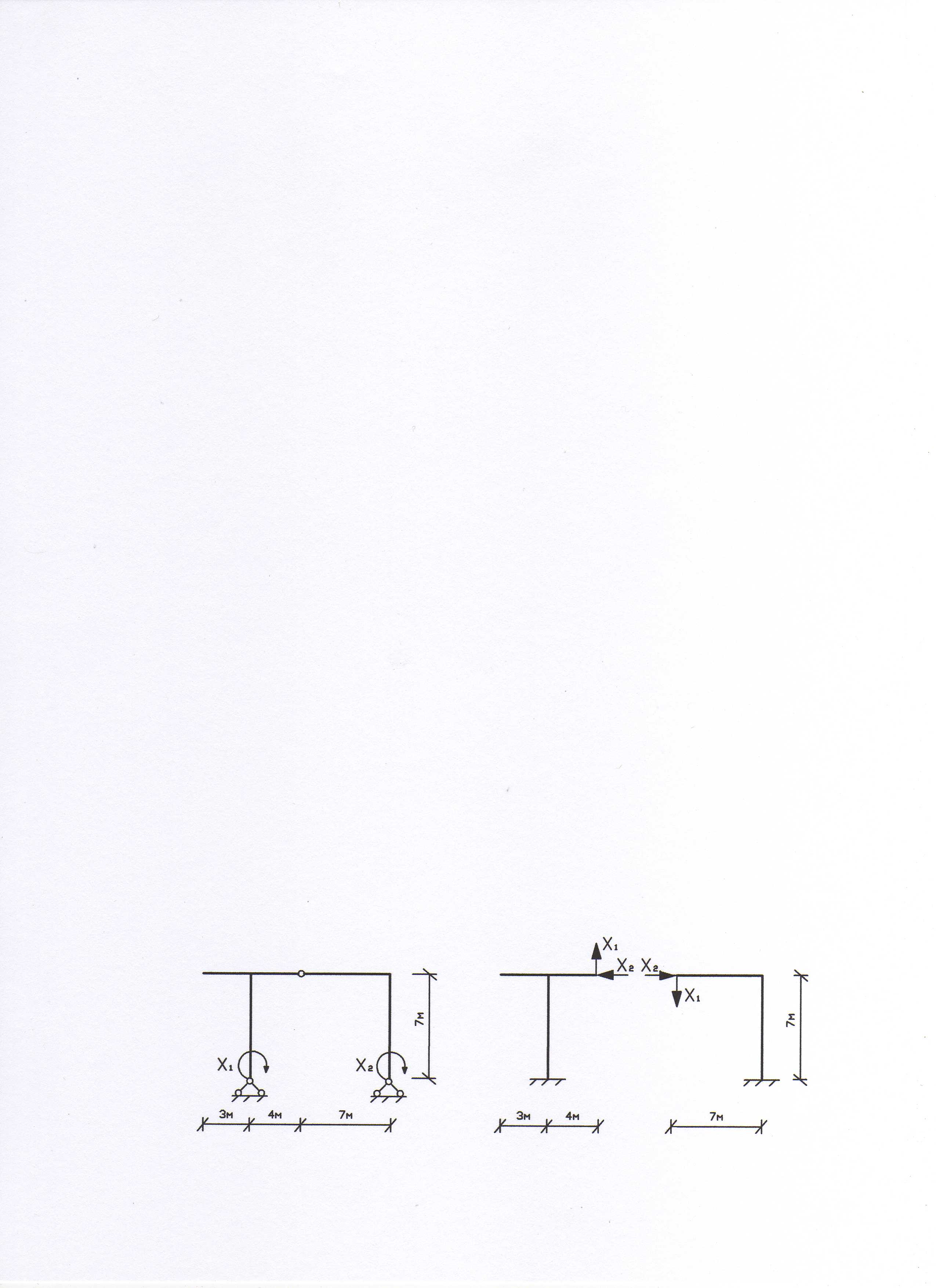
Вариант 1 Вариант 2 Рис. 10

К расчету выберем вариант 1 основной системы, т.к. он не требует определения опорных реакций (рис. 11)..

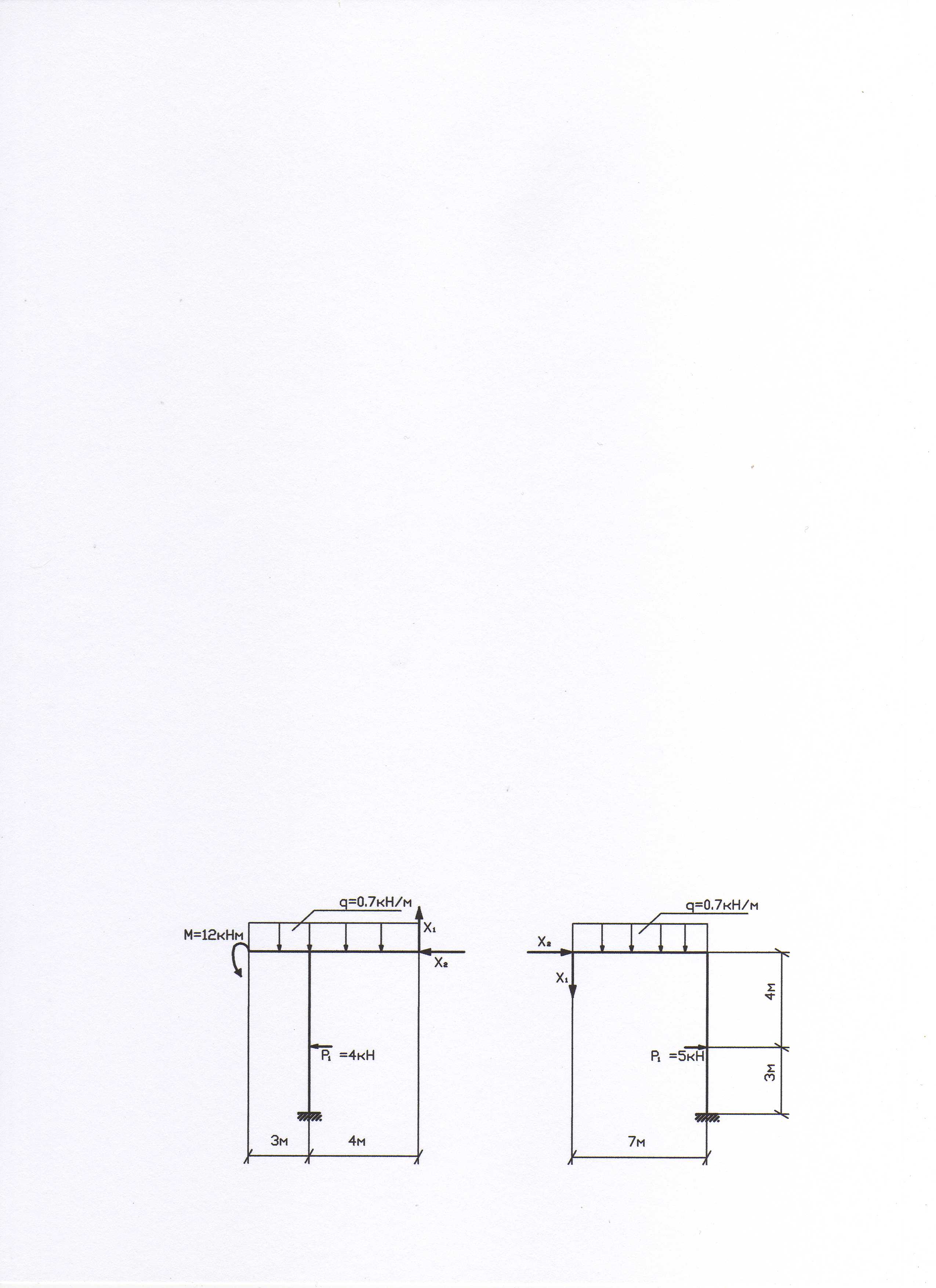
Рис. 11

3. Для определения неизвестных составляем каноническое уравнение метода сил

4. Строим единичные эпюры последовательного приложения сил и (рис. 12).

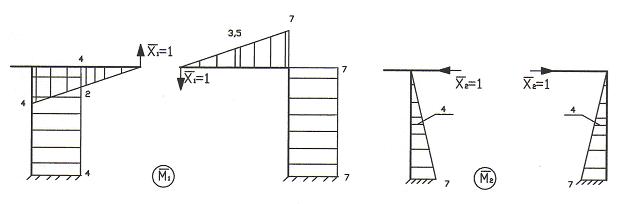
Рис. 12

5. Определяем главные и побочные коэффициенты канонических уравнений по интегралу Мора (2), с помощью способа Верещагина:

;

;

.

6. Делаем проверку правильности вычисления коэффициентов. Для этого построим суммарную единичную эпюру моментов (рис. 13) и вычислим по формуле (4) с помощью способа Верещагина и трапеций:

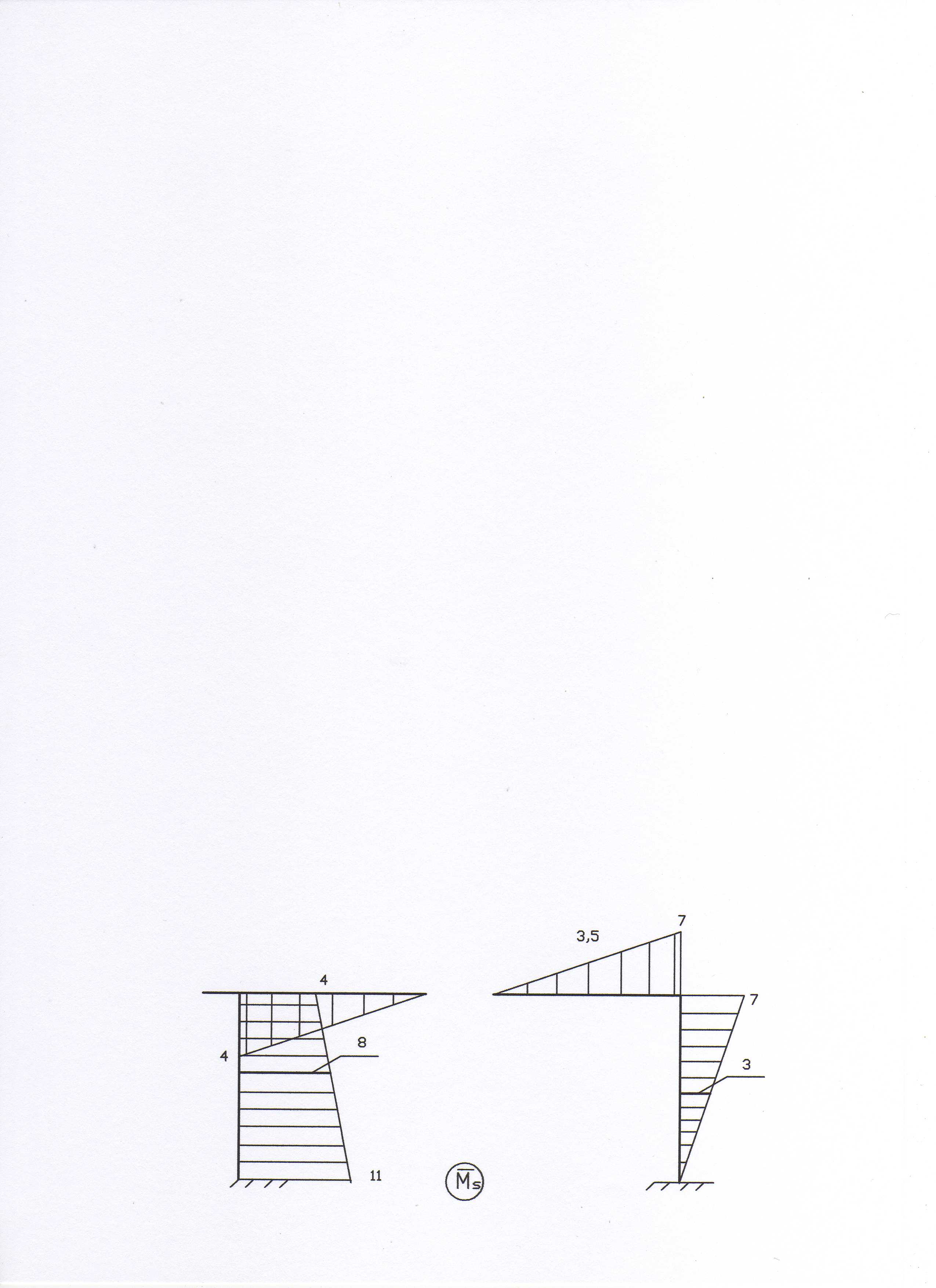
Рис. 13

;

.

Проверка выполнилась.

7. Строим грузовую эпюру изгибающих моментов в основной системе от действия только внешней нагрузки (рис. 14), отдельно прикладывая q и P, M.

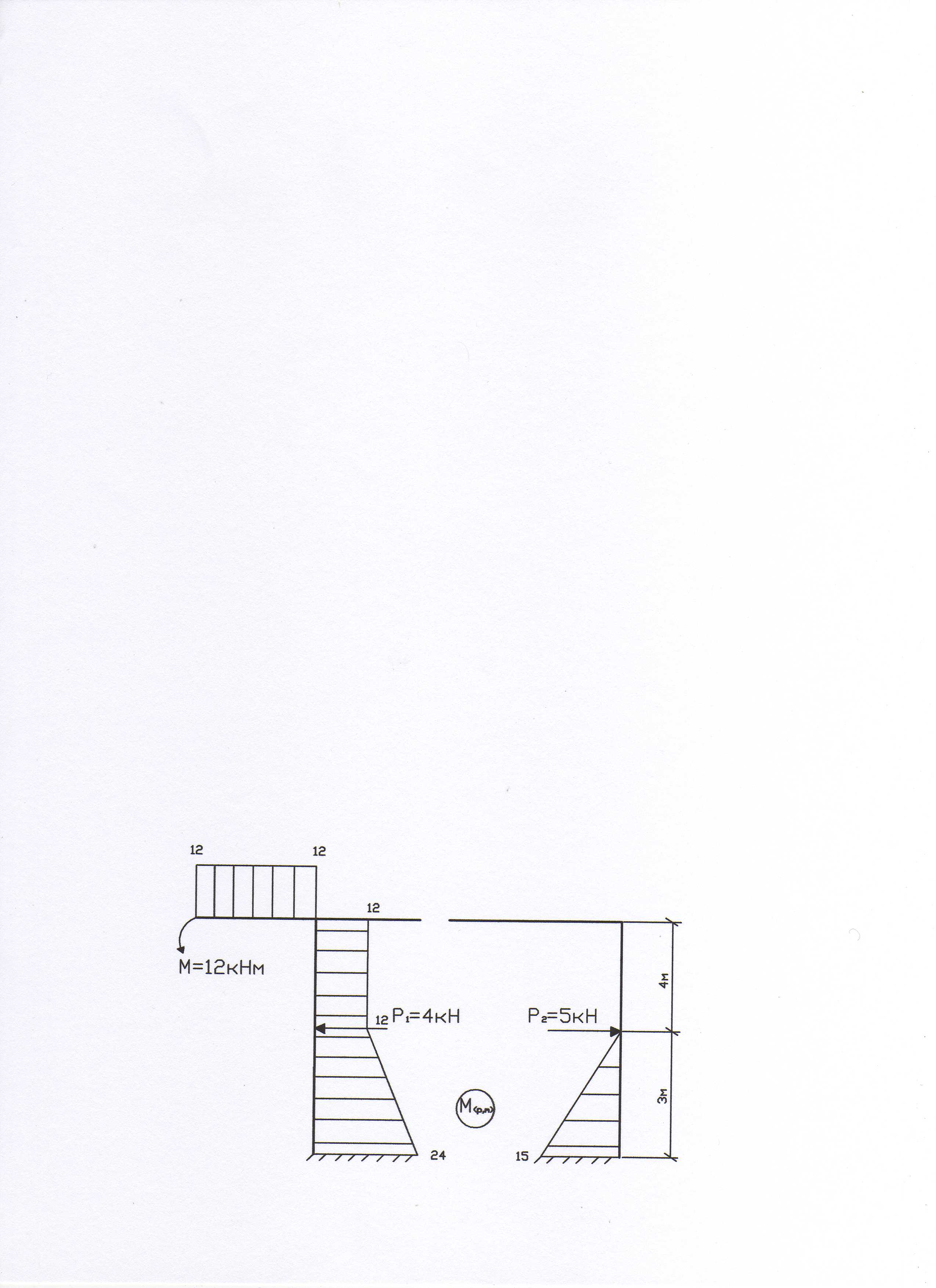
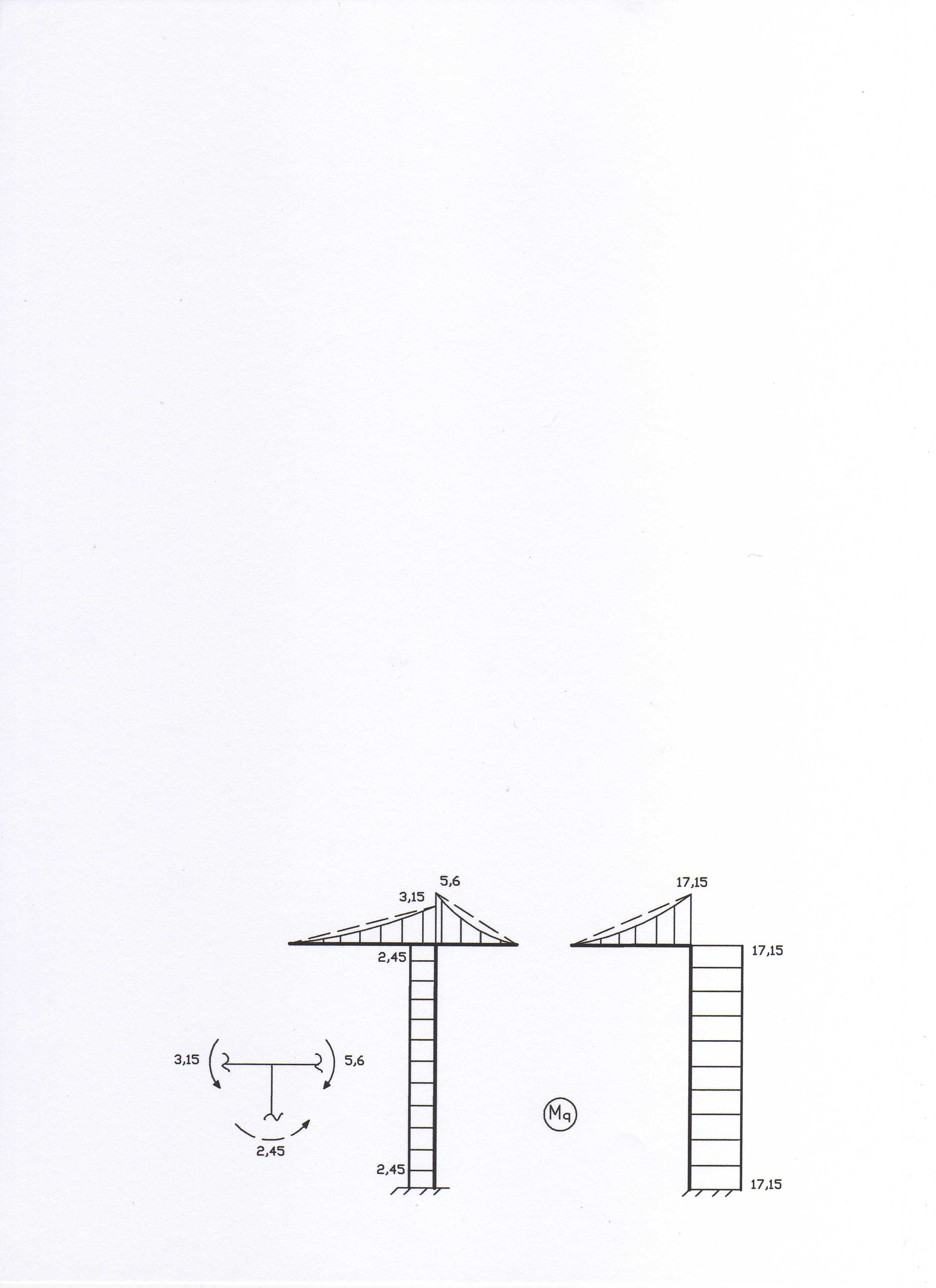
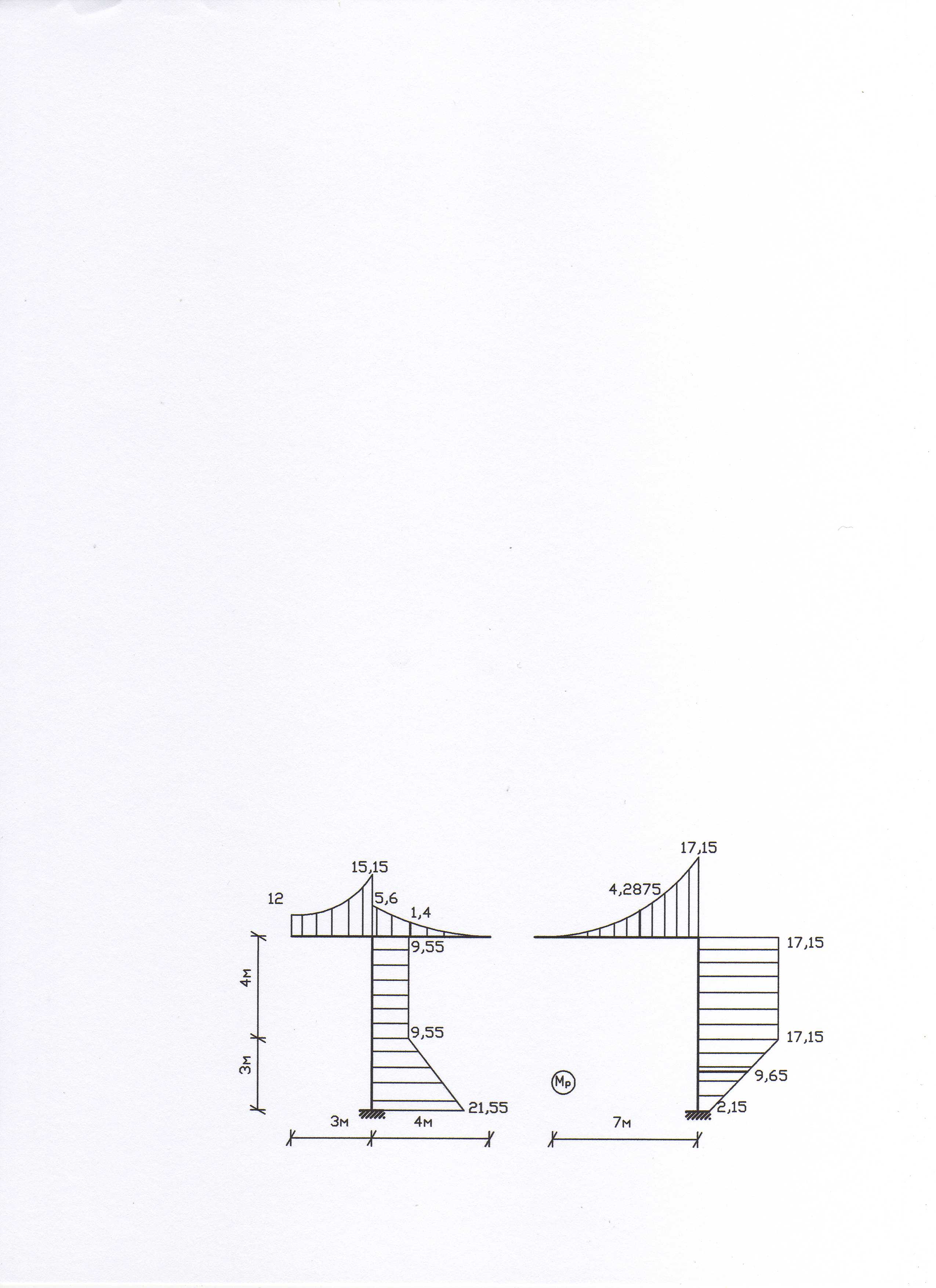
Рис. 14

8. Определяем грузовые коэффициенты канонических уравнений по формуле (3) способом Верещагина, используя формулы Симпсона и трапеций:

9. Проверяем правильность вычисления грузовых коэффициентов по формуле (5):

.

Проверка выполнилась.

10. Составляем и решаем систему канонических уравнений.

=>

Проверка:

Погрешность допустима за счет сокращений.

11. Для построения окончательной эпюры моментов строим исправленные эпюры и (рис. 15).

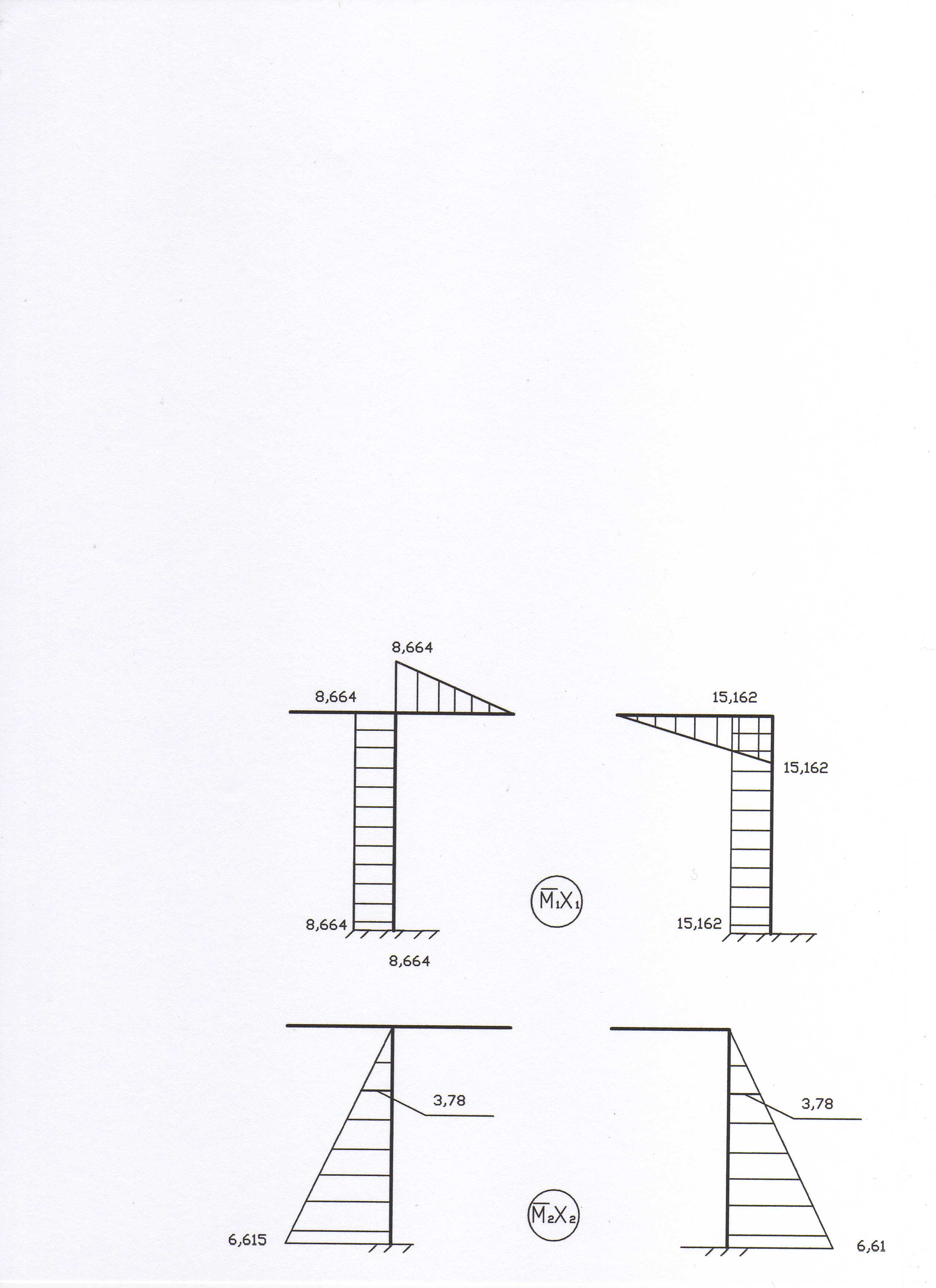
Рис. 15

Расчетную эпюру моментов (рис. 16) строим по формуле

.

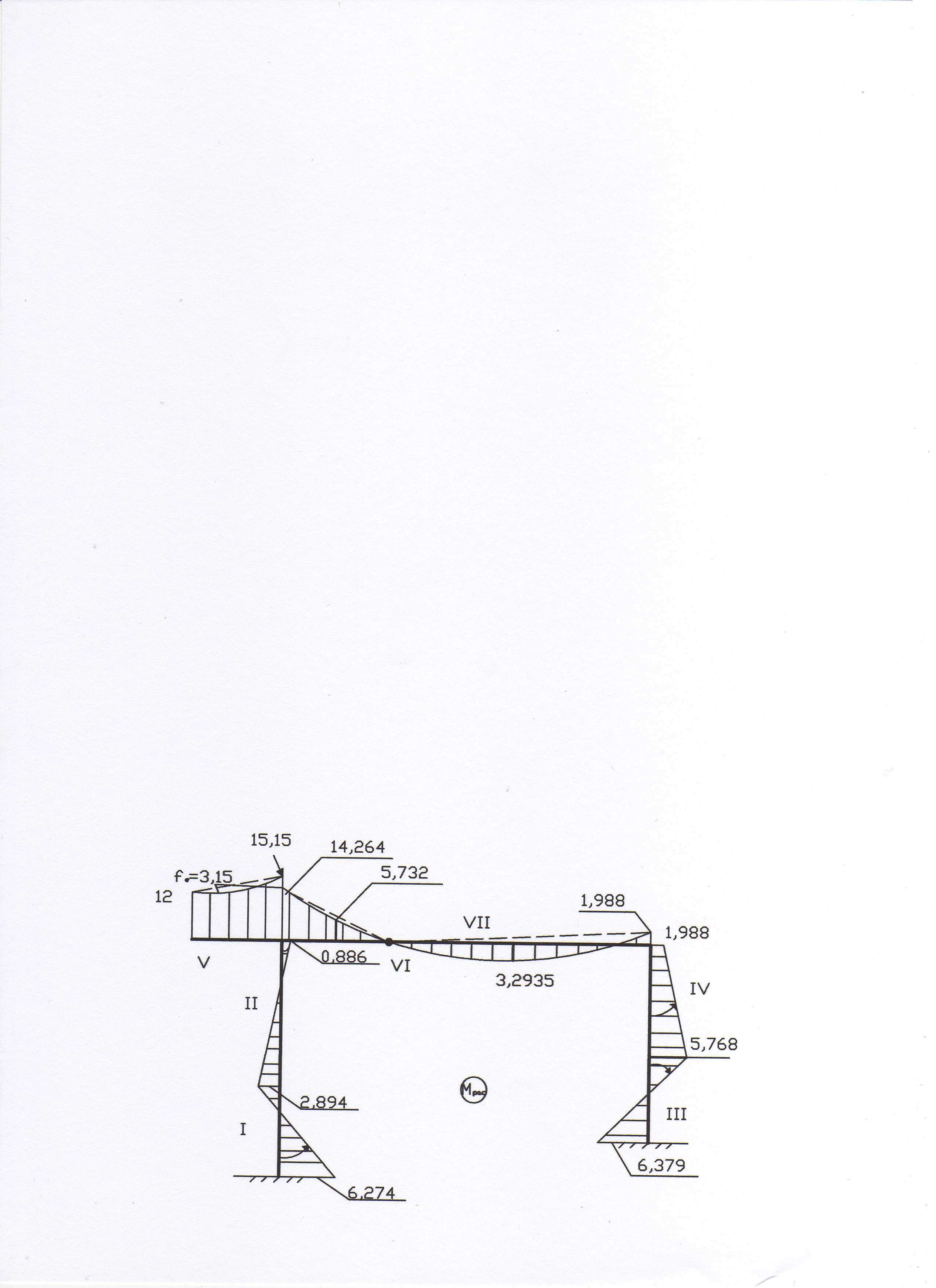
Рис. 16

Делаем узловую проверку построенной эпюры

.

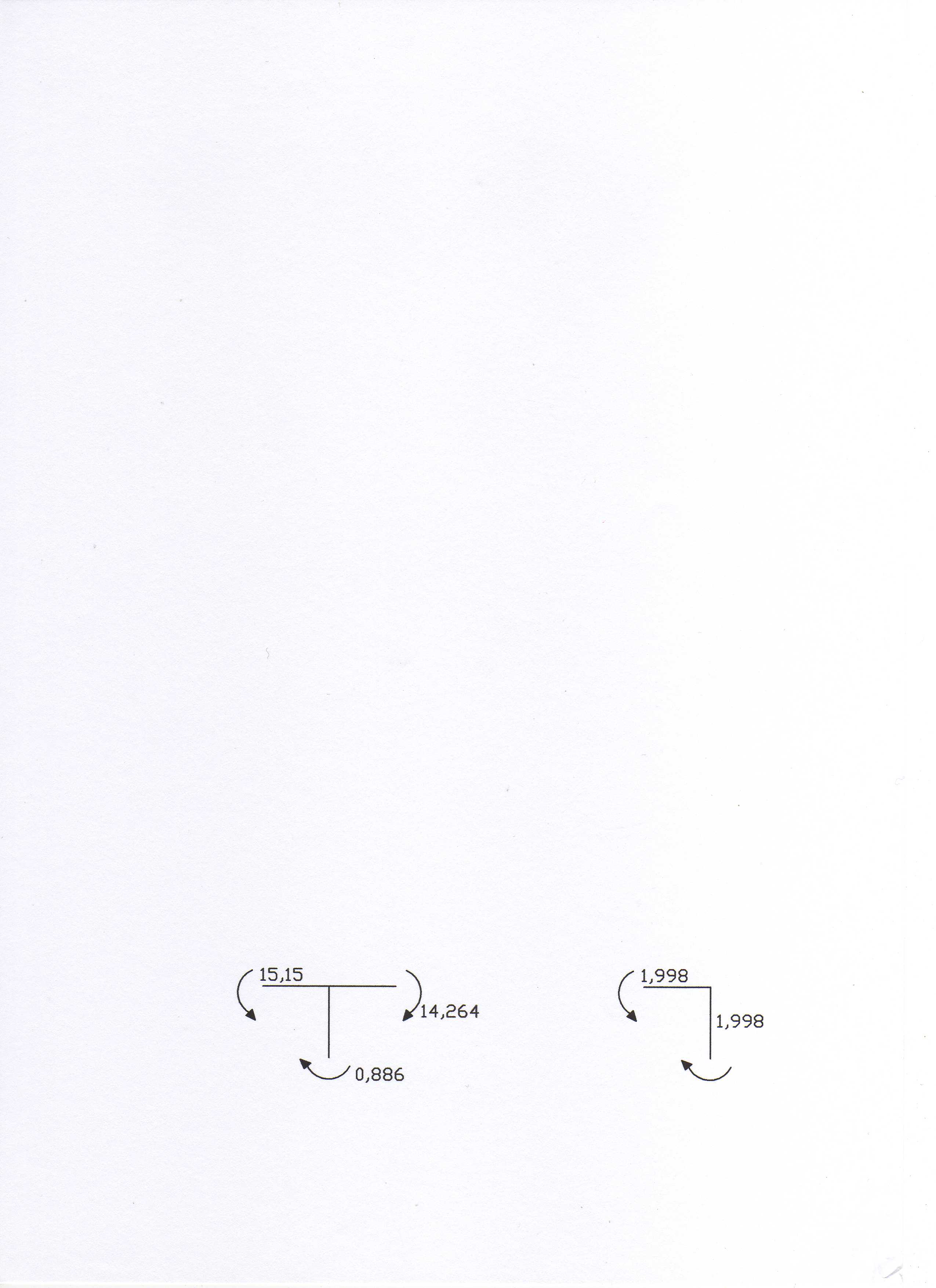
Проверка выполнилась, узлы находятся в равновесии.

12. Делаем деформационную проверку , для чего строим суммарную единичную эпюру моментов (рис. 17) в другом варианте основной системы.

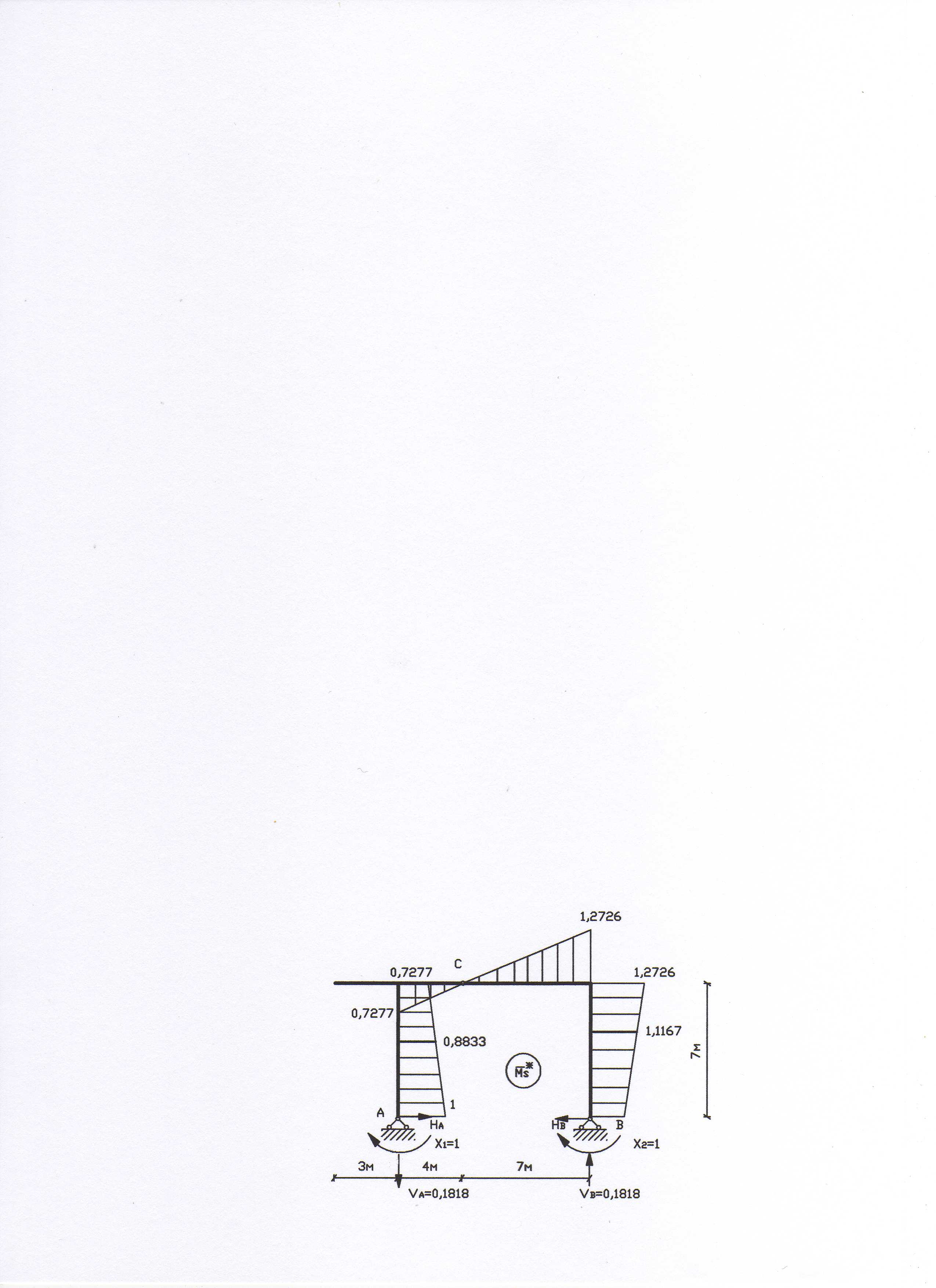
Рис. 17

Погрешность 0.18%. Проверка выполнилась. Расчетная эпюра моментов построена верно.

13. По эпюре строим расчетную эпюру поперечных сил по участкам.

I участок:

.

II участок:

.

III участок:

.

IV участок:

На остальных участках действует распределенная нагрузка, поэтому поперечную силу вычисляем в соответствии с рис. 18.

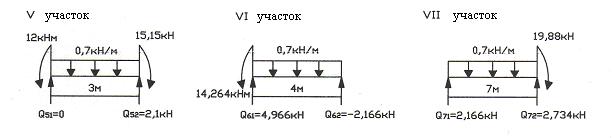
Рис. 18

Строим эпюру (рис. 19) по полученным данным и правилам знаков для внутренних усилий в балках.

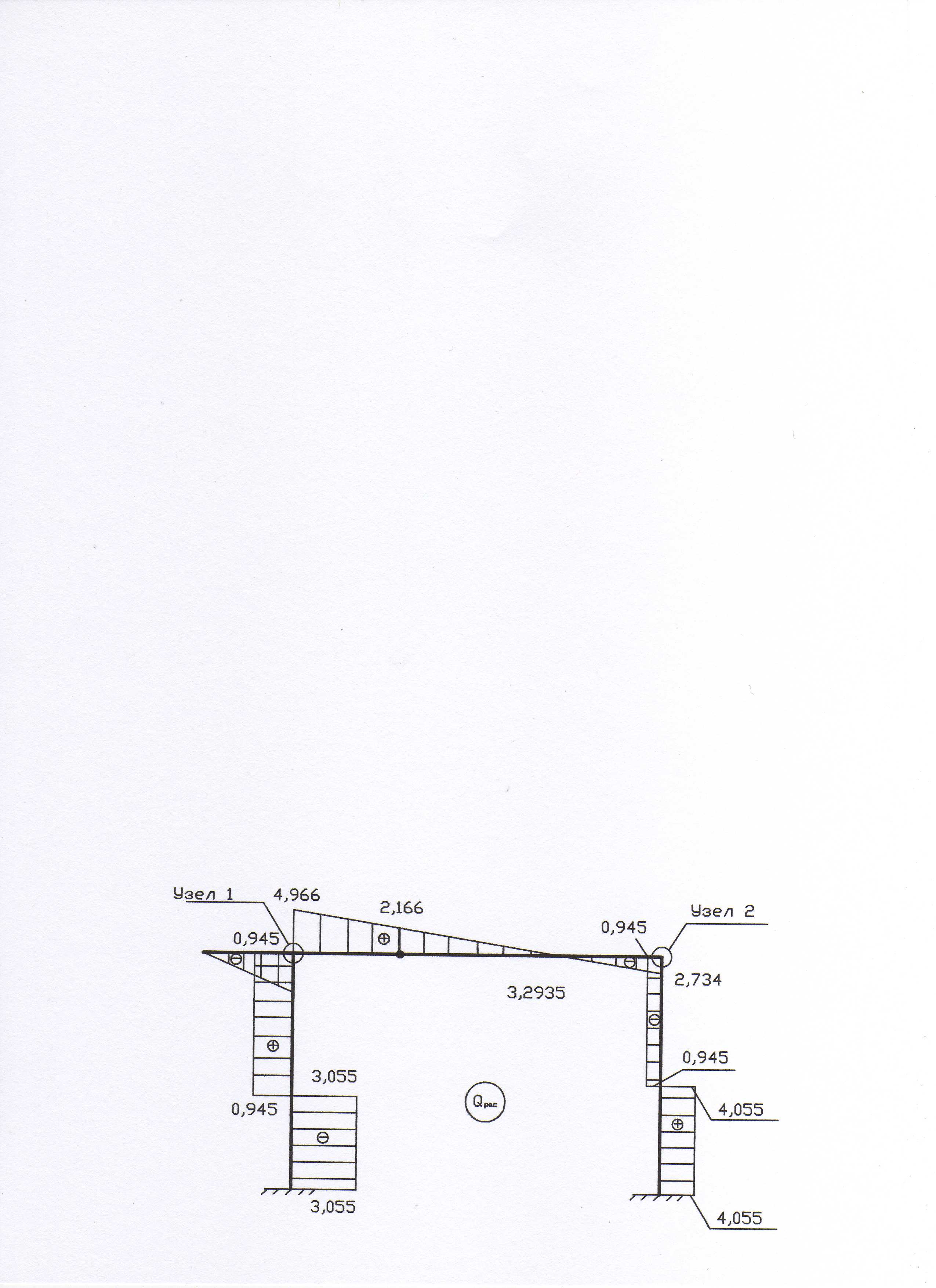
Рис. 19

14. Строим расчетную эпюру продольных усилий (рис. 20) по эпюре методом вырезания узлов.

: , : ,

: . : .

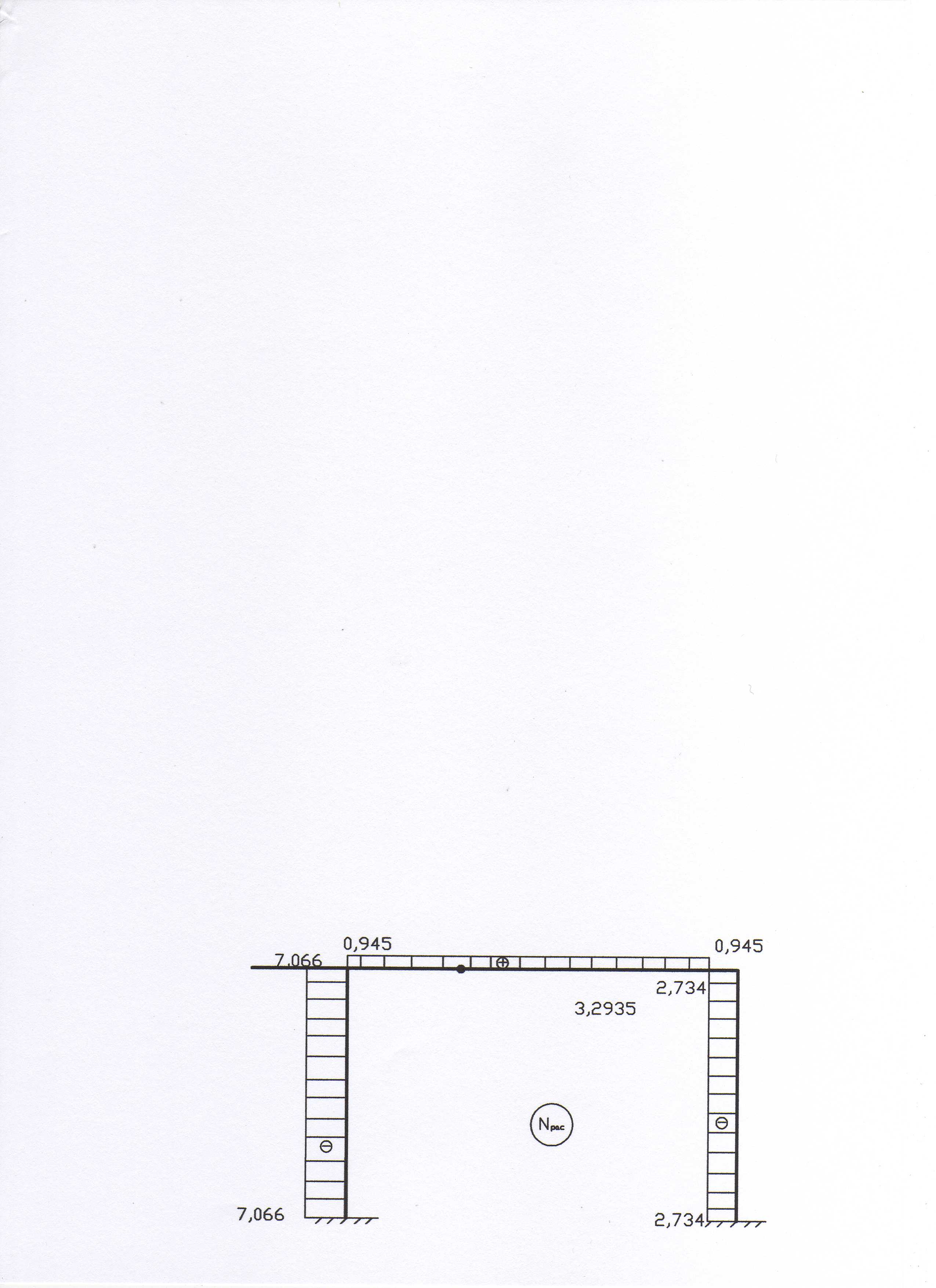
Рис. 20

15. Делаем статическую проверку правильности построения расчетных эпюр. Покажем заданную нагрузку и освободим раму от связей, заметив их реактивными усилиями, взятыми с эпюр , , (рис. 21).

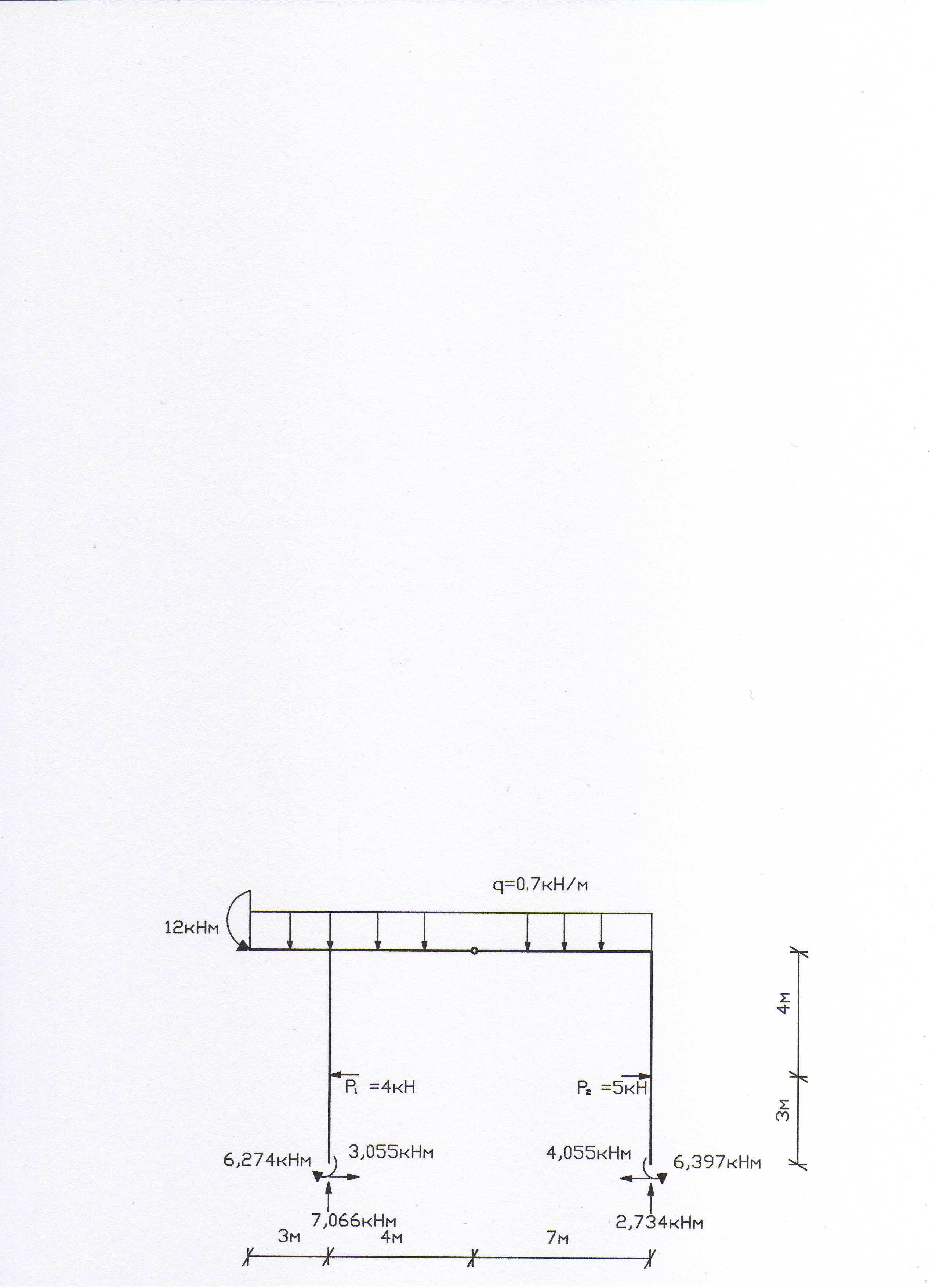
Рис. 21

: -4+5+3.055-4.055=0, 0=0;

: -0.7*14+7.066+2.734=0, 0=0;

: 0.7*14*7+12+4*3-5*3-6.274+6.397-7.066*11=0, 0=0.

Проверка выполнилась. Эпюры построены верно.