Порядок выполнения работы
Определение степени статической неопределимости или числа лишних связей n
Для многоэтажных рам с наличием замкнутых (непрерывных) контуров можно воспользоваться следующей формулой
n
= 3 ( К – 1 ) +
-
Ш , (8)
где К– число замкнутых контуров; – число опорных стержней, Ш–число простых шарниров (которые соединяют два стержня).
Ш =С -1 ,
здесь С – число стержней, соединенных шарниром в одном узле (рис. 1).
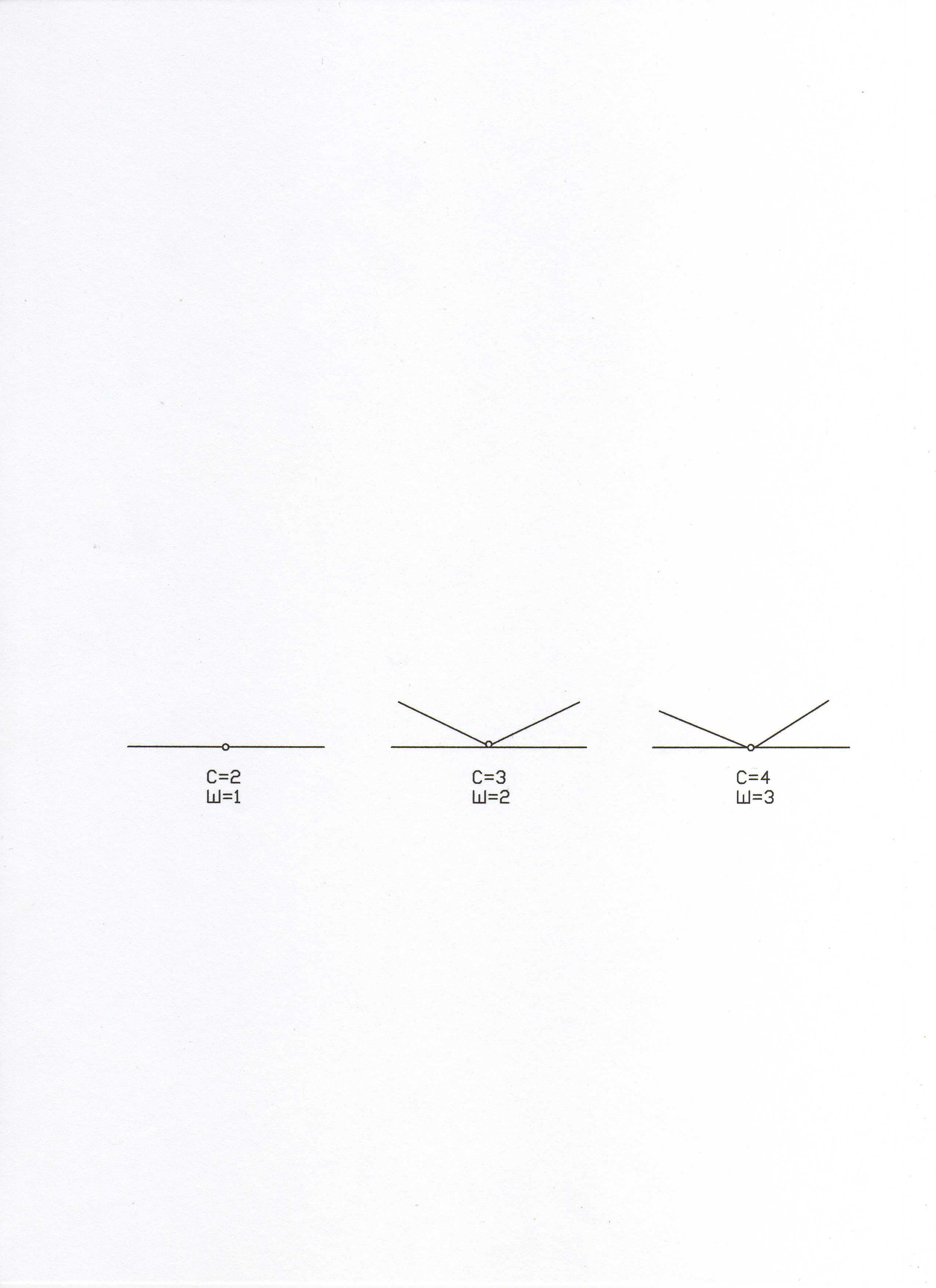
Рис. 1
Для простых рам проще определять степень статической неопределимости по формуле:
n = - 3 – Ш . (9)
На рис. 2 показаны примеры вычисления n по (8) и (9).
а) б)
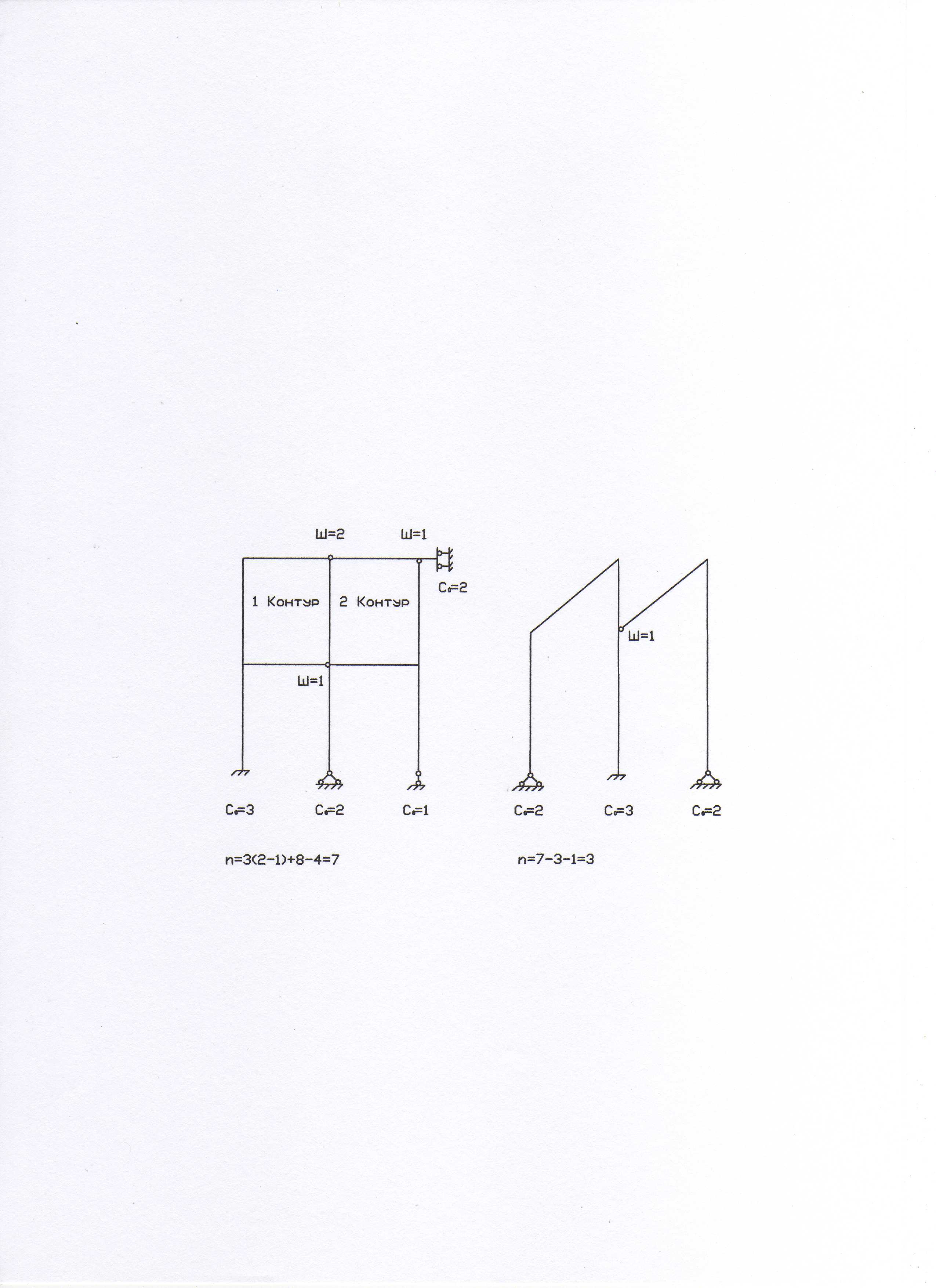
Рис. 2
Выбор основной системы ос
Основная система метода сил получается из заданной путем отбрасывания n лишних связей и заменой их неизвестными реакциями, действующими по направлению отброшенных связей.
ОС должна быть статически определимой и геометрически неизменяемой (т.е. не должна менять свою геометрию без деформаций элементов). Вариантов ОС может быть несколько. Это зависит от выбора отброшенных связей, причем, отбрасываться могут как внешние связи (рис. 3 а), так и внутренние (рис. 3 б, 2 вариант). В работе предлагается выбрать три варианта ОС, а затем принять из них за расчетный наиболее простой для построения эпюр моментов (вариант 1).
а)
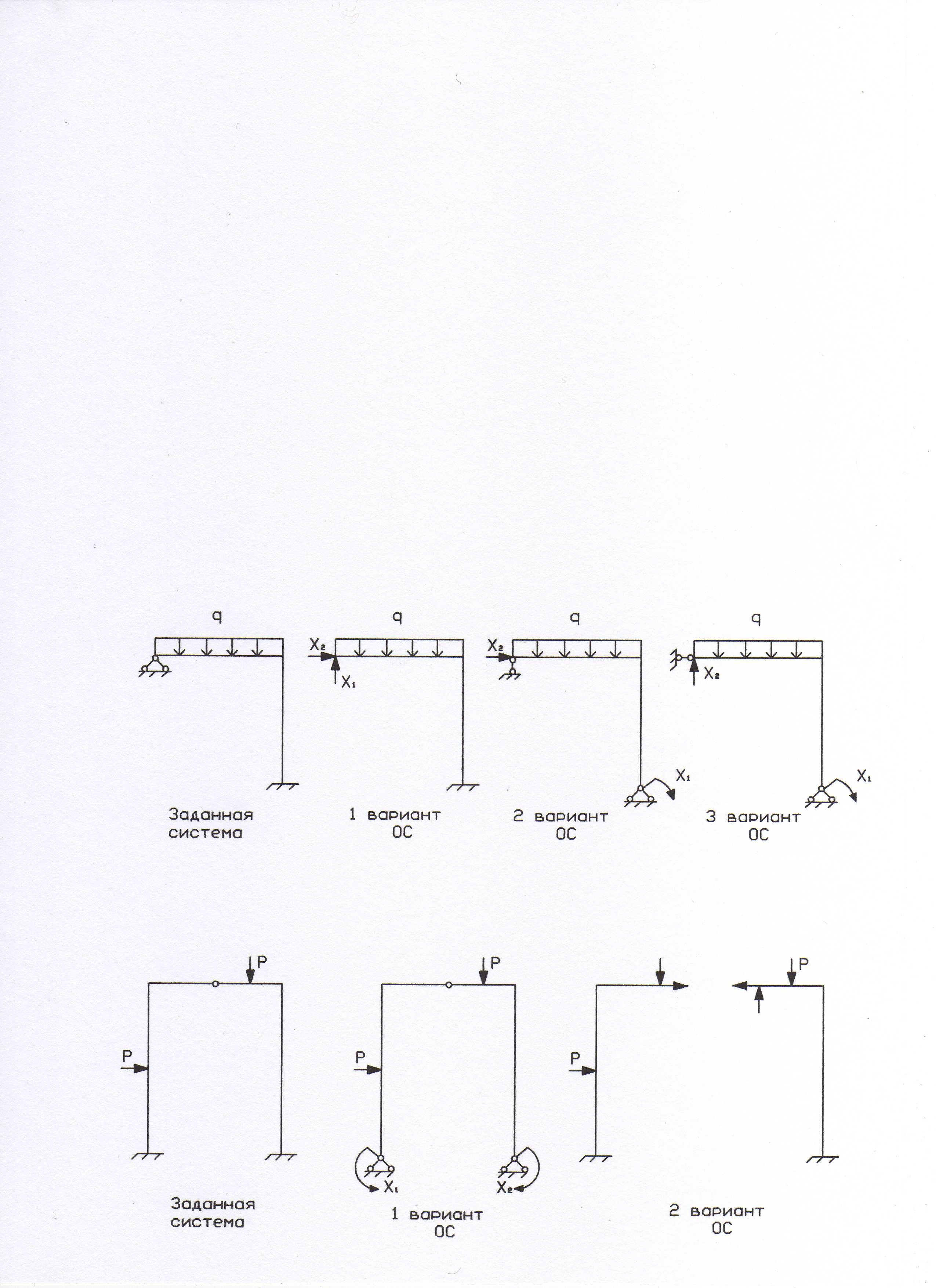
б)
Рис. 3
3. Составление системы канонических уравнений метода сил (ску)
Для определения
неизвестных сил
составляются дополнительные уравнения
совместности деформаций, физический
смысл которых заключается в эквивалентности
перемещений заданной системы и перемещений
в ОС от внешней нагрузки и сил
.
Они записываются в установленной
(канонической) форме вида (1). Число
уравнений системы зависит от степени
статической неопределимости n
.
Для рамы, дважды статически неопределимой, СКУ имеет вид:
4. Построение единичных эпюр моментов
Единичные
эпюры моментов
строятся в ОС от последовательного
приложения сил
= 1,
= 1,
...,
=1
без учета внешней нагрузки по правилам
сопромата для статически определимых
рам. В качестве примера на рис. 4 изображены
эпюры
и
.
Знак на эпюрах моментов не ставится,
они всегда строятся со стороны растянутого
волокна.
Рис. 4
5. Определение главных и побочных коэффициентов ску
Так как по
физическому смыслу
являются
перемещениями, то их можно вычислить
по формуле Мора (2) с помощью формулы
Верещагина, Симпсона, трапеций.
Предварительно единичные эпюры моментов
разбиваются на участки интегрирования
не только по узловым точкам, но и по
точкам изменения характера нагрузки
и точкам изменения
жесткостей EI. Важно правильно применять каждую из формул. Например, формулой Верещагина удобно пользоваться тогда, когда перемножаемые эпюры на участках линейны и имеют вид фигур, для которых легко определить центр тяжести «Ц.Т.» (прямоугольника, треугольника).
По способу Верещагина
=
±
=
±
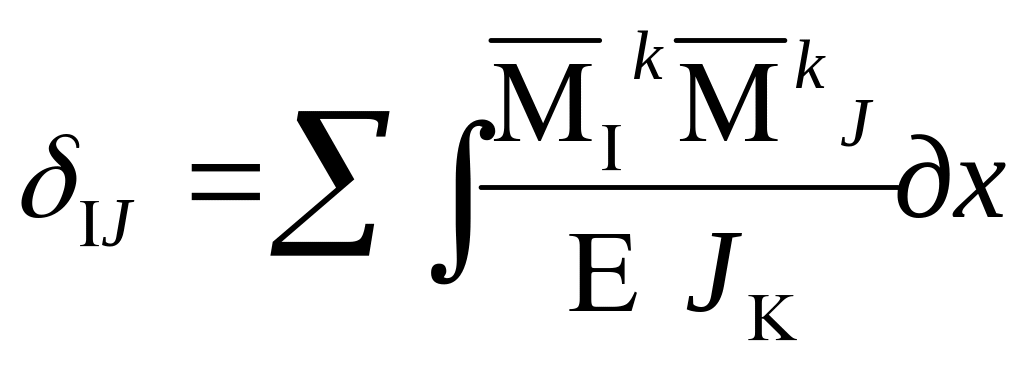, (10)
где
,
– площади эпюры
или
на k–м участке;
,
–ординаты с эпюры
или
под центром тяжести площади эпюры
или
соответственно (таблица ).
Таблица
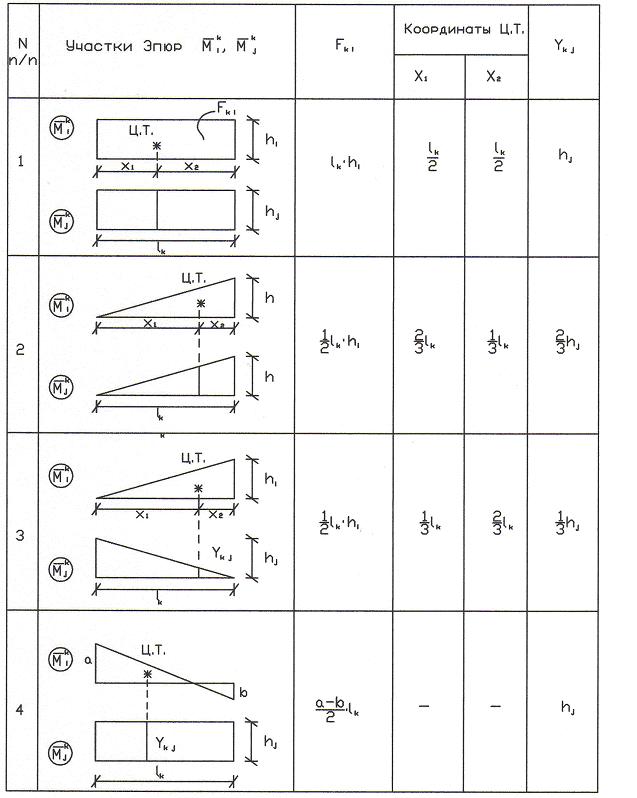
Правило знаков: в формуле (10) ставится знак плюс, когда эпюры и расположены по одну сторону от оси стержня, и знак минус, если по разные.
В качестве примера для рамы, изображенной на рис. 4, вычислим с помощью формулы Верещагина главные коэффициенты СКУ:
=
+
=
;
=
=
.
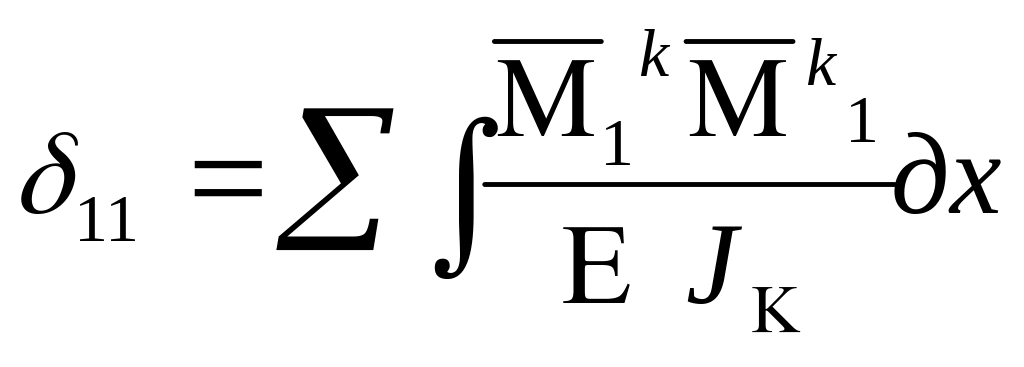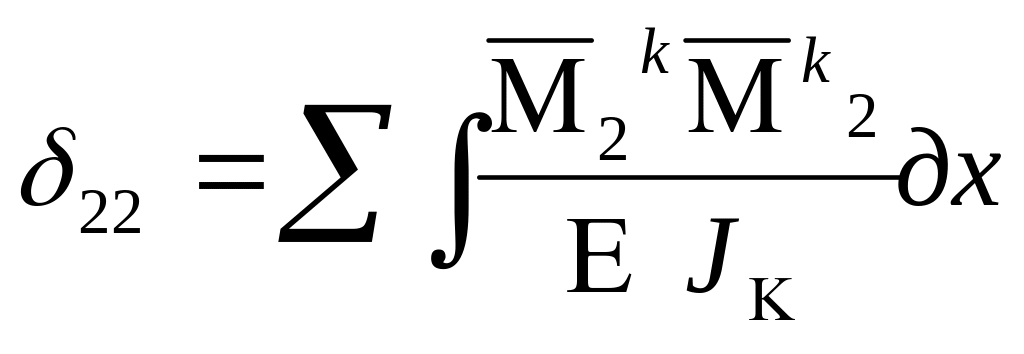По теореме о взаимности перемещений побочные коэффициенты СКУ равны между собой:
=
=
=
.
Формулу Симпсона используют тогда, когда одна из перемножаемых эпюр криволинейна. В этом случае:
=
±
.
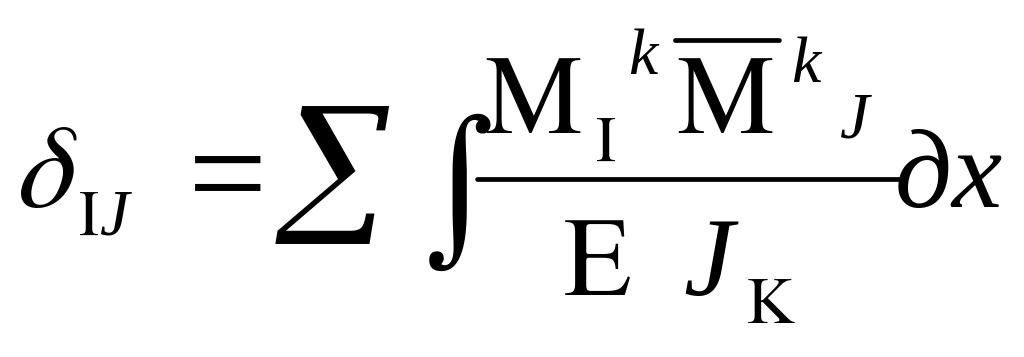(11)
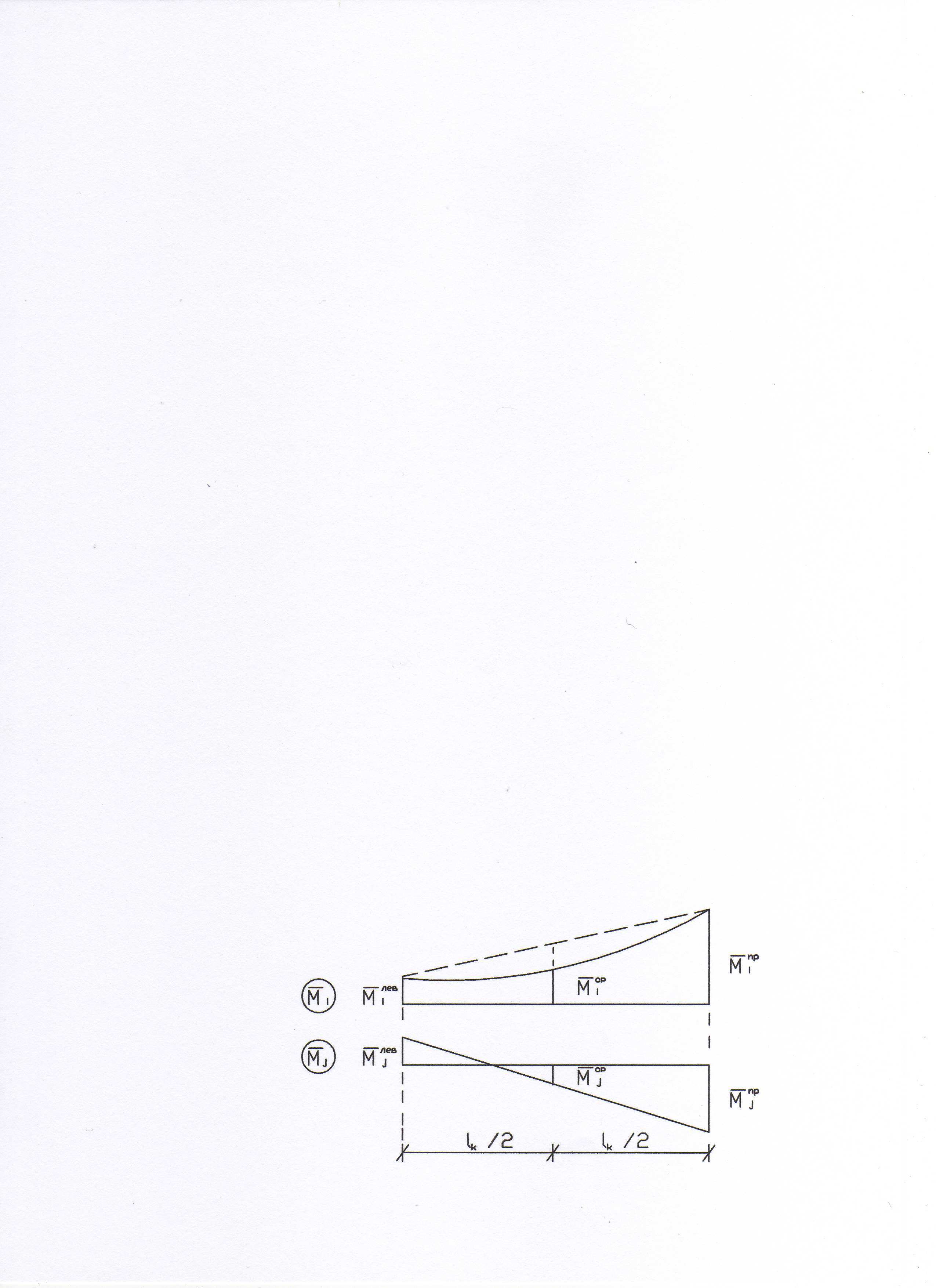
Входящие в формулу величины показаны на рис. 5. Каждое слагаемое в скобках берется со знаком плюс, если соответствующие ординаты расположены по одну сторону от оси, и со знаком минус, если с разных сторон.
.
Рис. 5
Если обе эпюры моментов прямолинейны, то формула Симпсона приводится к формуле трапеций:
=
= ±
.
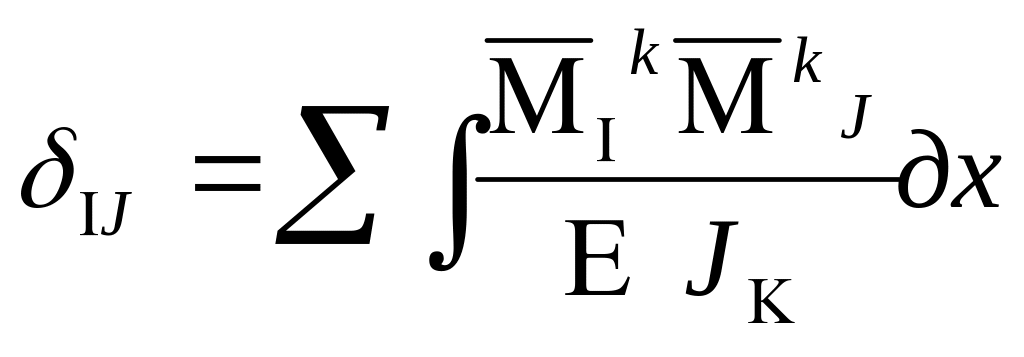(12)
6. Проверка главных и побочных коэффициентов СКУ
Проверка главных и побочных коэффициентов производится с помощью универсального равенства (4). Если оно не выполняется, то для уточнения, в каком перемещении допущена ошибка, делаются построчные проверки каждого канонического уравнения:
.
(13)
1.7. Построение грузовой эпюры моментов
Эпюра
строится в
основной системе от действия только
заданной нагрузки по правилам сопромата
для статически определимых рам. Построим
грузовую эпюру моментов для рамы,
изображенной на рис. 4 (рис. 6).
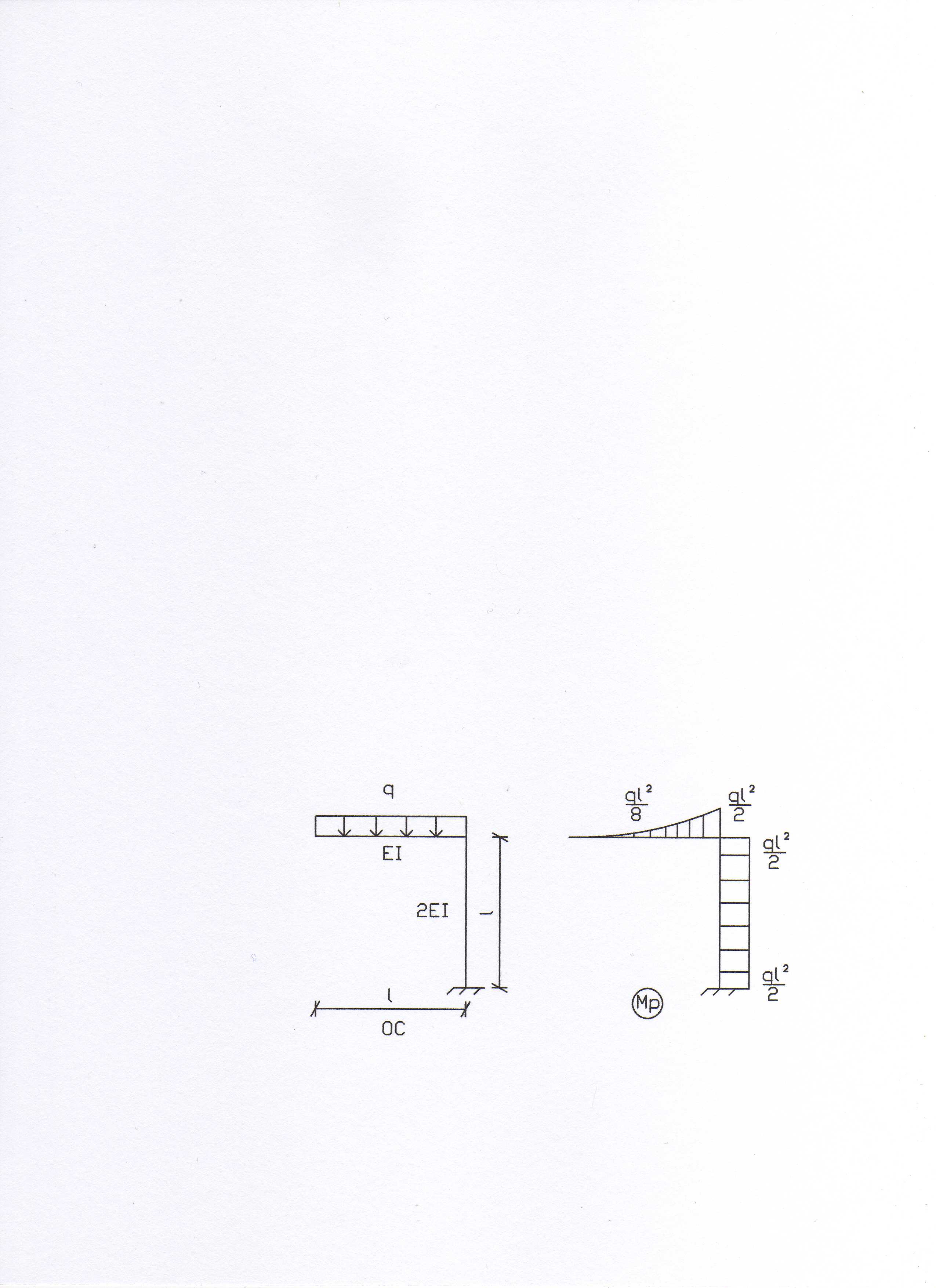
Рис. 6
8. Определение грузовых коэффициентов СКУ
Грузовые коэффициенты определяются также с помощью интеграла Мора по формуле (3):
.
Перемножение единичных эпюр моментов с грузовой делается по формулам Верещагина, Симпсона, трапеций.
9. Проверка грузовых коэффициентов СКУ
Грузовые перемещения проверяются путем перемножения суммарной единичной и грузовой эпюр изгибающих моментов. Полученный результат сравнивается с суммой всех грузовых коэффициентов. В случае правильности вычислений должно выполняться равенство (5):
.
В противном случае следует дополнительно проверить построение грузовой эпюры моментов.
10. Решение системы канонических уравнений
Найденные в п. 5 и п. 8. коэффициенты подставляем в СКУ (1) и решаем ее любым известным способом решения системы линейных алгебраических уравнений. Например, способом Гаусса, способом последовательных приближений, матричным способом и другими.
Определив корни системы уравнений (1), необходимо их проверить подстановкой в исходные уравнения и вычислить погрешность решения, которая не должна превышать 2%.
Погрешность вычислений можно определить по формуле:
,
где П–сумма положительных слагаемых равенства; О–сумма отрицательных слагаемых равенства; М–минимальное число из «П» и «О». Например, погрешность вычисления 42-45-79+80=0 будет равна:
П=42+80=122; О=45+79=124;
М=122;
1.639%.
В результате решения СКУ получаем значения неизвестных усилий в лишних отброшенных связях.