Расчет изгибаемых элементов конструкций
. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ
сечениях стержня (бруса) возникают изгибающие моменты.
Если изгибающий момент в сечении является единственным силовым фактором, а поперечные и нормальные силы отсутствуют, изгиб называется
чистым.
Если наряду с этим действуют и поперечные силы, изгиб поперечным. Когда в сечениях возникают несколько силовых факторов – сложный
изгиб.
Расчеты бруса основываются на принципе независимости действия сил.
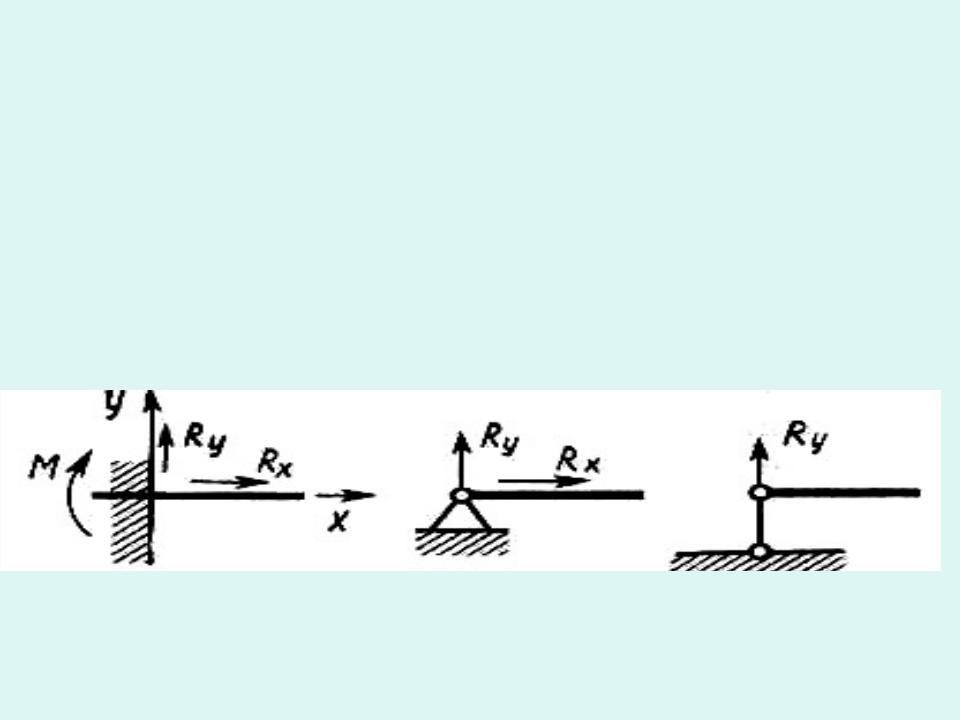
Опоры и опорные реакции.
Различают три основных типа опор
|
шарнирно- |
шарнирно- |
|
|
подвижная |
||
Жесткое защемление |
неподвижная опора |
||
опора , передает |
|||
(заделка), |
допускает лишь угловое |
||
нагрузки лишь в |
|||
исключающее осевые и |
смещение (поворот |
||
угловые смещения |
вокруг собственной оси) |
направлении |
|
этой оси. |
|||
|
|
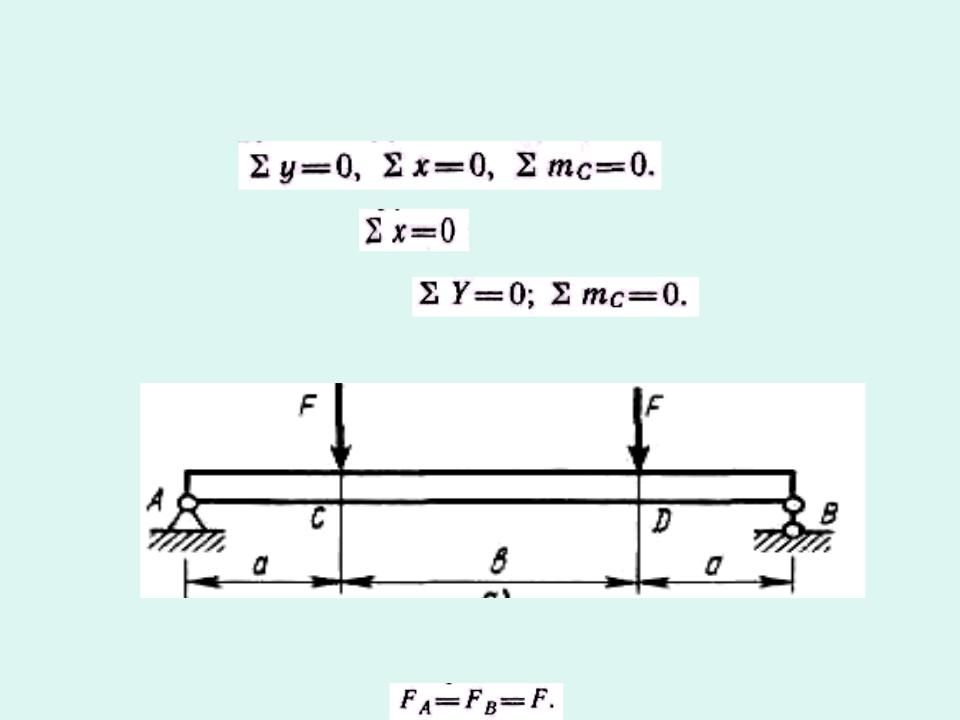
Горизонтальный стержень на опорах, испытывающий деформации изгиба, называют балкой.
В местах закрепления возникают опорные реакции. Их находят из уравнений статики. Условия равновесия стержня при действии на него плоской системы сил :
Если нагрузка по оси стержня |
то опорные реакции |
определяются по двум уравнениям
Внутренние силовые факторы.
Из условия равновесия найдем опорные реакции
Для определения внутренних силовых факторов стержня на участка CD разрежем его на две части и рассмотрим равновесие одной из них.
Для чего, приложим в точке |
при |
неизвестные внутренние силовые факторы:
нормальную силу перерезывающую силу
изгибающий момент
Составим уравнения равновесия:
∑
Учитывая, что , из этих уравнений
найдем:
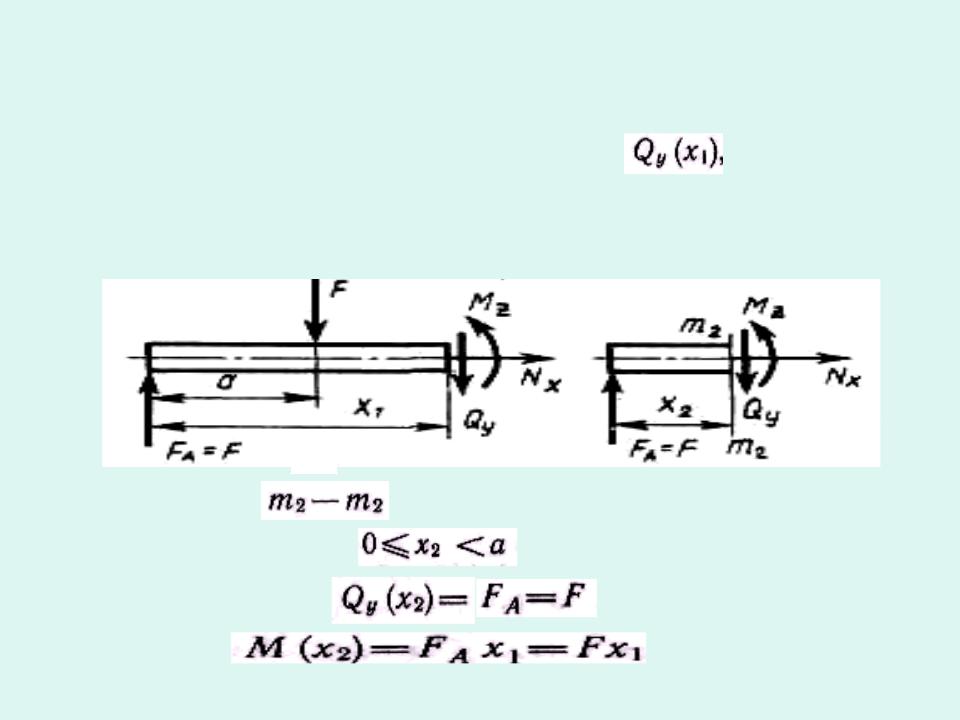
Изгибающий момент действующий в сечении стержня равен сумме моментов внешних сил, действующих на отсеченную часть,
M Z (X) = ∑m i
.В рассмотренном примере перерезывающая |
= 0 |
|
сила |
||
|
Стержень на участке CD находится в состоянии чистого изгиба. Такой же результат будет получен из рассмотрения равновесия правой части стержня.
Если взять |
на участке АС и рассмотреть равновесие |
сечение |
|
левой части, то при |
|
Следовательно, этот участок стержня находится в условиях поперечного изгиба.
Построение эпюр.
Эпюры - графики изменений поперечных сил и изгибающих моментов вдоль центральной оси стержня.
•Определить опорные реакции.
•Разбить стержень на участки с однородной внешней нагрузкой.
•Рассмотреть произвольное сечение в пределах данного участка и составить
общие выражения для поперечной силы и изгибающего момента .
•Выбирая произвольные значения в пределах этого участка, находим ординаты эпюр.
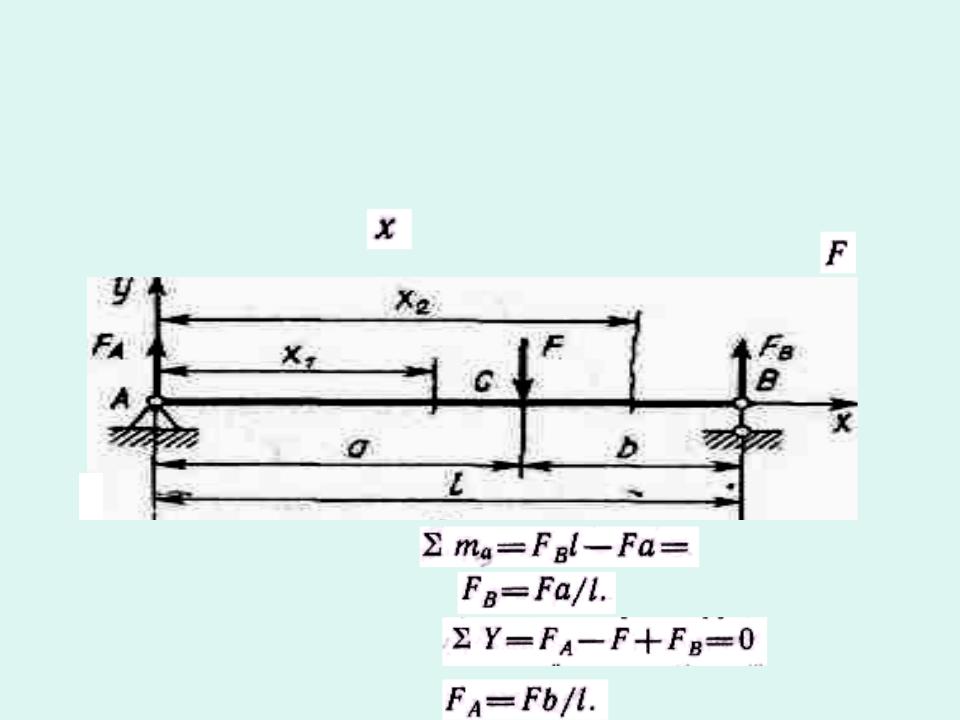
Рассмотрим двухопорный стержень, нагруженный сосредоточенной си
Из уравнения |
О |
равновесия |
|
находим реакцию в правой опоре |
|
Из второго уравнения равновесия
находим реакцию в левой
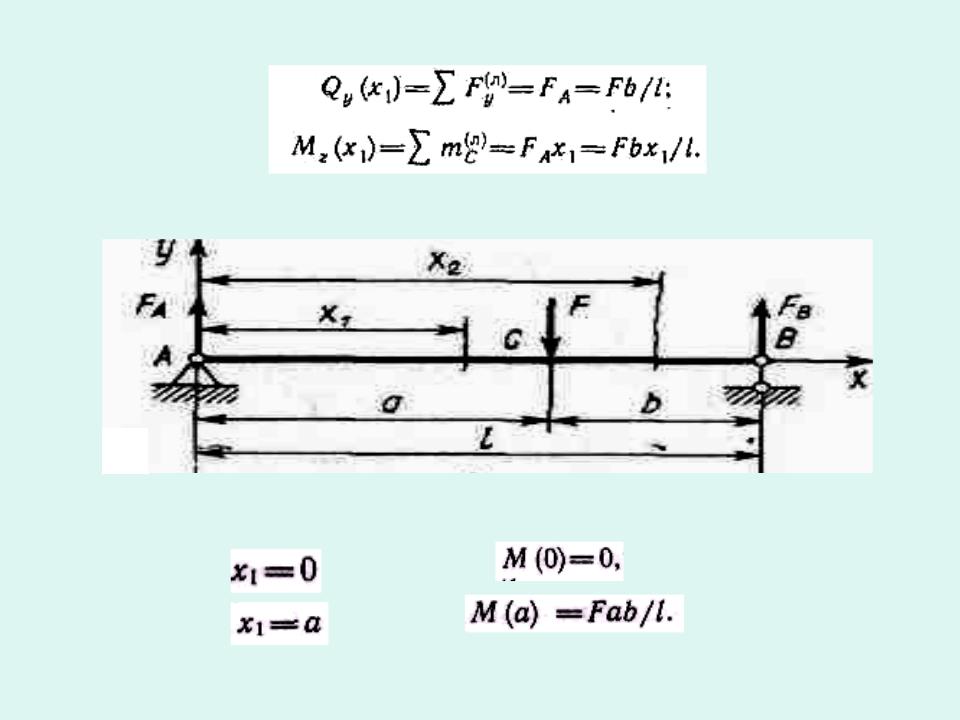
Рассматриваемый стержень содержит два участка (АС и CD) с однородной нагрузкой. Составим (с учетом правила знаков) уравнения равновесия для первого участка
В этих уравнениях перерезывающая сила на участке АС положительна и постоянна
Изгибающий момент линейно зависит от абсциссы 
сечения при момент
при момент
На втором участке |
при |
эти уравнения примут |
|
СВ |
вид: |
||
|
Эпюры
перерезывающих
сил и изгибающих
моментов
Перерезывающая сила на этом участке отрицательная и постоянна. Изгибающий
момент изменяется |
линейно, |
|
|
при |
момент |
|
|
и при |
= ℓ |
момент М ( b ) = 0 |
( ℓ – a = b) |
Эпюра перерезывающих сил в точке приложения сосредоточенной
имеет скачок на величину этой силы, а эпюра изгибающего момента имеет излом
ЧИСТЫЙ ИЗГИБ
НАПРЯЖЕНИЯ В СТЕРЖНЕ ПРИ ЧИСТОМ ИЗГИБЕ
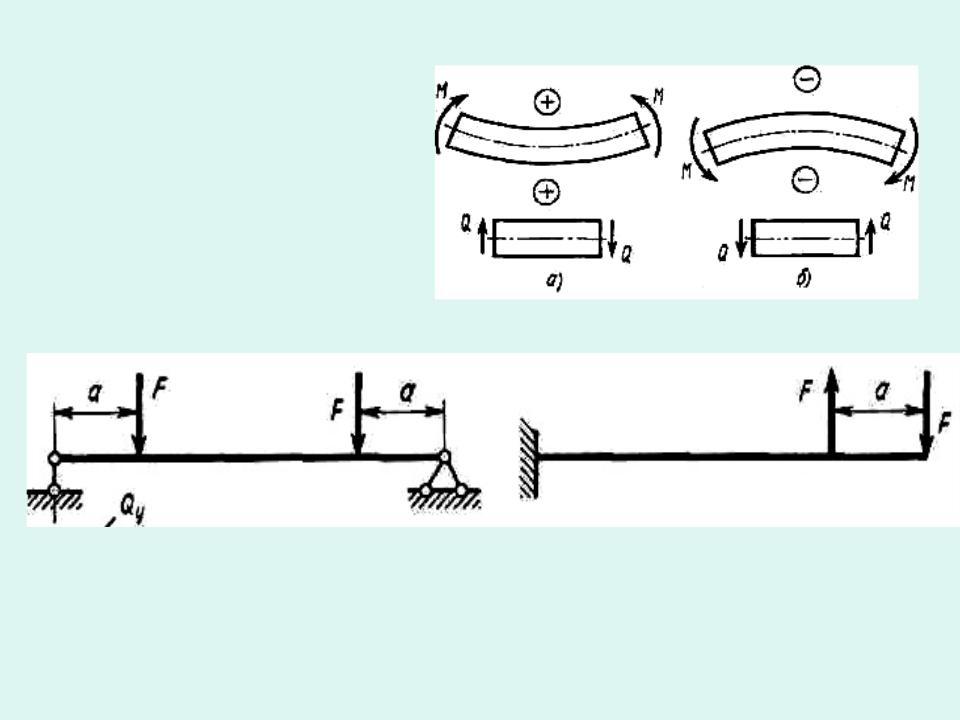
Чистый изгиб - в поперечных сечениях стержня действует только изгибающий момент а перерезывающая сила отсутствует.
В соответствии с характером деформаций стержня примем
следующие
правила знаков
согласно рисунка.
Напряжения в поперечном сечении стержня при чистом изгибе .
Чистый изгиб стержня характеризуется тем, что его волокна на выпуклой стороне растягиваются, а на вогнутой стороне — сжимаются. Существует нейтральный слой. и нейтральная линия (н. л.).