Лекція

Розділ 1. Лінійна алгебра

Тема: Матриці. Дії з ними.

1. Матриці, види матриць.

2. Дії над матрицями.

Означення. Матрицею розміром n×m називається прямокутна таблиця чисел

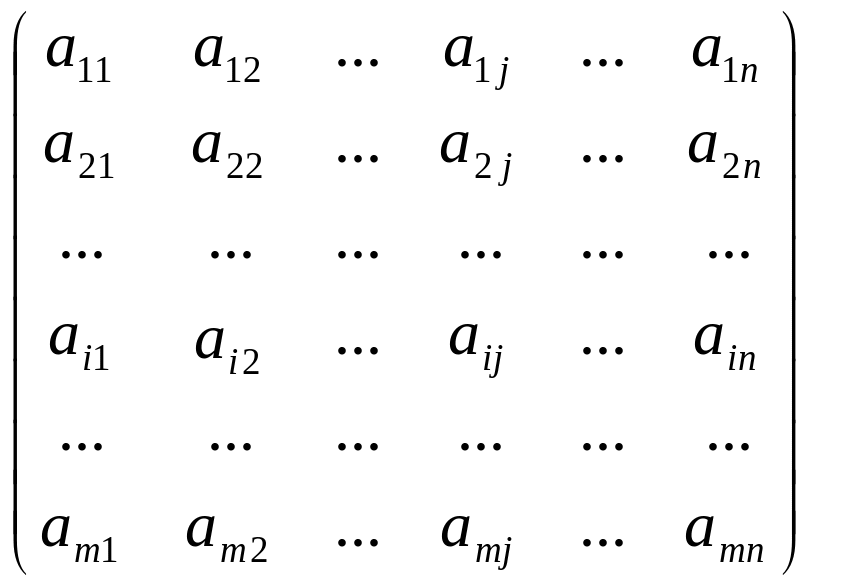
де наз. елементами матриці.

Види матриць:

1. Матриця називається квадратною, якщо кількість її рядків співпадає із кількістю стовпців (n=m).

2. Матриця O називається нульовою, якщо всі її елементи є нулями: .

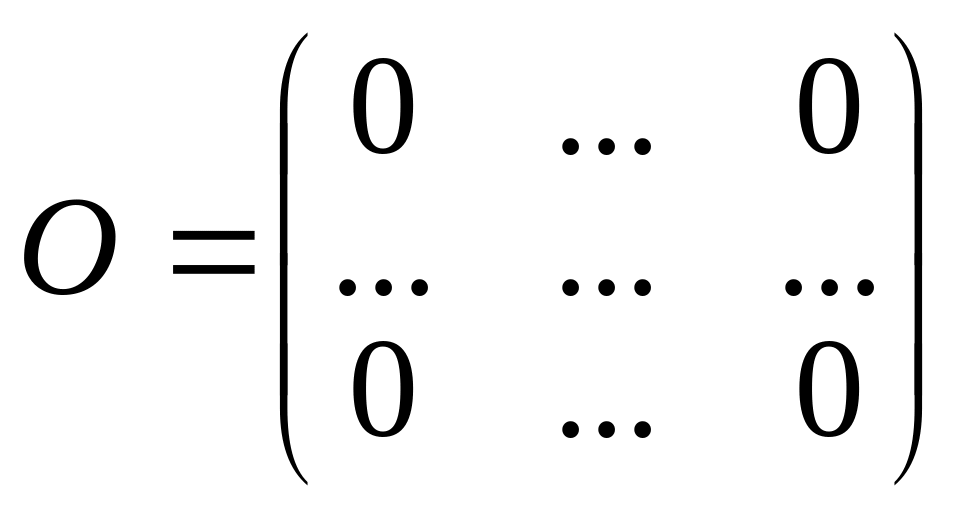3. Частковим випадком матриці є вектор (упорядкована послідовність чисел). Розрізняють вектор-рядок (матрицю-рядок) 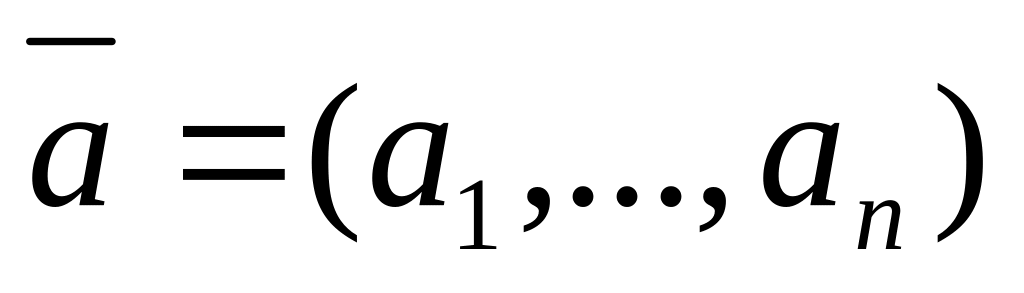та вектор-стовпець (матрицю-стовпець) .

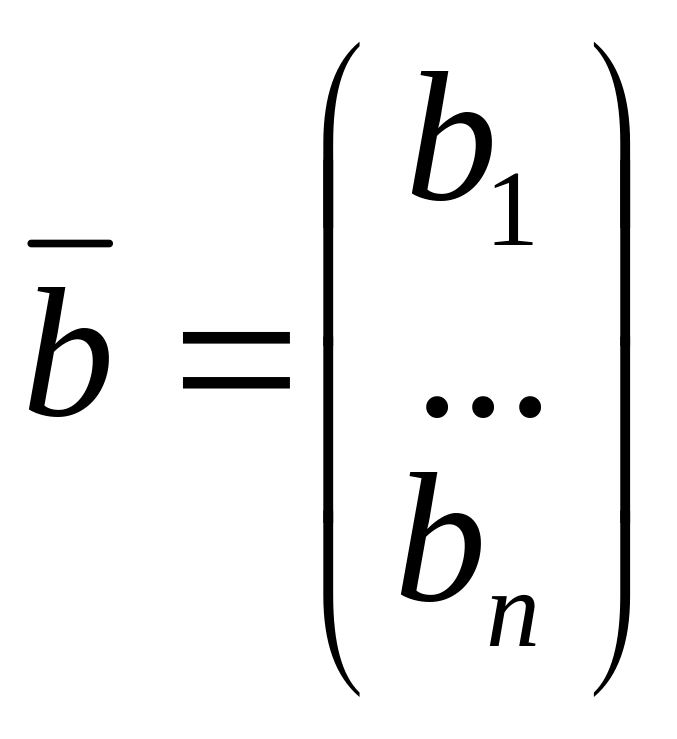Нехай задані матриці

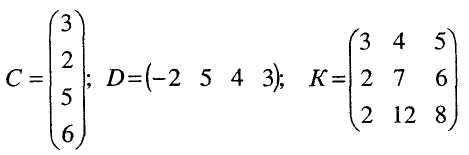
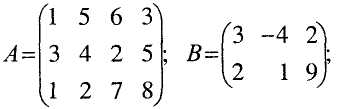
Матриця А має розмір 34, матриця В розміру 23, матриця-стовпець С розміру 41, D – матриця-рядок розміру 14, матриця К - квадратна порядку 3.

Елементи квадратної матриці А порядку n, що розташовані на діагоналі матриці, яка проходить з лівого верхнього кута до правого нижнього кута, утворюють головну діагональ матриці.

Елементи квадратної матриці, що розташовані на діагоналі матриці, яка проходить з правого верхнього кута до лівого нижнього кута, утворюють неголовну (допоміжну) діагональ матриці.

Наприклад, в матриці К елементами головної діагоналі будуть 3, 7, 8, а допоміжної – 5, 7, 2

4. Квадратна матриця зветься діагональною, якщо усі її елементи дорівнюють 0, крім елементів головної діагоналі.

5. Діагональна матриця, усі елементи якої дорівнюють одинці, називається одиничною матрицею і позначається Е, тобто ця матриця має вигляд

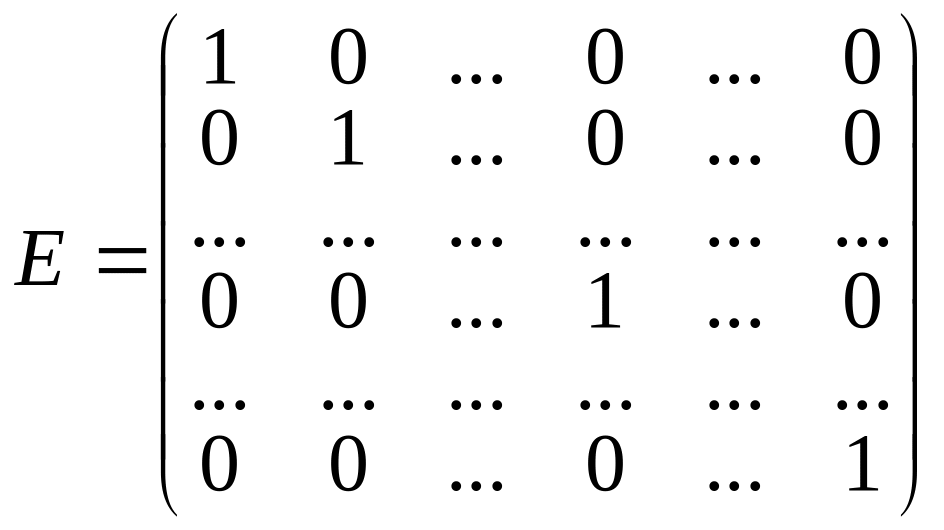
6. Квадратна матриця називається трикутною, якщо всі її елементи, розміщені під головною діагоналлю або над нею, дорівнюють нулю.

Розглянемо дві матриці

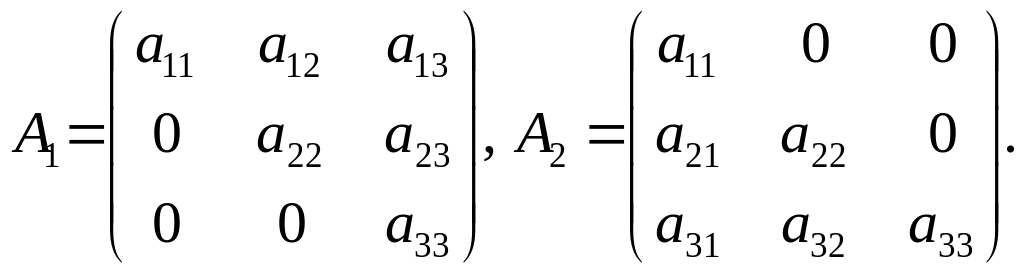
Матриця А₁ називається верхньою трикутною, а матриця А₂ — нижньою трикутною.

Дії над матрицями:

1. Матриці A=(a_ij) та B=(b_ij) називаються рівними (однаковими), якщо вони мають однакову кількість рядків та стовпців і всі їхні елементи, розташовані на однакових місцях, є рівними (тобто a_ij=b_ij для всіх значень i та j).

2. Сумою двох матриць A=(a_ij) та B=(b_ij) з однаковою кількістю рядків та стовпців називається матриця C=A+B, де

c_ij=a_ij+b_ij (i=1,…,m; j=1,…,n).

Приклад

Нехай та .

Тоді

3. Добутком матриці A=(a_ij) на число k називається матриця, елементи якої дорівнюють добуткам відповідних елементів матриці А та числа к:

Приклад

Нехай .

,

4. Добуток АВ матриць А та В існує лише при виконанні умов узгодженості: кількість стовпців матриці А (першого множника) дорівнює кількості рядків матриці В (другого множника).

Добутком АВ матриці А розміру mn матриці В розміру пр називається матриця С розміру mр, елементи якої c_ij дорівнюють сумі добутків елементів і-го рядка матриці А на відповідні елементи j-ro стовпця матриці В.

Таким чином, кожен елемент матриці С знаходиться за формулою:

Приклади.

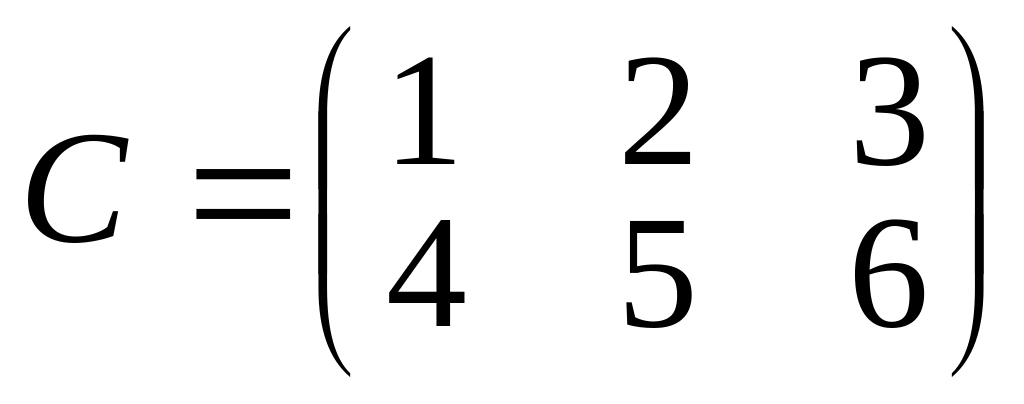1. та .

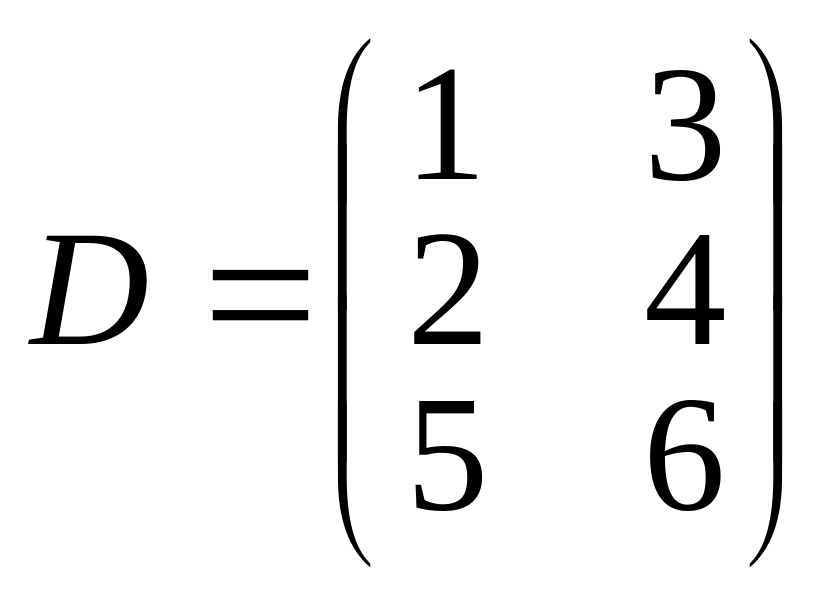Тоді ,

DC - не має сенсу,

2. Нехай та .

Зазначимо, що в останньому прикладі АВ  ВА .

Взагалі добуток матриць не має властивості комутативності, тобто АВ#ВА. Якщо добуток двох матриць не залежить від порядку множників, тобто АВ=ВА, тоді кажуть, що ці матриці комутують.

Наприклад, якщо А - квадратна матриця порядку n, E -одинична матриця порядку п, тоді АЕ = ЕА = А.

Означення. Якщо в матриці А рядки записати стовпцями із збереженням їх нумерації, то одержана матриця зветься транспонованою і позначається А^т, а вказана операція перетворення матриці А називається транспонуванням матриці А.

 

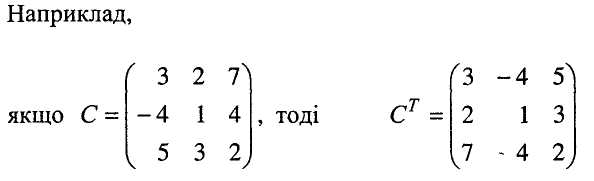
Приклад. Для виготовлення виробів W1 та W2 потрібні вузли v1 та v2. Для виготовлення цих вузлів, в свою чергу, відповідно, потрібні деталі d1, d2 та d3 у кількостях, що наведені у таблицях:

Вироби	Кількість вузлів			Вузли	Кількість деталей
	v1	v2			d1	d2	d3
W1	2	3		v1	2	1	0
W2	1	4		v2	1	0	3

Обчислити кількість деталей, що потрібні для виготовлення кожного із виробів W1 та W2.

На основі аналізу цих таблиць бачимо, що шукана кількість деталей облислюється як добуток матриць

.

Отриманий результат такий:

Вироби	Кількість деталей
	d1	d2	d3
W1	7	2	9
W2	6	1	12

Зокрема, для виготовлення виробу W2 потрібно 12 деталей d3.

Приклад. Нарахувати заробітну плату, яку потрібно виплатити на кожне замовлення, якщо вхідна інформація задана у таблицях:

Таблиця A

Виріб	Затрати робочого часу на робочих місцях, год.
	1	2	3	4
W1	0,8	2,1	1,2	3,0
W2	1,3	0,5	2,8	0,2
W3	1,1	1,0	2,5	1,8

Таблиця B

Замовлення	Кількість виробів
	W1	W2	W3
Z1	5	7	3
Z2	4	0	2
Z3	6	2	1

Таблиця C

Робоче місце	Погодинна заробітна плата, грн.
1	1,30
2	1,25
3	1,40
4	1.45

Помноживши матрицю B на матрицю A, отримуємо затрати часу на робочих місцях щодо кожного замовлення:

Замовлення	Затрати робочого часу на робочих місцях, год.
	1	2	3	4
Z1	16,4	17	33,1	21,8
Z2	5,4	10,4	9,8	15,6
Z3	8,5	14,6	15,3	20,2

Справді, .

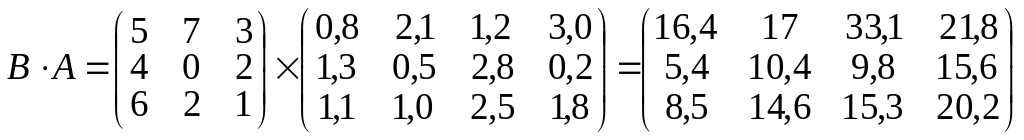Перемноживши отриману матрицю на вектор (матрицю-стовпець) C, обчислимо витрати на зарплату щодо кожного із замовлень:

Замовлення	Витрати на зарплату
Z1	120,52
Z2	56,36
Z3	80,01

Отже, витрати на зарплату обчислюються як добуток матриць:

.
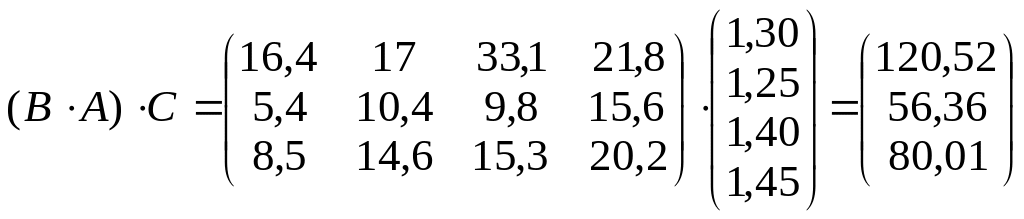