ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Орловский государственный технический Университет

Д.Н. Ешуткин и др.

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНЫХ РАБОТ

Задание С-3. Пространственная система сил

Рекомендовано редакционно-издательским советом ОрелГТУ

в качестве учебного пособия

Орел 2006

УДК Е 96 531 (076)

ББК 22.21 7

Е 96

Рецензенты:

кандидат технических наук, заведующий кафедрой общеинженерных дисциплин Орловского государственного аграрного университета

Г.М. Абрамов,

кандидат технических наук, доцент кафедры «Динамика и прочность машин»

А.Ю. Корнеев

Е 96 Ешуткин, Д.Н. Теоретическая механика, задания для самостоятельных работ: учебное пособие/ Д.Н. Ешуткин, А.И. Пономарев, Е.Н. Грядунова, А.В. Журавлева. — Орел: ОрелГТУ, 2006. — 122 с.

Учебное пособие содержит задания для самостоятельных работ, которые охватывают все основные разделы теоретической механики: статику, кинематику и динамику, и задачи по всем главным темам этих разделов. К каждому заданию дается подробное указание по выполнению, формулы и примеры.

Учебное пособие отвечает содержанию рабочих программ по теоретической механике и предназначено студентам, обучающимся на всех специальностях очной и заочной форм обучения, изучающих дисциплину «Теоретическая механика».

УДК 531 (076)

ББК 22.21 7

Е 96

© ОрелГТУ, 2006

ВВЕДЕНИЕ

Теоретическая механика – это наука о законах механического движения и равновесия материальных тел. Под механическим движением понимается изменение относительного положения материальных тел в пространстве с течением времени. Теоретическая механика изучает наиболее общие законы механического движения. Она не учитывает индивидуальные свойства материальных тел, за исключением двух свойств: протяженности и гравитации. Наблюдать и изучать механическое движение материальных тел можно по отношению к другим материальным телам, принятым за тела отсчета. С этими телами обычно связывают систему координатных осей, которую называют системой отсчета. Частным случаем механического движения является равновесие материальных тел.

Теоретическую механику условно делят на статику, кинематику и динамику.

В данном пособии приведены достаточно простые задачи по основным разделам теоретической механики, решение которых позволяет освоить основные алгоритмы применения теоретических положений на практике.

Характерная особенность приведенных заданий – несложность использования математических выкладок и их физическая прозрачность, что позволяет не акцентировать внимание студента на конкретных условиях задачи, а понять при самостоятельной работе алгоритм решения подобного класса задач.

1 СТАТИКА

Статикой называют раздел теоретической механики, в котором изучаются методы преобразования системы сил, а также ставятся условия их равновесия.

1.3 Задание С-3. Пространственная система сил

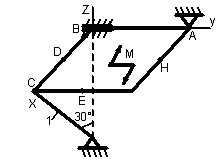
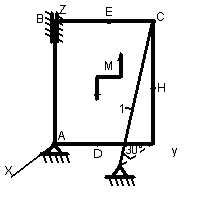
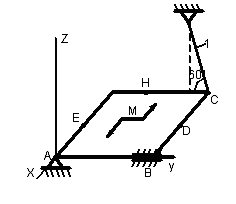
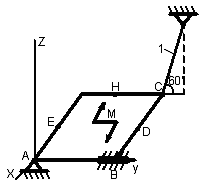
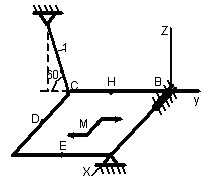
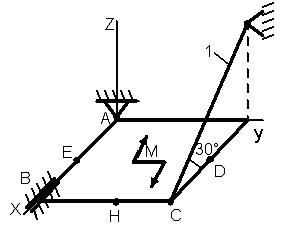
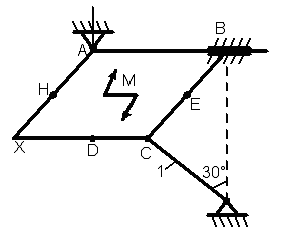
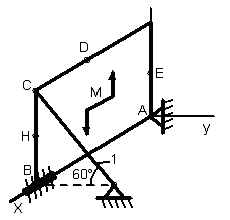
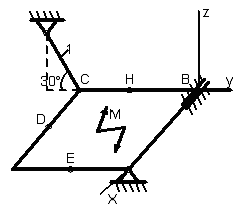
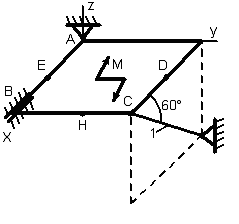
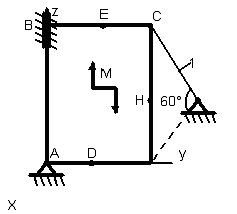
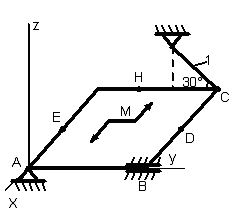
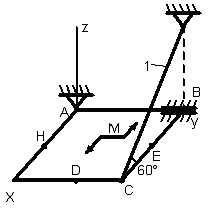
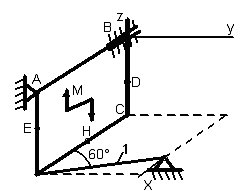
1.3.1 Определение реакций связей твердого тела

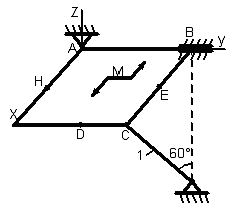
Однородная тонкая прямоугольная плита весом Р = 10 кН со сторонами АВ = 3L и ВС = 2L закреплена в точке А сферическим шарниром, а в точке В цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем 1, закреплённым на концах шарнирно (рис. 1.65–1.94). На плиту действуют пара сил, лежащая в плоскости плиты, с моментом кН∙м, и две силы. Значения, направления и точки приложения сил и моментов указаны в табл. 3; при этом силы и лежат в плоскостях, параллельных плоскости , сила - в плоскости, параллельной , а сила - в плоскости, параллельной . Точки приложения сил (D, Е, Н) находятся в середине соответствующих плит. Определить реакции связей в точках А и В и реакцию стержня. При подсчётах принять L = 0,6 м.

1.3.2 Указания по выполнению задания С-3

При решении данной задачи следует учесть, что реакция цилиндрического шарнира (подшипника) разлагается на две составляющие, лежащие в плоскости перпендикулярно к оси шарнира, а реакция сферического шарнира разлагается на три составляющие. При вычислении моментов сил относительно координатных осей в некоторых случаях удобно разложить силы на составляющие, параллельные координатным осям, и воспользоваться теоремой Вариньона:

где =.

Таблица 3

Данные к заданию С-3

Вариант
	точка приложения	α1, град	точка приложения	α2, град	точка приложения	α3, град	точка приложения	α4, град
1	2	3	4	5	6	7	8	9
1	-	-	E	90	D	30	-	-
2	-	-	-	-	D	0	E	60
3	-	-	H	30	-	-	D	90
4	-	-	D	60	H	0	-	-
5	E	0	-	-	H	60	-	-
6	-	-	-	-	E	30	H	0
7	-	-	E	60	-	-	D	90
8	H	90	D	30	-	-	-	-
10	D	60	-	-	E	0	-	-

Рис. 1.65	Рис. 1.66
Рис. 1.67	Рис. 1.68
Рис. 1.69	Рис. 1.70
Рис. 1.71	Рис. 1.72
Рис. 1.73	Рис. 1.74
Рис. 1.75	Рис. 1.76
Рис. 1.77	Рис. 1.78
Рис. 1.79	Рис. 1.80
Рис. 1.81	Рис. 1.82
Рис. 1.83	Рис. 1.84
Рис. 1.85	Рис. 1.86
Рис. 1.87	Рис. 1.88
Рис. 1.89	Рис. 1.90
Рис. 1.91	Рис. 1.92
Рис. 1.93	Рис. 1.94

1.3.3 Примеры выполнения задания С-3

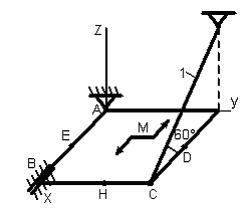
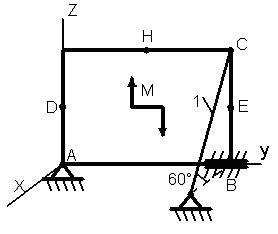
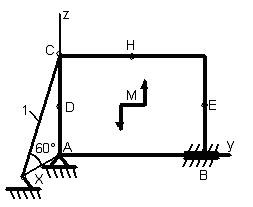
Пример С-1.3. Однородная прямоугольная плита весом Р = 6 кН со сторонами АВ = 3L и ВС = 2L закреплена в точке В цилиндрическим шарниром и удерживается в равновесии стержнем 1, закреплённым на концах шарнирами .

На плиту действует пара сил, лежащая в плоскости плиты, с моментом М = 8 кН∙м и три силы, приложенные в точках Н, D и Е. Причём , сила лежит в плоскости хz, параллельна оси Оz, а лежит в плоскости ху. Углы между силами и соответствующими линиями указаны на рис. 1.95. Точки Н, D, Е находятся в середине соответствующей плиты. Определить реакции в точках А и В и реакцию стержня. При подсчётах принять L = 0,4 м(рис. 1.95).

Решение:

Рассмотрим равновесие плиты. На неё действуют силы и пара сил с моментом М, три составляющие реакции сферического шарниpа, две составляющие Х_В, Y_В реакции подшипника, реакцию стержня N направляем вдоль стержня.

Для определения шести неизвестных реакций составим шесть уравнений равновесия произвольной пространственной системы сил. Для расчета моментов сил и относительно осей разлагаем эти силы на составляющие и применим теорему Вариньона:

,

где

.

Уравнения равновесия:

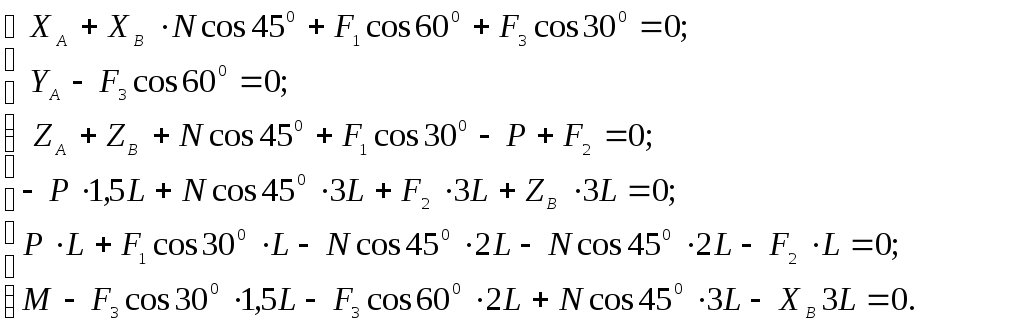(1.1)

Из пятого уравнения системы (1.1) находим:

Из шестого уравнения системы (1.1) получим:

Из четвертого уравнения системы (1.1) имеем:

.

Из третьего уравнения системы (1.1) получаем:

Из второго уравнения системы (1.1) находим:

кН.

Из первого уравнения системы (1.1) имеем:

.

кН.

Ответ: кН; кН; кН; кН; кН.

Знак «минус» указывает, что силы направлены противоположно показанным на рис. 1.95.

Приложения А

Образец оформления титульного Титульный листа

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Орловский государственный технический Университет

Кафедра - "Теоретическая и прикладная механика"

Расчетно-графическая работа

по дисциплине "Теоретическая механика"

Название работы

Работу выполнил студент

Группа

Специальность

Вариант

Руководитель

Орел, 200 г.

Литература

1. Тарг, С.М. Краткий курс теоретической механики/ С.М. Тарг. - М.: Наука, 1972. – 478 с.

2. Яблонский, А.А. Курс теоретической механики. Часть 1, 2/ А.А. Яблонский, В.М. Никифорова. - М.: Высш. школа, 1984. – 343 с.

3. Добронравов, В.В. Курс теоретической механики/ В.В. Добронравов, Н.Н. Никитин, А.Л. Дворников. - М.: Высш. школа 1983. – 575 с.

4. Воронков, И.М. Курс теоретической механики/ И.М. Воронков. - М.: Наука, 1966. – 596 с.

5. Савин, Г.Н. Курс теоретической механики/ Г.Н. Савин, Т.В. Путята, Б.Н. Фрадлин. - Киев: Высш. школа, 1973. – 359 с.

6. Лойцянский, Л.Г. Курс теоретической механики. Т.1./ Л.Г. Лойцянский, А.И. Лурье. - М.: Наука, 1982. – 352 с.

7. Бать, М.И. Теоретическая механика в примерах и задачах. Часть 1./ М.И. Бать, Г.Ю. Джанелидзе, А.С. Кельзон. - М.: Наука, 1984. – 503 с.

8. Ешуткин, Д.Н. Сборник задач по теоретической механике/ Д.Н. Ешуткин, А.И. Пономарев, Е.Н. Грядунова. – Орел: ОрелГТУ, 2005. – 88с.