
- •III осенний семестр Лекция №1 Числовые ряды
- •Лекция №2 Сходимость положительных рядов
- •Лекция №3 Сходимость положительных рядов (продолжение)
- •Лекция №4 Сходимость положительных рядов (продолжение)
- •Ряды с членами произвольного знака
- •Лекция №5 Ряды вида
- •Лекция №6 Перестановки числовых рядов
- •Лекция №6 Перестановки числовых рядов (продолжение)
- •Лекция №8 Умножение рядов (продолжение)
- •Двойные ряды
- •Лекция №9 Двойные ряды (продолжение)
- •Бесконечные произведения
- •Лекция №10 Бесконечные произведения (продолжение)
- •Лекция №11 Функции, представляющиеся в виде бесконечных произведений
- •Функциональные последовательности и ряды
- •Лекция №12 Функциональные последовательности и ряды (продолжение)
- •Лекция №13 Функциональные последовательности и ряды (продолжение)
- •Лекция №14 Свойства предельной функции и сумма функционального ряда в случае равномерной сходимости
- •Лекция №15 Пространства и сходимость в них
- •Степенные ряды
- •Лекция №16 Степенные ряды (продолжение)
- •Лекция №17 Разложение функций в степенные ряды
- •Лекция №18 Ряды Фурье
- •Лекция №19 Ряды Фурье (продолжение)
- •Лекция №20-21 Ряды Фурье (продолжение)
- •Лекция №22 Ряды Фурье (продолжение)
- •Лекция №23 Ряды Фурье (продолжение)
- •Лекция №24 Ряды Фурье (продолжение)
- •Лекция №25 Ряды Фурье (продолжение).
- •Лекция №26 Поточечная сходимость тригонометрического ряда Фурье
- •Лекция №27 Поточечная сходимость тригонометрического ряда Фурье (продолжение)
- •Лекция №28 Собственные интегралы, зависящие от параметра
- •Несобственные интегралы, зависящие от параметра
- •Лекция №29 Несобственные интегралы, зависящие от параметра (продолжение)
- •Лекция №30 Свойства несобственных интегралов, зависящих от параметра
- •Свойства гамма-функции
- •Лекция№31 Преобразование Фурье
- •Разложение в ряд Тейлора-Маклорена некоторых элементарных функций
Лекция №5 Ряды вида
Преобразование Абеля
Пусть дан ряд
![]() (1).
(1).
Введём преобразования Абеля
![]()
Доказательство.
![]()
![]()
Доказано.
С помощью преобразования Абеля доказываются следующие признаки сходимости ряда (1).
Признак Дирихле.
Если
 невозрастающая
и стремится к нулю
невозрастающая
и стремится к нулю
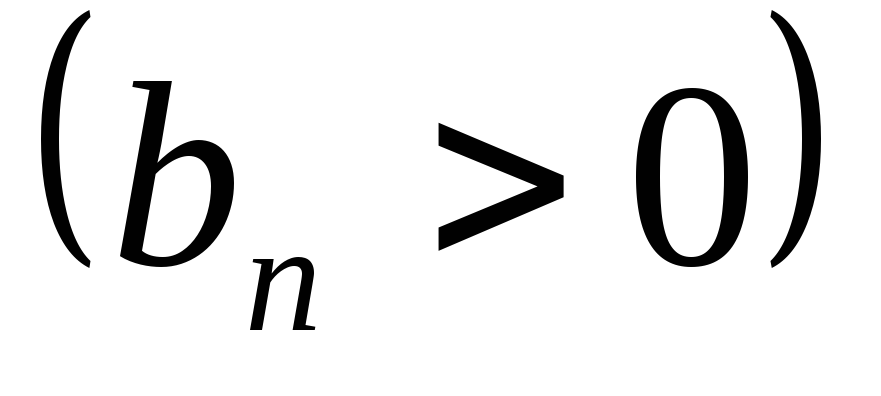 ;
; ограниченная,
ограниченная,
то ряд (1) – сходится.
Доказательство. Воспользуемся критерием Коши и будем оценивать суммы:
![]() (по
преобразованию Абеля)
(по
преобразованию Абеля)
![]()
 и
по критерию Коши ряд (1) сходится.
и
по критерию Коши ряд (1) сходится.
Доказано.
Признак Абеля.
Если
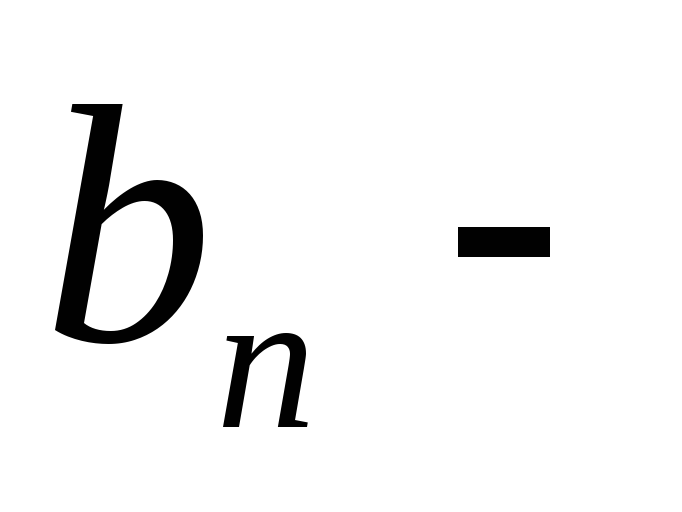 монотонная
и ограниченная;
монотонная
и ограниченная;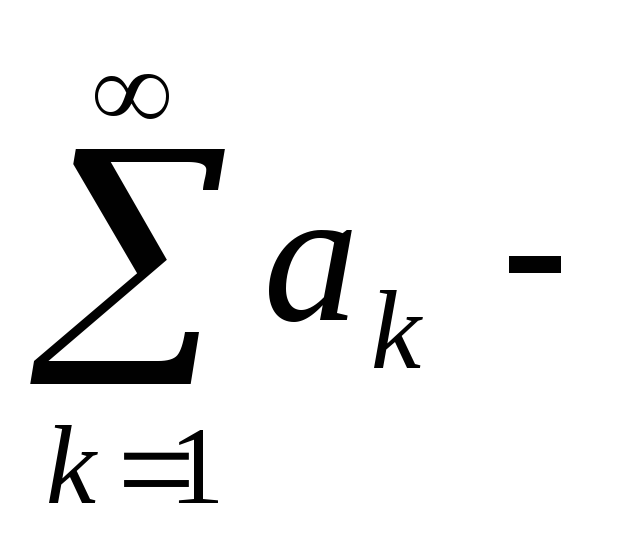 сходится,
сходится,
то ряд (1) – сходится.
Доказательство аналогично доказательству признака Дирихле.
Частным случаем признака Дирихле является признак Абеля.
Если
![]() монотонно
убывает и стремится к нулю, то
монотонно
убывает и стремится к нулю, то![]() сходится
(2).
сходится
(2).
![]() ограниченные,
значит ряд (2) сходится.
ограниченные,
значит ряд (2) сходится.
Рассмотрим ряд
![]()
Оценим суммы
![]()
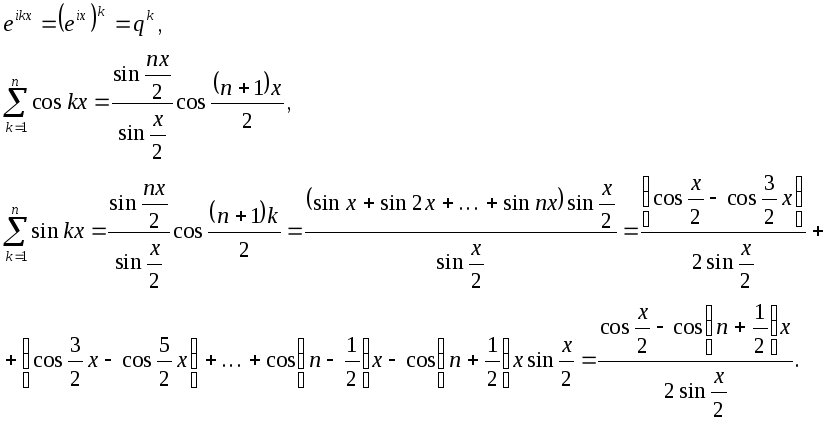
Справедливы оценки

 и
по признаку Дирихле ряд сходится.
и
по признаку Дирихле ряд сходится.
Задача. Исследовать
на сходимость ряд
![]()
Указание.
Рассмотреть
![]()
Лекция №6 Перестановки числовых рядов
Биекция
![]() называетсячисловой
перестановкой N.
называетсячисловой
перестановкой N.
Если
![]() числовой
ряд (1), то ряд вида
числовой
ряд (1), то ряд вида![]() называется
его перестановкой.
называется
его перестановкой.
Пример.
![]() называется егоперестановкой.
называется егоперестановкой.
![]()
Если ряд (1) сходится для любой перестановки и к той же сумме, то он называется безусловно сходящимся.
Теорема Римана.
Если ряд (1)
сходится условно, то
![]() и
существуют перестановки, для которых
представленный ряд расходится.
и
существуют перестановки, для которых
представленный ряд расходится.
Введем некоторые обозначения:
![]()
Доказательство.
Пусть ряд
(1) – сходится условно,
![]()

В итоге построен
ряд
 .
Получили ряд, являющийся перестановкой
исходного ряда.
.
Получили ряд, являющийся перестановкой
исходного ряда.
Нужно показать,
что эта перестановка сходится к числу
S.
Возможны
четыре случая, пусть
![]() тогда
тогда
 ;
;


Оценим разность
![]() в
каждом из четырёх случаев.
в
каждом из четырёх случаев.
Доказано.
Ряд (1) называется
универсальным
относительно
перестановок, если
![]()
Теорема (об универсальных рядах). Ряд (1) – универсальный относительно перестановок
Следствие: условно сходящийся ряд является универсальным относительно перестановок.
Задача. Проверить выполнение условий (1), (2) теоремы об универсальных рядах для условно сходящегося ряда.

противоречие.
Можно определить
и другие понятия универсального числового
ряда, например, универсальный относительно
знака: ряд (1) – универсальный относительно
знака, если
![]()
Задача. Пусть ряд
![]() сходится.
Что можно сказать о сходимости рядов
сходится.
Что можно сказать о сходимости рядов![]()
Ряд ![]() не
обязан сходиться, например
не
обязан сходиться, например
![]()
Ряд ![]() также
не обязан сходиться.
также
не обязан сходиться.
Теорема (о безусловной сходимости). Ряд (1) – сходится безусловно тогда и только тогда, когда ряд (1) сходится абсолютно.
Доказательство. Необходимость.
(1) – сходится безусловно (от противного) (1) – сходится условно (по теореме Римана) (1) – не сходится безусловно – противоречие (1) – сходится абсолютно.
Достаточность.
![]() перестановка
перестановка
![]()
 Доказано.
Доказано.
Замечание. Для абсолютно сходящегося ряда модуль суммы будет:
![]() т.к.
т.к.
![]() при
при![]()
Лекция №6 Перестановки числовых рядов (продолжение)
Группировка числового ряда
Для числового ряда
(1)
![]() группировка
ряда – это ряд вида
группировка
ряда – это ряд вида![]()
Теорема. Любая группировка сходящегося ряда – сходится.
Доказательство. Последовательность частичных сумм группировки является подпоследовательностью частичных сумм исходного ряда и для сходящегося ряда имеет конечный предел. Любая группировка сходящегося ряда сходится к сумме ряда. Обратное утверждение не верно.
Доказано.
Пример. Ряд
![]() расходящийся, но
расходящийся, но![]() сходится.
Или
сходится.
Или![]() сходится.
сходится.
Умножение рядов
Пусть даны два
ряда
![]() (1),
(1),![]() (2).
(2).
Образуем бесконечную
таблицу

Элементы этой таблицы можно вытянуть в линию (занумеровать) бесконечно многими способами. Все они будут по отношению друг к другу перестановками. Этой бесконечной таблице соответствует бесконечно много переставленных числовых рядов. Если некоторые (-ая) перестановка (-и) сходится абсолютно, то все перестановки будут также сходится абсолютно к одной и той же сумме. В этом случае любую перестановку естественно назвать произведением рядов (1) и (2),а её сумму – суммой произведения исходных рядов.
Теорема. Если ряд (1) сходится абсолютно к А, а ряд (2) сходится абсолютно к В, то определено произведение рядов (1) и (2), равное АВ.
Доказательство.
Пусть сумма
(3)
![]() некоторая
перестановка бесконечной таблицы, где
и
- перестановки
N
– множества натуральных чисел.
некоторая
перестановка бесконечной таблицы, где
и
- перестановки
N
– множества натуральных чисел.
Покажем, что (3)
сходится абсолютно:
![]() Можно оценить сверху следующим образом:
Можно оценить сверху следующим образом:![]()
![]() сходится.
сходится.
Остаётся выяснить,
чему равна сумма произведений. Для этого
достаточно взять произвольную перестановку
и в этой перестановке – любую
подпоследовательность частичных сумм.
Возьмём следующую:
![]()
Доказано.

Формальным
произведением,
или произведение
Коши рядов
(1) и (2) называется сумма ряда (3)
![]() Отметим,
что формальное произведение является
группировкой некоторой перестановки
бесконечной таблицы. Поэтому из предыдущей
теоремы и теоремы о группировке
сходящегося ряда вытекают следующие
утверждения:
Отметим,
что формальное произведение является
группировкой некоторой перестановки
бесконечной таблицы. Поэтому из предыдущей
теоремы и теоремы о группировке
сходящегося ряда вытекают следующие
утверждения:
теорема Коши: если ряд (1) сходится абсолютно к А и ряд (2) сходится абсолютно к В, то ряд (3) сходится к
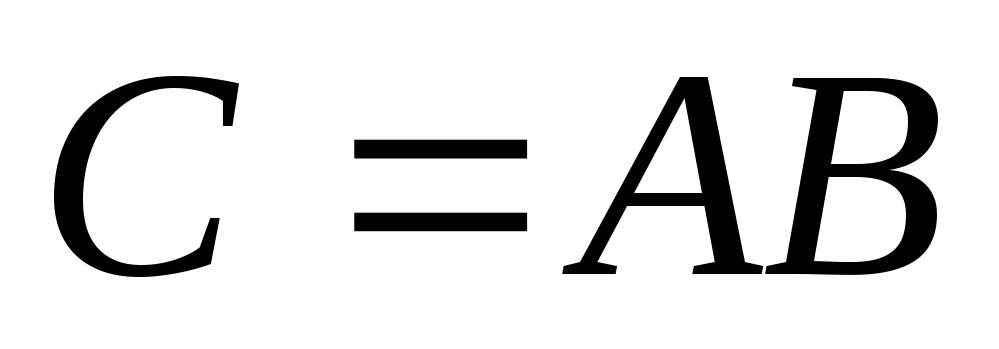 ;
;теорема Мертенса: если ряд (1) сходится абсолютно к А и ряд (2) сходится к В, то ряд (3) сходится к
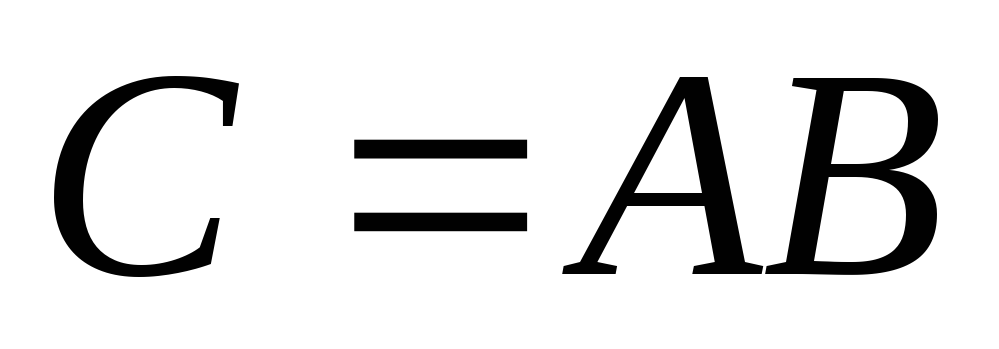 ;
;теорема Абеля: если ряд (1) сходится к А и ряд (2) сходится к В, то ряд (3) сходится к
 .
.
