Лекция №3 Сходимость положительных рядов (продолжение)

1. Признак Даламбера с использованием нижнего и верхнего предела

1. Если 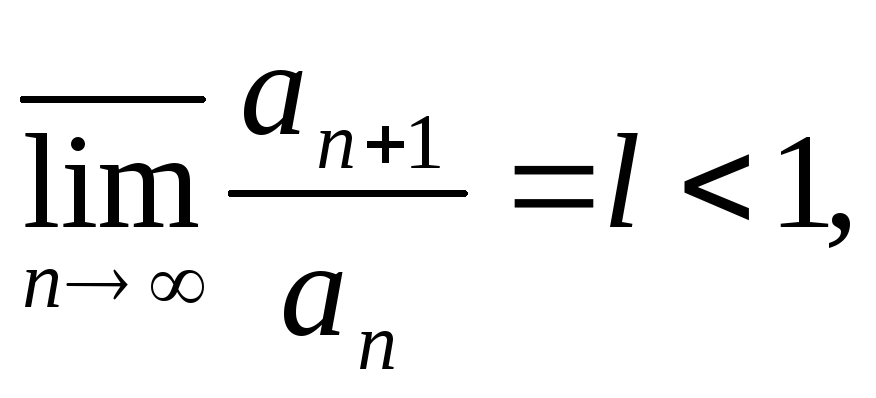то ряд сходится.

2. Если то ряд расходится и

В признаке Даламбера исследуются отношения и в случае нужно уточнение этого представления. Предположим, что имеет место уточнение Если , то ряд сходится, а принельзя сделать определённого вывода; нужно некоторое уточнение. Указанный признак сходимости называетсяпризнаком Раабе.

Объединённый признак Раабе и Даламбера называют признаком Гаусса:

1. ряд расходится;

2. ряд сходится;

3. ряд сходится;

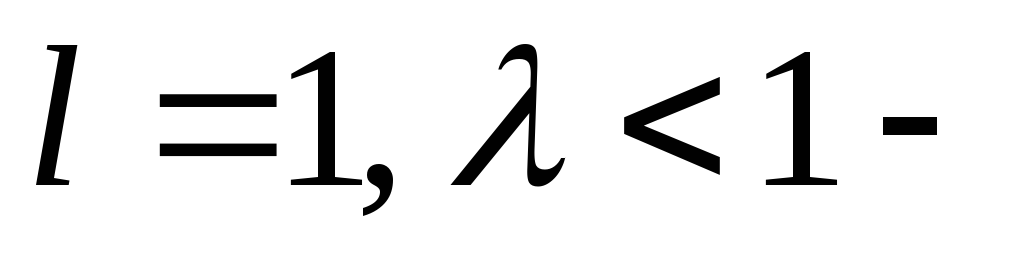4. ряд расходится.

Доказательство (признак Раабе). Доказательство основано на применении обобщённого признака сравнения при сравнении с обобщённым гармоническим рядом .

Пусть сходится. Имеем:

Доказано.

Пример. Исследовать сходимость ряда в зависимости от параметра р .

если ряд сходится;

ряд расходится;

при нужны дополнительные исследования.

Применим формулу Стирлинга

ряд расходится;

ряд сходится.

2. Радикальный признак Коши

Пусть тогда:

1) ряд сходится;

2) ряд расходится

Доказательство. Верхний предел последовательности – это наибольший частичный предел, или

1)

2)

Если и для

и по признаку сравнения со сходящейся геометрической прогрессией данный ряд сходится.

Пусть идля

Доказано.

Радикальный признак Коши «сильнее», чем признак Даламбера, т.е. любой ряд, который можно исследовать при помощи признака Даламбера, можно и исследовать при помощи признака Коши. Но есть такие ряда, которые нельзя исследовать при помощи признака Даламбера, но можно исследовать при помощи признака Коши.

Пример.

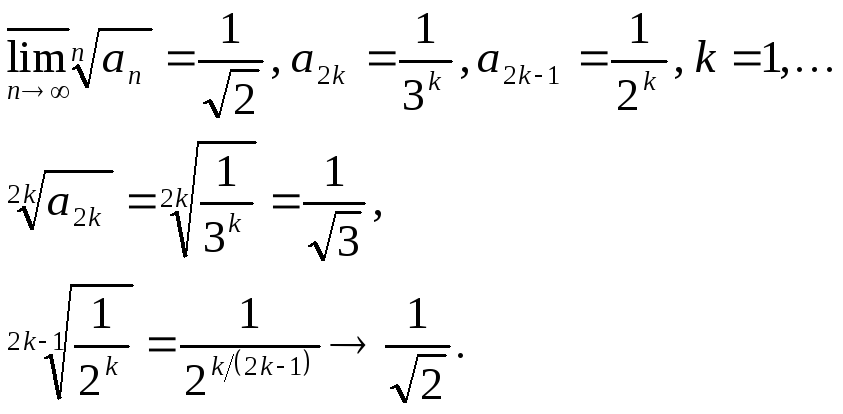
По радикальному признаку Коши ряд сходится.

Используем признак Даламбера.

Получаем неясность.

3. Признак Коши для рядов с монотонными членами

Пусть невозрастающая

Тогда -сходится сходится.

Доказательство. Необходимость.

Пусть ряд – сходится  ограниченная

ограниченная  ряд – сходится.

Достаточность.

Пусть ряд – сходится  ограниченная

ограниченная  ряд -сходится.

Пример 1. убывающая.

сходится

Пример 2. сходитсясходится при

Лекция №4 Сходимость положительных рядов (продолжение)

1. Интегральный признак Коши

Пусть невозрастающая. Тогда ряд сходится

сходится и для остатка

Пример. сходится.

сходится.

Доказательство. Будем использовать геометрическую интерпретацию.

или

Так как сходимость ряда эквивалентны ограниченности и, то утверждение признака вытекает из этих неравенств.

Оценим остаток.

Доказано.

Пример. Исследовать сходимость .

при расходится. Значит, исходный ряд расходится.

Ряды с членами произвольного знака

ряд с положительными членами (2)

Ряд (1) называется абсолютно сходящимся, если сходится ряд (2).

1. Признак абсолютной сходимости

Абсолютно сходящийся ряд является сходящимся.

Доказательство. Основано на применении критерия Коши.

Ряд (2) – сходится  (по критерию Коши) 

 (по критерию Коши)  ряд (1) – сходится. Доказано.

Сходящийся ряд (1) называют условно сходящимся, если он абсолютно расходится.

Существуют условно сходящиеся ряды.

Рассмотрим класс знакочередующихся рядов: (3).

Признак Лейбница.

Если для ряда (3) выполнены условия:

1. невозрастающая;

2. 

то ряд (3) сходится и справедлива оценка остатка

Доказательство. Рассмотрим

т.е. неубывающая. С другой стороны

Итак, последовательность неубывающая и ограниченная сверху и. Для последовательности частичных сумм с нечётными номерамиЗначит,

Остаётся оценить остаток:

Доказано.

Пример.

расходится

Исходный ряд сходится условно.