
Дискретная математика
.pdf
vk.com/club152685050 | vk.com/id446425943
Пример.
x
Граф- планарный, т.к. его можно изобразить без видимых пересечений ребер:
x
S=4, W= 5 – 7 + 4 = 2.
Теорема (об эйлеровой характеристике планарного графа)
Эйлерова характеристика любого планарного связного графа равно двум,
т.е.
|M|-|Г|+ S = 2.
б/д
Теорема (необходимый признак планарности графа).
Для всякого связного планарного графа без петель и кратных ребер справедливо неравенство.
|Г| 3|M| - 6
Доказательство.
Каждая грань графа G ограничена, как минимум, тремя ребрами, а каждое ребро является границей не более двух граней,
Из Теоремы. об эйлеровой характеристике имеем:
|M| - |Г| + S = 2 3|M| - 3|Г| + 3S = 6 |
|
3S= 3|Г| - 3|M| + 6 2 |Г| |
|
|Г| 3|M| - 6 |
|
|
|
|
|
|
ч.т.д. |
Следствие: Если для графа G=<М,Г> выполняется |Г|>3|M| - 6, то граф не является планарным.
Теорема Куратовского
Граф является планарным тогда и только тогда, когда он не содержит подграфов, стягиваемых к графам.
91

vk.com/club152685050 | vk.com/id446425943
Стягивание ребра – операция, которая удаляет ребро из графа а инцидентные этом ребру вершины сливаются в одну.
Утверждение.
Любой граф, содержащий конечное или счетное число ребер может быть изображен без пересечений в трехмерном пространстве.
Пример.
Проверить необходимое условие планарности для графов из теоремы Куратовского.
1)|M|=6; |Г|=9; 9 12 – выполняется (но это не достаточное условие)
2)|M|=54; |Г|=10; 10>3*5-6 – т.е не выполняется
§ 8.Задача о раскраске графа
В 1878 на заседание английского Королевского общества математик Артур Кэли сформулировал задачу: Можно ли на политико-административной карте раскрасить страны так, чтобы никакие две страны, имеющие общую границу, не были раскрашены одно краской, и при этом было бы использовано не более 4-х цветов.
Опр. Раскраской графа без петель и кратных ребер называется сопоставление красок вершинам графа.
Раскраска называется правильной, если любые две смежные вершины
графа окрашены в разные цвета. |
|
|
Наименьшее число цветов, для |
которого |
существует правильная |
раскраска вершин графа G называется |
хроматическим числом графа G: χ(G) |
|
В настоящее время задача, поставленная Кэли решена т.е. доказано, что хроматическое число любого планарного графа не превышает четырех.
Утверждение.
Хроматическое число планарного графа χ (G)=2 т. и т.т., когда граф не содержит циклов нечетной длины.
92
vk.com/club152685050 | vk.com/id446425943
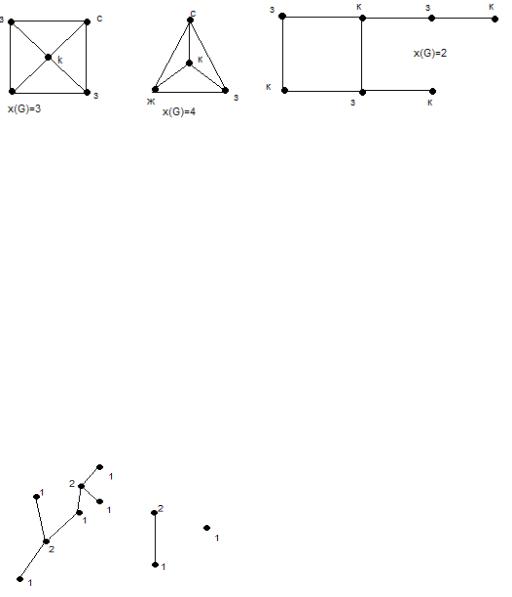
Пример.
Найти χ (G) графов:
Алгоритм последовательной раскраски:
1.Произвольная вершина ai графа G принимает цвет №1.
2.Если все вершины графа раскрашены то задача выполнена, если нет, то перейти к п.3.
3.Если не раскрашенная вершина ai , смежна с одной из уже
раскрашенных, то ей присваивают минимальный номер цвета, не совпадающего с номером цвета смежных с ней вершин, перейти к п.2.
Этот алгоритм не всегда приводит к минимальной (в смысле количество цветов) раскраске.
Утверждение. Если G – лес, то χ(G) 2.
Любая не раскрашенная вершина графа G не может быть смежна двум раскрашенным, т.к. это означало бы существование цикла в G.
§9. Эйлеров цикл. Гамильтонов цикл
Опр. Цикл в графе G называют эйлеровым, если он проходит по одному разу через каждое ребро графа. Граф, содержащий эйлеров цикл, называется
эйлеровым графом.
Теорема (об эйлеровых циклах).
Для того, чтобы в связном графе без петель существовал эйлеров цикл, необходимо и достаточно, чтобы степени всех его вершин были четными.
93
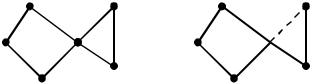
vk.com/club152685050 | vk.com/id446425943
Доказательство.
Основано на том, что вход в любую вершину и выход из нее осуществляется по разным ребрам deg xi 2k четна
Замечание. Задача о Кёнигсбергских мостах не имеет решения (не существует Эйлеров цикл)
Опр. Цикл в графе называется гамильтоновым, если он проходит все вершины графа по одному разу.
Опр. Граф G называют полным, если все его вершины смежные.
Замечание: В полном графе |Г|= |
| M | (| M | 1) |
|
2 |
||
|
Теорема (достаточное условие существования гамильтонова цикла).
Если граф G полный, то в нем существует гамильтонов цикл.
Доказательство. Пусть дан G=<М,Г>; M {x1 , x2 ,....xn } т.к. все вершины смежные, то можно построить цикл x1 x2 ,x3 ... xn x1
Так как нет повторяющихся ребер и вершин (кроме первой и последней), то построенный цикл – гамильтонов.
Опр. Точкой сочленения графа G называется такая вершина, удаление которой вместе с инцидентными ей ребрами увеличивает число компонент связности.
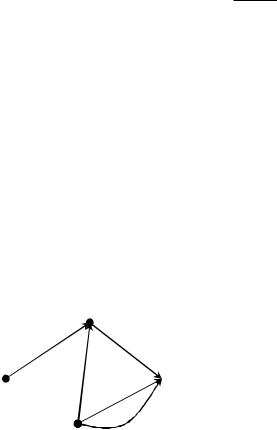
Пример.
x
x-( ) сочленения
Теорема (Необходимое условие существования гамильтонова цикла).
Если в графе G существует гамильтонов цикл, то это связный граф без точек сочленения.
Доказательство:
1) Связность: т.к. в существует гамильтонов цикл, то все вершины графа являются соединенными граф связный.
94
vk.com/club152685050 | vk.com/id446425943
2) В графе G нет точек сочленения: Проведем доказательство от противного: Пусть в связном графе, содержащем гамильтонов цикл, существует точка сочленения xi .
Удалим из графа G вершину xi вместе с инцидентными ей ребрами, тогда цикл превратиться в цепь, содержащую все вершины кроме xi , т.е. граф останется связным, что противоречит тому, что xi является точкой сочленения.
ч.т.д.
Замечание.
Задача нахождения гамильтонова цикла математически неразрешима.
Задача о коммивояжере
Коммивояжеру необходимо посетить несколько населенных пунктов, расстояние между которыми известно. Требуется найти кратчайший маршрут, проходящий по всем населенным пунктам по одному разу, и вернуться в исходный пункт.
Задача решается нахождением всех гамильтоновых циклов и выбором из них наименьшего.
Пусть G=<М,Г> - полный, тогда в нем существует (n 1)! гамильтоновых
2
циклов (Выберем одну вершину графа, остальные n-1 вершин можно произвольным образом расставить (n-1)! способами; делим на 2 т.к. направление не учитывается).
§10. Ориентированный граф (орграф)
|
|
|
|
Опр. Ориентированным графом называют совокупность |
G M , Г |
где |
|
М- непустое конечное множество элементов, называемых вершинами орграфа;
|
|
|
|
|
|
|
Г |
- множество упорядоченных |
пар |
вершин |
(x,y)= , |
называемых дугами |
|
|
орграфа. |
|
|
|
|
|
|
Рассмотрим на примере способы задания орграфа |
|
||||
|
|
|
X2 |
|
|
|
|
γ1 |
|
γ2 |
|
|
|
|
X1 |
γ5 |
γ4 |
X3 |
|
|
|
|
|
|
|
|
|
|
|
X4 |
γ3 |
|
|
|
|
|
|
G |
M , Г |
||
1. Перечисление элементов множества:
95

vk.com/club152685050 | vk.com/id446425943
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M {x1 , x2 ,.x3 , x4 } , Г |
={ |
1 , |
2 , |
3 , |
4 , 5 }, где 1 |
=( x1, x2 ); |
2 =( x2 ,.x3 ), |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 ( x3 , x4 ), |
4 |
|
( x4 , x3 ), |
5 |
( x4 , x2 ) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k, (x , x |
|
) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
|
|
|
|
2. Матрица смежности S {Sij }, где Sij |
|
|
|
|
|
|
|
|
||||||||||||
кратности k |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, (x , x |
|
Г |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
|
|
|
|
x1 |
x2 |
|
x3 |
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
0 |
1 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S= x2 |
0 |
0 |
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
0 |
0 |
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
0 |
1 |
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
x - начало дуги |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. Матрица инцидентности |
R {rij }, где rij |
|
|
- конец дуги |
|
|
|
|||||||
1, xi |
j |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
не инцидентна |
|
вершине xi |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
x1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
R= |
x2 |
1 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x3 |
1 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
x4 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства матриц смежности и инцидентности орграфа
Опр. Полустепенью исхода вершины x называют число выходящих из вершины х дуг: deg_x; полустепенью захода называют число заходящих в х дуг: deg+x
Сумма по столбцам матрицы инцидентности орграфа без петель равна 0.
Для орграфа без петель сумма по столбцам матрицы смежности равна числу заходящих в соответствующие вершины дуг
k
Sij deg x j j 1
k
Сумма по строкам: Sij deg x j -число выходящих из вершины дуг
j 1
96

vk.com/club152685050 | vk.com/id446425943
|
|
|
х1 |
х2 |
х3 |
х4 |
|
deg xi |
|
|
|
х1 |
0 |
1 |
0 |
0 |
1 |
||
|
|
х2 |
0 |
0 |
1 |
0 |
1 |
||
S |
= |
х3 |
0 |
0 |
0 |
1 |
1 |
||
х4 |
0 |
1 |
1 |
0 |
2 |
||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
deg xi |
0 |
2 |
2 |
1 |
|
5 | Г | |
|
Теорема Эйлера (для орграфа). |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
число дуг графа, тогда сумма |
|
Пусть |
G M , Г - орграф без петель, |
Г |
|||||||
полустепеней исхода всех вершин графа равна сумме полустепеней захода и равна количеству дуг:
n |
n |
|
deg xi |
deg xi |
| Г | |
i 1 |
i 1 |
|
Замечание. Матрица смежности орграфа не обязательно симметрична.
§ 11. Задача о минимальном пути
|
|
|
G M , Г |
- орграф. |
|
Опр.
|
1) |
Ориентированным |
маршрутом |
в орграфе |
|
|||
|
G |
|||||||
последовательность |
вершин |
и |
связывающих |
|
||||
xi |
, (xi xi2 ), xi |
(xi |
2 |
, xi ),...(xi |
, xin ), xin |
|
|
|
1 |
1 |
2 |
3 |
n 1 |
|
|
|
|
называют их дуг:
2)Незамкнутый ориентированный маршрут в котором все дуги различны называются путем, замкнутый – контуром.
3)Путь или контур называются простыми, если в них все вершины
различны.
Замечание. Если граф G не имеет петель и кратных дуг, то любой путь в нем однозначно задается последовательностью вершин (дуги можно не указывать)
Опр. Вершина x j называется достижимой из вершины x j , если существует путь xi ,...x j (Аналог “соединенности вершин” в неорграфе)
Для орентированных графов справедлива
97
vk.com/club152685050 | vk.com/id446425943
Теорема (о свойствах матрицы смежности орграфа)
Пусть S-матрица смежности орграфа , S n s(n) , тогда элемент s( n)
G ji ji
матрицы S n равен количеству путей из вершин xi в вершину x j .
Доказательство аналогично доказательству соответствующей теоремы для неориентированного графа.
Пример: Определит количество путей длины 2 и длины 3 из x1 в x3 .
x2
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 1 |
1 |
1 1 |
|
1 |
|
2 2 |
|||
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
S |
|
0 |
1 1 ; S 2 |
|
1 |
1 1 |
; S 3 |
1 |
|
2 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 0 |
|
0 |
1 1 |
|
1 |
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S (2) |
1 П x x |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
13 |
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
S (3) |
2 П x |
x |
2 |
x |
2 |
x |
|
|
|
|
|
|
|
|
|||||||||
|
13 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||
|
|
|
П2 x1 x3 x1 x3 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Опр. |
Орграф |
|
G =<М, |
Г |
> называется нагруженным (взвешенным), если |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на множестве его дуг задана неотрицательная функция |
( ) |
; |
при этом число |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называется число ( )= |
||||
( i ) |
называется длиной дуги |
i |
. Длинной пути П. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( i ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Опр. |
Путь в нагруженном орграфе G |
из вершины х вершин у называется |
|||||||||||||||||||||
минимальным, если он имеет наименьшую длину из всех существующих путей из х в у
Свойства минимальных путей
1.Если путь { xi11, xi 2,....xin } из xi1 в xin } является минимальным, то любой
участок этого пути { xik ,...xi ( k m) } где |
1 k k m n, будет минимальным |
путем |
||
из xik в xi ( k m ) |
|
|
|
|
2. |
Если путь { xi1 xi 2 … xin , xin 1 } - минимальный путь из |
xi1 в xin 1 |
среди |
|
всех путей, содержащих не более n дуг, то путь {xi1 ,...xin } является минимальным среди всех путей из xi1 в xin , содержащих не более (n-1) дуги.
98

vk.com/club152685050 | vk.com/id446425943
§ 12. Алгоритм Форда-Белмана (построение минимального пути).
|
|
|
|
|
|
|
|
|
|
|
Пусть нагруженный орграф G =<М, Г |
> не содержит петель и кратных |
|||||||||
дуг; M {x1 ,...xn } Будем считать что: |
|
|
|
|
|
|
|
|
|
|
1) |
Длина минимального пути из x1 |
в x1 |
за число шагов равна 0. |
|
|
|
||||
2) |
Если не существует пути x1 в xi , то длина минимального пути |
из x1 в |
||||||||
|
xi равна . |
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 |
|
|
|
|
||
|
|
|
s |
|
|
|
|
|
|
|
3) |
В качестве нормы n-мерного вектора S |
|
возьмем ||S||= min s |
|
. |
|||||
|
|
|
|
|
2 |
|
|
1 i n |
i |
|
|
|
|
|
s |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
Введем вспомогательную |
матрицу |
С( G ) |
длин дуг: |
С( G )= |
|||||
Cij , i i, n, j 1, n
|
, x j |
),если (xi , x j |
|||
(xi |
|||||
Cij = |
|
|
|
|
|
|
|
|
|
|
|
|
|
, x |
|
) Г |
|
, если (x |
j |
||||
|
|
i |
|
|
|
)Г
5)обозначим С 1 , C 2 ... C n - столбцы матрицы С( G )
Алгоритм построения матрицы минимальных путей { ij }n x
1.В I строке все элементы равны 0: 1 j 0
Все элементы I столбца, кроме элемента 1 j , равны : i1 , i 1
2.Формируем II столбец матрицы : 12 0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
i 2 |
|| 1 |
Ci ||, i |
2, n , |
где 1 - |
I столбец |
матрицы, Ci |
- i-тый |
столбец |
|||||||||
матрицы С. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Для каждого |
элемента |
i 2 запоминаем |
|
номер |
наименьшего |
элемента |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
столбца |
(1 Ci ) : Ni 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
j) Формируем j-тый столбец матрицы |
|
аналогичным образом: |
1 j =0, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|| j 1 |
Ci ||, i 2, n |
|
j 3, n , |
для |
каждого |
элемента |
ij запоминаем |
номер |
|||||||||
наименьшего элемента Nij
Т.о. за n-шагов построим матрицу минимальных путей.
По матрице восстановим минимальный путь из x1 в х2
99
vk.com/club152685050 | vk.com/id446425943
1)Последней вершиной искомого пути является вершина xn
Элемент матрицы nn равен длине минимального пути; по элементу nn восстановим номер N nn n это номер предпоследний вершины минимального пути, т.е. предпоследняя вершина x n
2) Переходим к предпоследнему столбцу матрицы находим в нем элементы nn 1 , восстанавливаем по номеру N n n 1
… x n 1 x n xn
3) Аналогичным образом восстанавливаем путь до тех пор, пока не окажемся в I столбце матрицы , т.е. пока не доберемся до вершины x1
Построенный таким образом путь – минимальный и содержит не более (n-1) дуги.
Замечание.
Если среди элементов последней строки матрицы найдется элементnj nn , то посторенние минимального пути можно начинать с него. В этом
случае искомый путь содержит не более (j-1) дуг.
Пример.
По алгоритму Форда-Беллмана построить минимальный путь из
x1 в x6 для орграфа G :
|
|
|
x2 |
|
2 |
12 |
|
|
|
|
|
x1 |
|
3 |
3 |
|
|
15
x6 |
|
|
|
|
|
|
|
|
|
|
C1 |
C 2 |
C 3 |
C 4 |
C 5 |
C 6 |
|
|
|
|
|
|
|
|
|
x1 |
|
2 |
12 |
|
|
15 |
|
x2 |
|
|
|
5 |
|
|
C= x3 |
3 |
|
|
|
2 |
3 |
|
|
x4 |
|
|
2 |
|
|
|
|
x5 |
|
|
|
|
|
2 |
|
x6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
2 |
5 |
2 |
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x5 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|||
|
|
|
|
|
|
|
|
|
||
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
|
|
21 |
21 |
21 |
21 |
21 |
|||
= |
|
12 |
12 |
94 |
9 |
4 |
9 |
4 |
||
|
|
|
1 |
1 |
|
|
|
|
||
|
|
|
|
143 |
143 |
113 |
113 |
|||
|
|
|
|
143 |
143 |
113 |
113 |
|||
|
|
|
151 |
151,3 |
151,3 |
123 |
123 |
|||
100
