2. Математические модели роста популяции

1. Модель естественного роста ( модель Мальтуса)

Одна из самых простых математических моделей биологических процессов – модель «естественного роста». Модель не учитывает внутривидовой конкуренции между особями и взаимодействия популяции с другими популяциям.

Основная идея этой модели заключается в том, что скорость роста численности популяции , определяемая скоростью размножения R и скоростью гибели S, прямо пропорциональна самой численности популяции х (например, числу клеток, числу микроорганизмов, числу особей).

= R+ S ~ x,

,

поскольку скорость размножения R и скорость гибели S

пропорциональны численности популяции

R= и , где - коэффициент размножения, а - коэффициент гибели, и поэтому

; ,

где = γ - δ - коэффициент роста.

Решение дифференциального уравнения естественного роста дает:

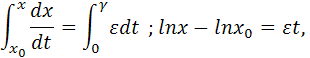
(7.1)

,

где - начальная численность популяции (при t=0).

Таким образом, численность популяции x возрастает экспоненциально со временем (если и ), убывает ( если и ) и сохраяется (если и ), как это показано на рисунке 7.1.

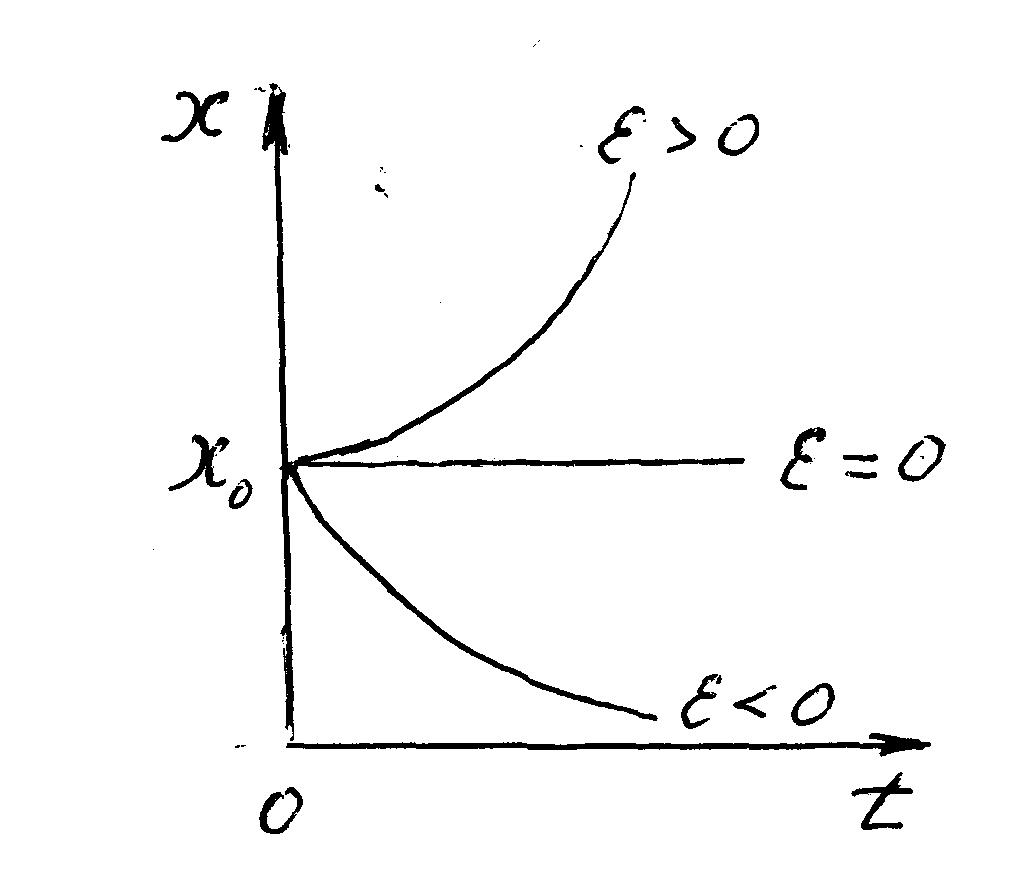
Рис. 7.1. Иэменение численности попуяции во времени согласно модели Мальтуса.

2. Модель Ферхюльста

Согласно модели естественного роста, если скорость рождений хотя бы немного больше скорости роста численности популяции с течением времени скорость роста численности популяции растёт и наконец катастрофически нарастает. Однако как всякая модель, модель естественного роста имеет границы применения. При чрезмерном увеличении численности популяции начинают действовать новые факторы, которые надо учитывать введением в дифференциальное уравнение роста новых членов: теснота, недостаток питания, изменение

вследствие перенаселенности физико-химических параметров среды (температуры, pH, концентрации кислорода, углекислого газа и т.д.), а также в некоторых случаях численность популяции ограничивает наличие хищников.

Внутривидовая конкуренция в популяции учитывается в модели Ферхюльста введением в математическую модель члена , отражающего уменьшение скорости роста численности популяции из-за внутривидовой конкуренции:

(7.2)

При небольших численностях популяции х влияние этого члена незначительно, оно становится заметным при больших х, что приводит к замедлению роста х, и тогда, когда εх = и , устанавливается стационарная численность популяции

( рис. 7.2).

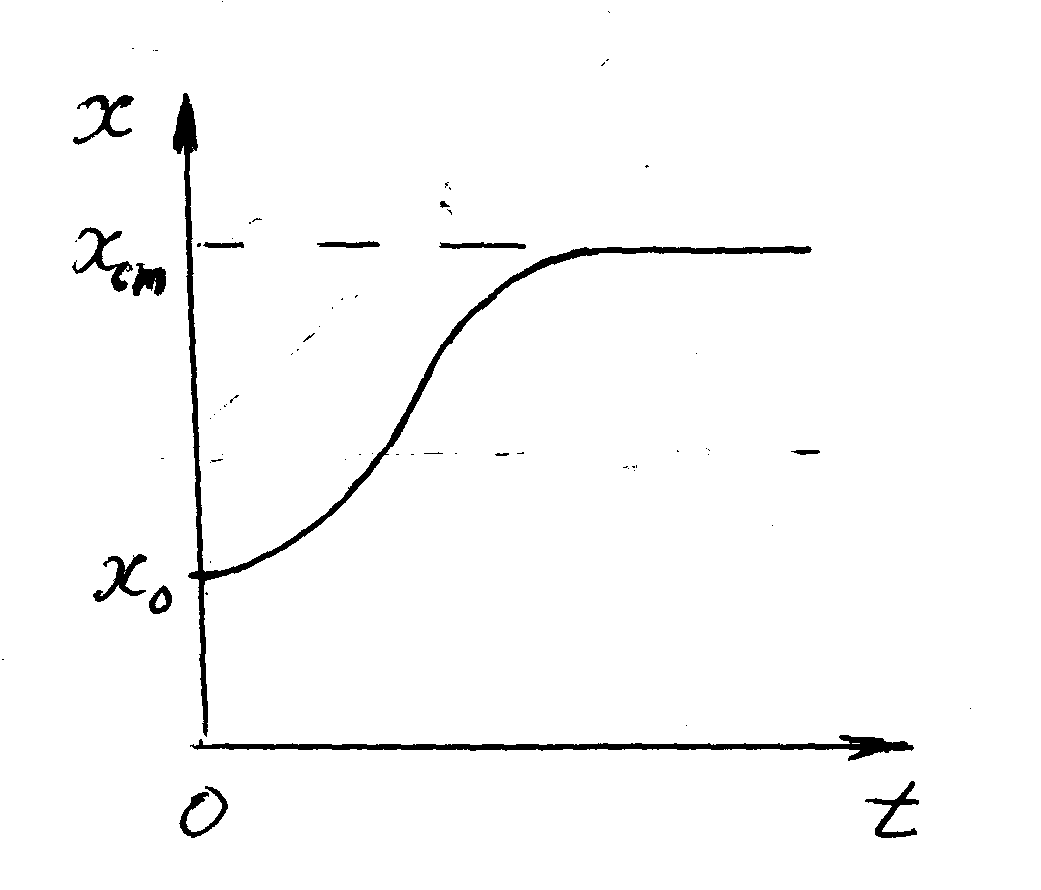
Рис. 7.2. Временная зависимость численности популяции по модели Ферхюльста

3. Модель «жертва – хищник» Вольтерра

Модель изменения численности живых организмов с учетом взаимоотношений жертв и хищников, так называемую модель «жертва – хищник», создал Вольтера, опубликовавший в 1930 году свою известную работу «Математическая теория борьбы за жизнь».

Согласно этой модели скорость изменения численности жертв

(7.3),

а хищников

(7.4) ,

где у – число хищников, х - жертв.

В этих уравнениях кроме скорости естественного роста ( ) учтено уменьшение числа жертв, обусловленное их встречами с хищниками, введением члена ( ), число встреч жертв и хищников тем больше (в первом приближении прямо пропорционально), чем больше число жертв и хищников .

Член ( ) моделирует скорость размножения хищников, которая тем больше (в первом приближении прямо пропорциональна), чем больше число жертв (пищи) и хищников (родителей). Член ( ) – скорость естественной гибели хищников. Количество корма для жертв считается неограниченным. Система жертва-хищник может быть при некоторых условиях саморегулирущейся системой.

В стационарном случае, когда число хищников и жертв не меняется во времени , ,

то есть равны нулю скорости их изменения:

,

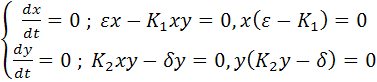У этой системы уравнений есть два решения. Либо х=0 и y=0 – это соответствует равновесному случаю, а равновесие, как известно, смерть живого: нет ни хищников, ни жертв. Либо

и

.

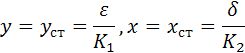
Согласно этой (явно идеализированной модели), если в начальный момент времени число жертв и хищников соответствует стационарным значениям

то система останется в стационарном состоянии, с течением времени x и y не будут меняться.

Если же это условие не соблюдено, система не будет стационарной, число жертв x и хищников y будет меняться. Однако, как выяснилось при анализе математической модели «жертва-хищник», в этом случае система также может остаться саморегулирующейся: и число жертв, и число хищников колеблется около стационарных значений и (рис. 7.3)

Рис. 7.3 Циркуляция состояния системы «хищники-жертвы» около стационарного состояния (а) и колебания числа хищников и жертв около стационарных значений (б) согласно модели «хищник-жертва» Вольтера.

При этом состояние экологической системы, описываемое параметрами x и y, совершает циркуляцию около стационарного состояния ( ) и ( ) (рис. 7.3 а).

Не приводя математические выкладки, качественно процесс саморегуляции системы жертва-хищник можно объяснить так. Если число хищников (например, волков) меньше стационарного (точка 1 на рис. 7.3 а), то скорость естественного роста жертв (например, зайцев) по абсолютной величине превышает скорость их поедания хищниками. Число зайцев будет расти, но одновременно будет расти и число волков из-за переизбытка пищи.

Численность зайцев растет до того момента, пока численность волков не станет столь велика, что это станет уже ограничивать число зайцев (точка 2 на рис. 7.3 а). Затем некоторое время численность волков будет продолжать расти, так как сохраняется избыток их пищи, а численность зайцев будет уменьшаться, пока это в конце концов не приведёт и к сокращению численности волков из-за недостатка пищи (точка 3 на рис. 7.3 а). Когда волков станет достаточно мало, зайцы опять начнут увеличиваться в своей численности (точка 4 на рис.7.3 а) и так далее.

Приблизительно зависимость от времени численности жертв x (t) и хищников y (t) можно представить:

( рис. 7.3 б)

Как показывает математический расчет, частота циркуляций состояния системы вокруг стационарного состояния (рис. 7.3а):

А соотношение амплитуд колебаний численности хищников А_у и А_х:

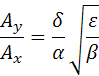
Численности хищников и жертв испытывают периодические колебания с одинаковой частотой. Колебания y отстают по фазе от колебаний x.

На рис. 7.4 приведены данные об изменении численности зайцев и рысей в Канаде за 1845-1935 гг., полученные на основе количеств заячьих и рысьих шкур, поступивших в канадские фактории. (Рыси в Канаде, повидимому, питались в основном зайцами, а шкуры других любителей зайчатины волков в факториях не ценились).

Рис. 7.4. Динамика популяций зайцев и рысей в Канаде.

Как видим, в реальном случае временные зависимости численности зайцев (жертв) и рысей (хищников) более сложные, чем это следует из абстрактной модели, тем более поразительно, что основные качественные выводы из этой сравнительно простой модели подтверждаются: происходят с одинаковой частотой колебания численностей хищников и жертв, и эти колебания смещены по фазе относительно друг друга.

Сам Вольтерра пришёл к основным идеям своей теории, анализируя динамику появления рыб различных пород на средиземно-морских рынках (это он делал по просьбе своего брата – рыботорговца). В этом случае тоже наблюдаются характерные взаимосвязанные колебания численности жертв и хищников.

Таким образом, экологические системы способны к саморегуляции (правда, при не очень большом удалении от стационарного состояния). При сильных отклонениях от стационарного состояния (в результате каких-либо природных катастроф: например, резкого изменения климата, но чаще в результате грубого и неумелого вмешательства человека) система теряет способность к саморегулированию. Например, при полном уничтожении хищников, ограничивающих численность некоторых видов, численность этих популяций катастрофически возрастает. ( Так, например случилось в средневековой Европе, когда во время «ведьминских» процессов стали уничтожать «слуг дьявола» - кошек. За это люди были наказаны эпидемией чумы, потому что резко возросло поголовье крыс – разносчиков чумы. В прошлом веке в Китае, когда началось гонение на воробьёв, размножились вредные гусеницы).

Модель Вольтера применялась к бактериям и бактериофагам. Во всех нас есть возбудители болезней, но в здоровом организме эти «жертвы» находятся под контролем «хищников» - нашей иммунной системы. Количества этих «жертв» и «хищников» колеблются около стационарных значений с небольшими амплитудами. При больших отклонениях от стационарного состояния, происходят заболевания.