
тест дискретка 3
.pdf
vk.com/club152685050 | vk.com/id446425943
Вариант 3
№ |
|
|
Вопросы |
Варианты ответов |
||||||
п.п. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
Булева функция «Логическое умножение» |
1. |
Дизъюнкцией; |
|||||||
|
иначе называется … |
2. |
Эквивалентностью; |
|||||||
|
|
|
|
|
3. |
Конъюнкцией; |
|
|
|
|
|
|
|
|
|
4. |
Импликацией; |
|
|
|
|
|
|
|
|
|
5. |
Штрих Шеффера. |
||||
2 |
Сколько существует булевых функций от |
1. |
Четыре; |
|||||||
|
двух переменных? |
2. |
Восемь; |
|||||||
|
|
|
|
|
3. |
Шестнадцать; |
|
|
|
|
|
|
|
|
|
4. |
Тридцать две; |
|
|
|
|
|
|
|
|
|
5. |
Шестьдесят четыре. |
||||
3 |
Сколько существует булевых функций от |
1. |
Шестнадцать; |
|||||||
|
трёх переменных? |
2. |
Тысяча двадцать четыре; |
|||||||
|
|
|
|
|
3. |
Тридцать две; |
||||
|
|
|
|
|
4. |
Пятьсот двенадцать; |
||||
|
|
|
|
|
5. |
Двести пятьдесят шесть. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
4 |
Булева функция задана таблицей истинности |
1. |
Эквивалентностью; |
|
||||||
|
x |
y |
f |
|
2. |
Стрелкой Пирса; |
|
|||
|
0 |
0 |
1 |
|
3. |
Импликацией; |
||||
|
0 |
1 |
0 |
|
4. |
Сложением по модулю два; |
||||
|
1 |
0 |
0 |
|
5. |
Дизъюнкцией. |
||||
|
1 |
1 |
1 |
… |
|
|
|
|
|
|
|
Функция называется |
|
|
|
|
|
|
|||
5Булева функция задана таблицей истинности
x |
y |
f |
|
|
|
|
|
1. |
Конъюнкцией; |
||||
0 |
0 |
0 |
|
2. |
Стрелкой Пирса; |
|
0 |
1 |
0 |
|
3. |
Импликацией; |
|
1 |
0 |
0 |
|
4. |
Сложением по модулю два; |
|
1 |
1 |
1 |
… |
5. |
Дизъюнкцией. |
|
Функция называется |
|
|
|
|||
6Булева функция задана таблицей истинности
|
x |
y |
f |
|
1. |
Конъюнкцией; |
||
|
0 |
0 |
1 |
|
2. |
Дизъюнкцией; |
||
|
0 |
1 |
1 |
|
3. |
Импликацией; |
модулю два; |
|
|
1 |
0 |
0 |
|
4. |
Сложением по |
||
|
1 |
1 |
1 |
… |
5. |
Штрих Шеффера. |
||
|
Функция называется |
|
|
|
|
|||
7 |
Булева функция задана таблицей истинности |
1. |
Конъюнкцией; |
|||||
|
x |
y |
f |
|
2. |
Дизъюнкцией; |
||
|
0 |
0 |
1 |
|
3. |
Импликацией; |
||
|
0 |
1 |
1 |
|
4. |
Эквивалентностью. |
||
|
|
|
|
|
5. |
Тождественной единицей. |
|
|
|
1 |
0 |
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|

vk.com/club152685050 | vk.com/id446425943
Функция называется …
8 |
Из колоды карт в 36 штук вытаскивают 2. |
1. 72; |
|
|
|
|
|
|
|
||||||
|
Сколько исходов можно наблюдать? |
2. 216; |
|
|
|
|
|
||||||||
|
|
|
|
|
|
3. |
1024; |
|
|
|
|
||||
|
|
|
|
|
|
4. |
64; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
630. |
|
|
|
|
|
|
|
9 |
Имеются две прямые. На первой прямой |
1. |
75; |
|
|
|
|
|
|
||||||
|
выбраны 7 точек, на второй - 5. Сколько |
2. |
35; |
|
|
|
|
|
|
||||||
|
треугольников можно построить с |
3. |
70; |
|
|
|
|
|
|
||||||
|
вершинами в указанных точках? |
|
4. 175; |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
5. |
2070. |
|
|
|
|
|
|
|
10 |
Вычислить |
. |
|
|
1. |
80; |
|
|
|
|
|
|
|||
|
|
|
2. |
6; |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
3. |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
20; |
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
100. |
|
|
|
|
|
|
||
11 |
Аббревиатура СДНФ расшифровывается |
|
1.Современная |
||||||||||||
|
как … |
|
|
|
|
дифференциальная нормальная |
|||||||||
|
|
|
|
|
|
|
форма; |
||||||||
|
|
|
|
|
|
2. |
Совершенная |
||||||||
|
|
|
|
|
|
|
дифференциальная нормальная |
||||||||
|
|
|
|
|
|
|
функция; |
||||||||
|
|
|
|
|
|
|
3. |
Совершенная дизъюнктивная |
|
|
|||||
|
|
|
|
|
|
|
нормальная форма; |
диффузионная |
|||||||
|
|
|
|
|
|
|
4.Совершенная |
||||||||
|
|
|
|
|
|
|
нормальная форма; |
||||||||
|
|
|
|
|
|
5. |
Своевременная |
||||||||
|
|
|
|
|
|
|
дизъюнктивная нормальная |
||||||||
|
|
|
|
|
|
|
форма. |
||||||||
12 |
Дана функция |
|
|
|
1. |
; |
|
|
|
||||||
|
|
x |
y |
f |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
0 |
1 |
|
2. |
; |
|
|
|
|||||
|
|
0 |
1 |
0 |
|
3. |
; |
|
|
|
|||||
|
|
1 |
0 |
0 |
|
|
|
|
|||||||
|
Её СДНФ |
1 |
1 |
0 |
|
4. |
; |
|
|
|
|||||
|
имеет вид … |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
5. |
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
Аббревиатура СКНФ расшифровывается |
|
1. Современная конечная |
||||||||||||
|
как … |
|
|
|
|
нормальная форма; |
|||||||||
|
|
|
|
|
|
2. |
Совершенная |
||||||||
|
|
|
|
|
|
|
конструктивная нормальная |
||||||||
|
|
|
|
|
|
|
функция; |
||||||||
|
|
|
|
|
|
|
3. |
Совершенная конъюнктивная |
|
||||||
|
|
|
|
|
|
|
нормальная форма; |
|
|
||||||
|
|
|
|
|
|
|
4. |
Совершенная краткая |
|||||||
|
|
|
|
|
|
|
нормальная форма; |
||||||||
|
|
|
|
|
|
5. |
Своевременная конечная |
||||||||
|
|
|
|
|
|
|
нормальная форма. |
||||||||

vk.com/club152685050 | vk.com/id446425943
|
|
|
|
|
|
|
1. |
0; |
|
|
|
||||
|
|
|
|
|
|
|
|
2. |
1; |
|
|
|
|
||
14 |
Импликация |
равна … |
|
3. |
x; |
|
|
|
|
||||||
4. |
; |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
5. . |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
0; |
|
|
|||||
|
|
|
|
|
|
|
|
2. |
|
x |
; |
|
|
|
|
15 |
Эквивалентность |
равна … |
|
3. |
|
1; |
|
|
|||||||
4. |
-1; |
|
|
||||||||||||
|
|
|
|
|
|
|
4. . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
0; |
|
|
|
||||
|
|
|
|
|
|
|
|
2. |
1; |
|
|
|
|
||
|
|
|
|
|
|
|
|
3. |
y; |
|
|
|
|||
16 |
Эквивалентность |
равна … |
4. |
; |
|
|
|
||||||||
|
|
|
|
|
|
|
5. . |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
Дана функция |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1. |
|
|
|
|
|
; |
|
||||
|
|
x |
|
y |
f |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
0 |
1 |
|
2. |
; |
|||||||
|
|
0 |
|
1 |
1 |
|
3. |
; |
|
||||||
|
|
1 |
|
0 |
0 |
|
|
||||||||
|
Её СКНФ |
1 |
|
1 |
1 |
|
4. |
; |
|
||||||
|
имеет вид … |
|
|
|
|||||||||||
|
|
|
|
|
|
|
5. |
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
Дизъюнкция |
|
|
|
1. 0; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2. |
1; |
|
|
|
|
|
|
|
при z = 1 равна … |
|
|
|
|
3. y; |
|
||||||||
|
|
|
|
|
|
|
4. |
x; |
|||||||
|
|
|
|
|
|
|
5. |
-1. |
|
|
|
||||
19 |
Дизъюнкция |
|
|
|
1. |
0; |
|
|
|
||||||
|
|
|
|
|
|
|
2. |
y; |
|||||||
|
равна … |
|
|
|
3. |
; |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
4. |
1; |
|
|
|
||||
|
|
|
|
|
|
|
|
5. |
-1. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
Конъюнкция |
|
|
|
1. |
x; |
|||||||||
|
|
|
|
|
|
|
|
2. |
0; |
|
|
|
|
||
|
равна … |
|
|
|
3. |
; |
|
|
|
||||||
|
|
|
|
|
|
|
4. |
1; |
|
|
|
||||
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
Отрицание конъюнкции |
|
|
1. |
x; |
||||||||||

vk.com/club152685050 | vk.com/id446425943
|
равно … |
2. |
; |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
1; |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
4. |
-1; |
|
|
|
|
|
|
|
|||
|
|
5. |
0. |
|
|
|
|
|
|
|
||||
22 |
Выражение |
1. |
0; |
|
|
|
|
|
|
|||||
|
|
2. |
|
β; |
||||||||||
|
равно … |
|
3. |
|
α; |
|
|
|
|
|
|
|||
|
4. |
1; |
||||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
5. . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
Дизъюнкция |
1. 0; |
|
|
|
|
|
|
|
|
||||
|
|
2. |
β; |
|||||||||||
|
равна … |
|
3. |
α; |
|
|
|
|
|
|
|
|||
|
4. |
1; |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
5. . |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
Формула |
1. |
; |
|||||||||||
|
|
|||||||||||||
|
равна … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
; |
|||||||||||
|
|
3. |
; |
|||||||||||
|
|
4. |
; |
|||||||||||
|
|
5. |
1. |
|
|
|
|
|||||||
25 |
Формула |
1. |
; |
|
|
|||||||||
|
|
|
|
|||||||||||
|
равна … |
2. |
; |
|
|
|||||||||
|
|
3. |
; |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4. |
; |
|
|
|||||||||
|
|
5. |
0. |
|
|
|
|
|||||||
26 |
Дана функция |
1. |
0; |
|
|
|
|
|
|
|||||
|
|
|
2. |
1; |
|
|
|
|
|
|
|
|||
|
Вычислить |
|
3. |
|
z; |
|
|
|||||||
|
. |
4. |
|
y; |
||||||||||
|
5. |
|
x. |
|||||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
Множество |
|
1. |
A |
; |
|
|
|||||||
|
|
|
2. |
B |
; |
|
|
|||||||
|
равно … |
|
3. U; |
|||||||||||
|
|
4. |
; |
|
|
|
|
|
|
|
||||
|
|
5. . |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
Для обозначения пустого множества |
1. |
|
∞; |
||||||||||
|
используется символ … |
2. |
; |
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
3. |
|
U; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
4. |
|
; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

vk.com/club152685050 | vk.com/id446425943
|
|
|
|
5. . |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
29 |
Если |
является элементом множества A, |
1. |
; |
|||||||
|
|||||||||||
|
то пишут … |
|
2. |
; |
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
3. |
; |
||||||
|
|
|
|
4. |
; |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
30 |
Пусть конечное множество A имеет |
1. |
; |
|
|
|
|
||||
|
мощность n. Тогда мощность его булеана |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равна … |
|
2. |
; |
|
|
||||
|
|
|
3. |
; |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
4. |
n; |
||||||
|
|
|
|
5. |
2n. |
||||||
31 |
В группе 8 мальчиков и 5 девочек. |
1. |
14; |
|
|
|
|
||||
|
Сколько можно составить различных пар |
2. |
6; |
|
|
|
|
||||
|
«мальчик, девочка»? |
3. |
5; |
|
|
|
|
||||
|
|
|
|
4. |
3; |
|
|
|
|
||
|
|
|
|
|
5. |
40. |
|
|
|
|
|
32 |
Бросаются 3 игральные кости. Сколько |
1. |
18; |
|
|
|
|
||||
|
исходов можно наблюдать. |
2. |
9; |
|
|
|
|
||||
|
|
|
|
3. |
36; |
|
|
|
|
||
|
|
|
|
4. |
72; |
|
|
|
|
||
|
|
|
|
|
5. |
216. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
33 |
Сколько существует различных способов |
1. |
5; |
|
|
|
|
||||
|
построения в шеренгу 5-ти человек? |
2. |
10; |
|
|
|
|
||||
|
|
|
|
3. |
25; |
|
|
|
|
||
|
|
|
|
|
4. |
120; |
|
|
|
|
|
|
|
|
|
|
5. |
250. |
|
|
|
|
|
34 |
Бросают три монеты достоинством: 1 |
1. |
3; |
|
|
|
|
||||
|
рубль, 2 рубля и 5 рублей. Сколько |
2. |
6; |
|
|
|
|
||||
|
различных исходов можно наблюдать? |
|
3. |
8; |
|
|
|
|
|||
|
|
|
|
|
4. |
16; |
|
|
|
|
|
|
|
|
|
5. |
32. |
|
|
|
|
||
35 |
Вычислите |
. |
1. |
100; |
|
|
|||||
|
2. |
98; |
|
|
|||||||
|
|
|
|
3. |
980; |
|
|
||||
|
|
|
|
|
4. |
1000; |
|
|
|||
|
|
|
|
|
5. |
9900. |
|
|
|||
36 |
В группе 10 студентов. Двоих надо |
1. |
10; |
|
|
||||||
|
отправить в деканат. Сколькими |
2. |
100; |
|
|
||||||
|
различными способами можно это |
3. |
8; |
|
|
||||||
|
сделать? |
|
|
4. |
45; |
|
|
|
|||
|
|
|
|
|
5. |
54. |
|
|
|
||
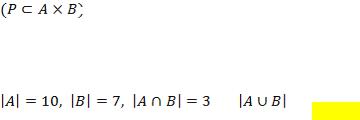
vk.com/club152685050 | vk.com/id446425943
37 |
Сколько пятизначных чисел можно |
1. |
15; |
|
|
|
|
|
|
|
|||||
|
записать, используя цифры 2,4 и 5? |
2. |
81; |
|
|
|
|
|
|
|
|||||
|
|
|
3. |
243; |
|
|
|
|
|
|
|
|
|||
|
|
|
4. |
1024; |
|
|
|
|
|
|
|
|
|||
|
|
5. |
6. |
|
|
|
|
|
|
|
|||||
38 |
Пусть A и B – множества, P – некоторое |
|
1. Прямым произведением; |
||||||||||||
|
подмножество их декартова произведения |
|
2. Унарным отношением; |
||||||||||||
|
. Тогда тройку (A, B, P) |
3. |
Простой триадой; |
||||||||||||
|
|
4. Сложной триадой; |
|||||||||||||
|
называют … |
|
5. |
Бинарным отношением. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39 |
Пусть A и B – некоторые множества, |
1. |
17; |
|
|
|
|
|
|
||||||
|
, то |
2. |
20; |
|
|
|
|
|
|
||||||
|
|
3. |
14; |
|
|
|
|
|
|
|
|
||||
|
составит … |
|
4. |
124; |
|
|
|
|
|
|
|||||
|
5. |
210. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
Какую алгебраическую структуру |
|
1. Полугруппа; |
|
|
|
|
|
|||||||
|
образуют множество натуральных чисел и |
|
2. Моноид; |
|
|
|
|
|
|||||||
|
операция сложения? |
|
3. Группа; |
||||||||||||
|
|
4. |
Абелева группа; |
||||||||||||
|
|
5. |
Полиноид. |
||||||||||||
41 |
Два ребра графа называются |
|
1. Они инцидентны одной и той |
||||||||||||
|
параллельными, если … |
|
же вершине; |
||||||||||||
|
|
|
2. |
Обе концевые вершины |
|
|
|||||||||
|
|
|
одного ребра совпадают с |
|
|
||||||||||
|
|
|
концевыми вершинами |
|
|
|
|
||||||||
|
|
|
другого; |
|
|
|
|
|
|||||||
|
|
|
3. |
Они не пересекаются; |
|||||||||||
|
|
4. |
Они входят в состав одного и |
||||||||||||
|
|
|
того же цикла; |
||||||||||||
|
|
5. |
Если они образуют две петли |
||||||||||||
|
|
|
к одной вершине. |
||||||||||||
42 |
Степенью вершины графа называется … |
|
1. Число смежных с ней |
||||||||||||
|
|
|
вершин; |
||||||||||||
|
|
2. |
Число связанных с ней |
||||||||||||
|
|
|
вершин; |
||||||||||||
|
|
|
3. |
Число инцидентных ей |
|
|
|||||||||
|
|
|
ребер; |
|
|
|
|
||||||||
|
|
|
4. |
Число циклов, в которые |
|||||||||||
|
|
|
входит вершина; |
||||||||||||
|
|
5. |
Вес максимального ребра, |
||||||||||||
|
|
|
инцидентного этой вершине. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
Степень висячей вершины графа равна … |
1. |
0; |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2. |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
3; |
|
|
|
|
|
|
|
|
|
|
||
|
|
5. |
-1. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44 |
Граф содержит эйлеров цикл тогда и |
|
1. Степени всех вершин четны; |
|
|||||||||||
|
только тогда, когда … |
|
2. Степени всех вершин равны |
|
|||||||||||
|
|
|
между собой; |
||||||||||||

vk.com/club152685050 | vk.com/id446425943
|
|
|
|
3. |
В графе нет изолированных |
|||||||||||
|
|
|
|
|
вершин; |
|||||||||||
|
|
|
|
4. |
Любые две вершины |
|||||||||||
|
|
|
|
|
являются смежными; |
|||||||||||
|
|
|
|
5. |
Степени всех вершин |
|||||||||||
|
|
|
|
|
нечётны. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
45 |
Граф называется эйлеровым, если … |
|
1. В нём существует замкнутая |
|
||||||||||||
|
|
|
|
|
цепь, содержащая все рёбра |
|
|
|||||||||
|
|
|
|
|
графа; |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2. |
Любые две вершины |
||||||||||
|
|
|
|
|
соединены некоторым ребром; |
|||||||||||
|
|
|
|
3. |
Каждому ребру приписан |
|||||||||||
|
|
|
|
|
некоторый вес; |
|||||||||||
|
|
|
|
4. |
Существует, по крайней |
|||||||||||
|
|
|
|
|
мере, одна изолированная |
|||||||||||
|
|
|
|
|
вершина. |
|||||||||||
|
|
|
|
5. |
Если веса всех его рёбер |
|||||||||||
|
|
|
|
|
положительны. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
46 |
Множество А называется счётным, если |
|
1. Эквивалентно множеству |
|||||||||||||
|
оно … |
|
|
|
комплексных чисел; |
|||||||||||
|
|
|
|
|
2. |
Эквивалентно множеству |
|
|||||||||
|
|
|
|
|
натуральных чисел; |
континууму |
||||||||||
|
|
|
|
|
3. |
Эквивалентно |
||||||||||
|
|
|
|
[0,1]; |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
4. |
Эквивалентно конечному |
|||||||||||
|
|
|
|
|
множеству мощности m; |
|||||||||||
|
|
|
|
5. |
Эквивалентно множеству |
|||||||||||
|
|
|
|
|
вещественных чисел. |
|||||||||||
47 |
Дан универсум |
|
1. |
, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
и его подмножества |
|
2. |
, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
3. |
|
|
|
|
|
, |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
и |
. |
4. |
;. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Найти |
. |
|
5. |
|
|
|
|
|
|
|
|
|
|||
48 |
Дана функция |
. Найти полный |
1. |
, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||
|
прообраз элемента 4, т.е. |
. |
2. |
, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
, |
|
|
|
|
|
|
||||
|
|
|
|
4. |
, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
5. . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
Дана функция |
. Найти образ |
1. |
[-4, 9]; |
|
|
|
|
|
|
|
|
||||
|
2. |
[ 4, 9]; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
vk.com/club152685050 | vk.com/id446425943
|
множества [-3, 3]. |
|
3. |
[ |
0, 9]; |
|
|
|
|
|
4. |
[ |
0, 4]; |
|
|
|
|
5. |
[ 2, 3]. |
|
|
||
50 |
Взаимно-однозначное отображение иначе |
|
1. Сюръективным; |
||||
|
называется … |
|
2. Инъективным; |
||||
|
|
3. |
Неособенным; |
||||
|
|
4. |
Субъективным; |
||||
|
|
|
5. |
Биективным. |
|
||
