Общая картография

vk.com/club152685050 | vk.com/id446425943

Таблица 1

Определение длины линии с помощью циркуля – измерителя

11

vk.com/club152685050 | vk.com/id446425943

Цена деления палетки по картографической таблице Данный объект расположен больше относительно меридиана, тогда

воспользуемся формулой:

Где Dп – длина отрезка параллели в 30’ по долготе, n – количество шагов. 1 участок раствор 2мм:

Dм (50°–55°) = (35848– 31998) *10= 38500 м = 38,5 км n =11

38500

d1 3,5км 11

Погрешность между 1 и 2 методами Так как длина реки, вычисленная 2 способом, оказалась ближе всего к

истинному значению длины реки, взятому из источников, то эту длину возьмем за эталон и посчитаем погрешность:

vk.com/club152685050 | vk.com/id446425943

III.Определение длины линии с помощью курвиметра

vk.com/club152685050 | vk.com/id446425943

60° и 65°

параллелями

Участок 50°

меридиана,

60° и 65°

параллелями

L 489,4 км

Погрешность между 2 и 3 методами Так как длина реки, вычисленная 2 способом, оказалась ближе всего к

истинному значению длины реки, взятому из источников, то эту длину возьмем за эталон и посчитаем погрешность:

При измерении длин извилистых линий с помощью циркуля-

измерителя фактически измеряется не сама извилистая линия, а ломаная,

получаемая при многократном отложении измерителем отрезков, равных размеру его раствора.

Вопросами изыскания надежных способов учета извилистости при измерении длин кривых линий по картам занимались многие исследователи

(А.А.Тилло, Н.М.Волков, Ю.М.Шокальский, А.К.Маловичко,

Г.И.Знаменщиков, Ю.С.Фролов и др.).

4.1. Метод Ю.М.Шокальского

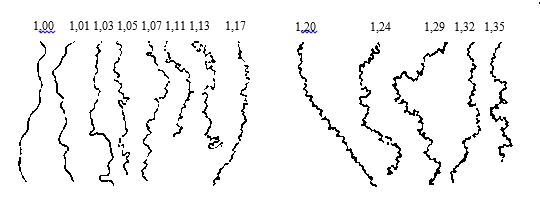
Измеряя некоторые реки азиатской части России циркулями с разными растворами, Ю.М.Шокальский построил графики зависимости полученных длин рек от размеров растворов циркулей-измерителей. Эти графики были использованы для получения поправок за извилистость, значения которых определялись визуально по особо составленной шкале извилистости.

14

vk.com/club152685050 | vk.com/id446425943

Рисунок 1. Образцы извилистых линий ГГИ. На кривых указаны значения коэффициентов извилистости

При измерении извилистых линий методом Ю.М.Шокальского линия разбивается на отдельные участки по степени их извилистости. Каждый участок измеряется специальным циркулем с постоянным раствором, равным

2,4 мм. Полученная длина линии по каждому участку умножается на поправочный коэффициент k , соответствующий извилистости измеряемого участка.

Таким образом, методом Ю.М.Шокальского длина извилистой линии может быть определена из выражения

n– число отложений циркуля в измеряемой линии.

4.1.1.Вычисления

l 497,5 км

4.2. Метод Н.М.Волкова

15

vk.com/club152685050 | vk.com/id446425943

Длина извилистой линии, измеряемой по карте данного масштаба,

возрастает по мере уменьшения раствора циркуля. Если отложить на графике по оси абсцисс значения d, а по оси ординат соответствующие им значения l,

то получим кривую, удовлетворяющую уравнению параболы. При уменьшении размера раствора, в пределе стремящегося к нулю, можно получить действительную, или приведенную, длину lпр линии с учетом всех ее извилин и изгибов.

Приведённая длина линии вычисляется по формуле:

n– число отложений циркуля в измеряемой линии.

1.2.1.Вычисления

l 512,3км

4.3.Метод А.К.Маловичко

Для определения аналитической зависимости между длинами линий l1

и l2 , полученными с использованием циркулей с растворами d1 и d 2 , и

приведенной длиной извилистой линии lпр используются правильные геометрические линии. А.К.Маловичко для определения lпр предложил аппроксимировать извилистые линии окружностями.

Тогда приведенная длина находится о формуле:

16

vk.com/club152685050 | vk.com/id446425943

l 556,8км

4.4. Метод Ю.С.Фролова

Дальнейшие изыскания в области определения аналитических зависимостей между длинами, полученными из измерений, и приведенными длинами для правильных геометрических линий привели к использованию для приведения линии, состоящей из сопряженных полуокружностей. В этом случае длина приведенной линии вычисляется по формуле:

4.4.1 Вычисления

t d2 d1 2; к 0,33

lпр1 24,5 0,33 24,5 19,2 26,25 км

lпр2 117,0 0,33 117,0 117,6 117,20 км lпр3 393,7 0,33 393,7 323,0 417,03км

l 560,48 км

17

vk.com/club152685050 | vk.com/id446425943

Вывод

В ходе выполненной лабораторной работы была определена длина линии, а

именно длина реки Вымь, протяженность которой равна 499 км. Данная работа проведена при помощи 7 методов. За эталон был взят метод:

определение длины при помощи циркуля-измерителя. Полученный результат равен 497,5 км, расхождение с истинным значением составило 0,3%.

Результаты, полученные из методов вероятностного, Шокальского, Волкова,

Маловичко, Фролова, значения которых 536,6 км, 497,5 км; 512,3 км; 556,8

км; 560,48 км; 489,4 км, соответственно, сравнивались с истинным значением реки. Полученные соотношения соответственно равны: 7,5%, 0,3%; 2,6%; 11,5%; 12,3%; 1,9%. Исходя из расчетов, можно сделать вывод, что самый неточный – метод Фролова, так как расхождение с истинным значением составило 12,3%.

18

vk.com/club152685050 | vk.com/id446425943

19

vk.com/club152685050 | vk.com/id446425943

1.Цель работы: научиться определять площади различных географических объектов различными способами на картах различного масштаба.

2.Оборудование: топографическая карта масштаба 1:10000,

палетка, картографические таблицы, циркуль – измеритель, масштабная линейка, планиметр.

3.Исходные данные:

Участки на карте масштаба 1:10 000 – лес Северный (рисунок 1),

Участок 2 (рисунок 2).

Участок на карте масштаба 1:5 000 000 – Италия (рисунок 3).

Площадь Италии – 301 338 км2.

Источник:http://geo.koltyrin.ru/country.php?country=%D0%98%D1%82% D0%B0%D0%BB%D0%B8%D1%8F [1].

4. Общие сведения: под определением площади участка по карте следует понимать совокупность вычислительных и измерительных работ, в

результате которых получают площади участков в натуре. При этом следует помнить, что измеряется участок не реальной физической поверхности, а

участок на поверхности эллипсоида. Точные определения площади можно получить только по топографическим картам. Однако на практике возникает необходимость получения приближенного значения на картах более мелкого масштаба.

20