Пучки и связки плоскостей.

Определение. Совокупность всех плоскостей, проходящих через одну и ту же прямую L, называется пучком плоскостей (с центром в L).

В полной аналогии с теоремой, относящейся к пучку прямых, доказывается следующее утверждение:

Если A₁x + B₁y+C₁z + D₁ = 0 и A₂x + B₂y+C₂z + D₂ = 0 уравнения двух различных не параллельных плоскостей, пересечением которых служит прямая L, а α и β — любые, не равные одновременно нулю числа, то

α(A₁x + B₁y+C₁z + D₁ ) + β (A₂x + B₂y+C₂z + D₂ ) = 0. (7.22)

есть уравнение плоскости, проходящей через прямую L. Более того, какова бы ни была наперед заданная проходящая через прямую L плоскость, она определяется уравнением (7.22) при некоторых α и β.

Доказательство этого утверждения аналогично доказательству теоремы для пучка прямых.

Сформулированное утверждение позволяет задавать прямую L, являющуюся линией пересечения двух не совпадающих и не параллельных плоскостей A₁x + B₁y+C₁z + D₁ = 0 и A₂x + B₂y+C₂z + D₂ = 0, не только двумя уравнениями этих плоскостей, но и любыми двумя различными уравнениями плоскости из пучка (7.22), полученными при каких угодно α и β.

Определение. Совокупность всех плоскостей, проходящих через данную точку M₀(x₀, y₀, z₀) называется связкой плоскостей (с центром в М₀).

Легко убедиться в том, что уравнение связки с центром в М₀(х₀, у₀, z₀) имеет вид

A(x-x₀) + B(y-y₀)+C(z-z₀) = 0, (7.23)

где А, В и С — какие угодно числа, не равные одновременно нулю.

В самом деле, всякая плоскость, определяемая уравнением (7.23), проходит через точку M₀(x₀, y₀, z₀). С другой стороны, если π — наперед заданная плоскость, проходящая через точку М₀(х₀, у₀, z₀), то эта плоскость однозначно определяется заданием, кроме точки M₀(x₀, y₀, z₀), еще нормального вектора n = (A, В, C) и потому определяется уравнением (7.7), совпадающим с уравнением (7.23).

Прямая линия в пространстве

Канонические уравнения прямой в пространстве. Прямую линию в пространстве, являющуюся линией пересечения двух различных не параллельных плоскостей, определяемых уравнениями A₁x + B₁y+C₁z + D₁=0 и A₂x + B₂y+C₂z + D₂=0), можно задавать либо двумя уравнениями этих плоскостей, либо двумя уравнениями пучка

α (A₁x + B₁y+C₁z + D₁ ) + β (A₂x + B₂y+C₂z + D₂ ) =0,

отвечающими произвольно взятым числам α и β.

При решении некоторых задач более удобным является специальный вид уравнения прямой в пространстве, к выводу которого мы и переходим.

Договоримся называть любой ненулевой вектор, параллельный данной прямой, направляющим вектором этой прямой.

Выведем уравнения прямой, проходящей через данную точку пространства М₁(х₁,у₁,z₁) и имеющей заданный направляющий вектор q = (l, m, n). Для этого заметим, что точка М(х, у, z) лежит на указанной прямой тогда и только тогда, когда векторы и q = (l, m, n) коллинеарны, т.е. тогда и только тогда, когда координаты этих векторов пропорциональны

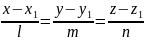(7.24)

Уравнения (7.24) есть искомые уравнения прямой, проходящей через точку М₁(х₁,у₁,z₁) и коллинеарной вектору q = (l, m, n). Эти уравнения принято называть каноническими уравнениями прямой. Заметим, что в канонических уравнениях (7.24) одно или два из чисел l, m и n могут оказаться равными нулю (все три числа l, m и n равняться нулю не могут, так как вектор q = (l, m, n) ненулевой). Так как всякую пропорцию мы договорились понимать как равенство 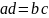, обращение в нуль одного из знаменателей в (7.24) означает обращение в нуль и соответствующего числителя. В самом деле, пусть, например, l=0, а n≠0 (хотя бы одно из трех чисел l, m и n не равно нулю). Тогда из пропорции

эквивалентной равенству 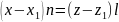заключаем, что

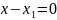
В заключение покажем, как прямую, заданную уравнениями двух различных не параллельных плоскостей

A₁x + B₁y+C₁z + D₁ = 0 , A₂x + B₂y+C₂z + D₂ = (7.25)

привести к каноническому виду (7.24). Достаточно найти: (1) хотя бы одну точку М₁(х₁,у₁,z₁), через которую проходит прямая (7.25); (2) направляющий вектор q = (l, m, n) прямой (7.25).

Начнем с нахождения координат х₁, у₁, z₁ точки М₁, через которую проходит прямая (5.52). Так как плоскости, определяемые уравнениями (5.52), не параллельны и не сливаются, то нарушается хотя бы одна из пропорции

.

Это означает, что хотя бы один из трех определителей второго порядка

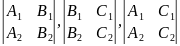
отличен от нуля. Пусть ради определенности отличен от нуля определитель 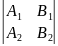. Тогда, взяв вместо z произвольное число z₁ и подставив его в уравнения (7.25), определим из системы (7.25) соответствующие этому z₁ значения х₁ и у₁:

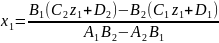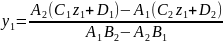, (7.26)

В частности, можно взять z₁ = 0. Тогда, воспользовавшись формулами (7.26), мы получим, что прямая (7.25) проходит через точку

.

Для нахождения координат l, m и n направленного вектора q прямой (7.25) заметим, что вектор q ортогонален каждому из нормальных векторов n₁ = (А₁, В₁, С₁) и n₂ = (А₂, В₂, С₂) плоскостей (7.25), так что можно положить вектор q = (l, m, n) равным векторному произведению [n_1,n₂]. Используя выражение векторного произведения в координатах, мы получим:

.

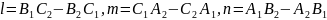Таким образом, для случая, когда отличен от нуля определитель 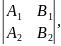канонические уравнения прямой (7.25) имеют вид

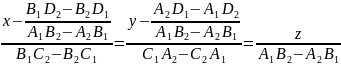
Аналогично записываются канонические уравнения прямой (5.52) для случая, когда отличен от нуля определитель

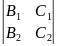или

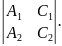
Уравнения прямой, проходящей через две различные точки М₁(х₁,у₁,z₁) и М₂(х₂,у₂,z₂). Эти уравнения имеют вид

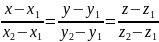
Для получения их достаточно заметить, что прямая проходит через точку М₁(х₁,у₁,z₁) и имеет направляющий вектор q = и воспользоваться каноническими уравнениями (7.24).

Параметрические уравнения прямой в пространстве. Параметрические уравнения прямой в пространстве элементарно получаются из канонических уравнений (7.24) этой прямой. Примем за параметр t каждое из отношений (7.24). Так как один из знаменателей (7.24) отличен от нуля, а соответствующий числитель может принимать какие угодно значения, то областью изменения параметра t является вся вещественная ось: -∞<t<+∞. Мы получим 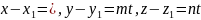, или окончательно

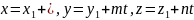(7.27)

Уравнения (7.27) и есть искомые параметрические уравнения прямой. Если принять параметр t за время, отсчитываемое от некоторого начального момента, то параметрические уравнения (7.27) определяют закон движения материальной точки по прямой линии с постоянной скоростью 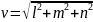(такое движение происходит по инерции).

Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых. Пусть две прямые в пространстве L₁ и L₂ заданы своими каноническими уравнениями

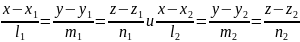
Тогда задача определения угла между этими прямыми сводится к определению угла φ между их направляющими векторами:

q₁ = (l₁, m₁, n₁) и q2 = (l₂, m₂, n₂).

Пользуясь определением скалярного произведения (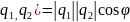 и выражением в координатах скалярного произведения и длин векторов q₁ и q₂, мы получим для определения угла φ следующую формулу:

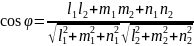(7.28)

Условие параллельности прямых L₁ и L₂, эквивалентное условию коллинеарности векторов q₁ и q₂, заключается в пропорциональности координат этих векторов, т.е. имеет вид

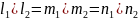(7.29)

Условие перпендикулярности прямых L₁ и L₂ получается из формулы (7.28) (при cosφ= 0) или выражается равенством нулю скалярного произведения (q_1,q₂). Оно имеет вид

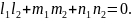(7.30)