Неполные уравнения плоскости. Уравнение плоскости в от­резках.

Определение. Общее уравнение плоскости (7.4) называется полным, если все его коэффициенты А, В, С и D отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, уравнение называется неполным.

Рассмотрим все возможные виды неполных уравнений:

1. D=0, уравнение 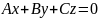определяет плоскость, проходящую через начало координат (поскольку координаты начала удовлетворяют этому уравнению).

2. A=0, уравнение определяет плоскость, параллельную оси Ох (поскольку нормальный вектор этой плоскости n = (0, В, C) перпендикулярен оси Ох).

3. B=0, уравнение определяет плоскость, параллельную оси Оу (ибо этой оси перпендикулярен нормальный вектор n = (А, 0, C)).

4. С=0, уравнение 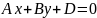определяет плоскость, параллельную оси Oz (ибо этой оси перпендикулярен нормальный вектор n = (А, В, 0)).

5. А=0, В=0, уравнение определяет плоскость, параллельную координатной плоскости Оху (ибо эта плоскость параллельна осям Ох и Оу).

6. А=0, С=0, уравнение 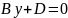определяет плоскость, параллельную координатной плоскости Oxz (ибо эта плоскость параллельна осям Ох и Oz).

7. B=0, С=0, уравнение 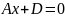определяет плоскость, параллельную координатной плоскости Oyz (ибо эта плоскость параллельна осям Оу и Oz).

8. А=0, В=0, D=0, уравнение определяет координатную плоскость Оху (ибо плоскость параллельна Оху и проходит через начало координат).

9) А=0, С=0, D=0, уравнение определяет координатную плоскость Oxz (ибо плоскость параллельна Oxz и проходит через начало координат).

10) B=0, С=0, D=0, уравнение определяет координатную плоскость Oyz (ибо плоскость параллельна Oyz и проходит через начало координат).

Рассмотрим теперь полное уравнение плоскости (7.4) и покажем, что оно может быть приведено к следующему виду:

(7.8)

называемому уравнением плоскости в отрезках.

В самом деле, так как все коэффициенты А, В, С и D отличны от нуля, мы можем переписать уравнение (7.4) в виде

и затем положить

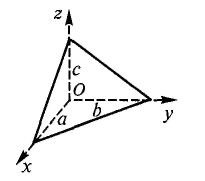
Замечание. Уравнении «в отрезках» (7.8) числа a, b и с имеют простой геометрический смысл: они равны величинам отрезков, которые отсекает плоскость на осях Ох, Оу и Oz соответственно (отрезки отсчитываются от начала ко­ординат, см. рис. ). Чтобы убедиться в этом, достаточно найти точки пересечения плоскости, определяемой уравнением (7.8), с осями координат.

Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей. Пусть две плоскости π₁ и π₂ заданы общими уравнениями A₁x + B₁y+C₁z + D₁ = 0 и A₂x + B₂y+C₂z + D₂ =0. Очевидно, вопрос об определении угла между указанными плоскостями сводится к определению угла φ между их нормальными векторами n₁ = (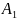 , , 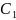) и n₂ = (А₂, В₂, С₂).

Из определения скалярного произведения и из выражения в координатах длин векторов n₁ и n₂ и их скалярного произведения, получим

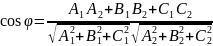(7.9)

Итак, угол φ между плоскостями π₁ и π₂ определяется с помощью формулы (7.9).

Условие параллельности плоскостей π₁ и π₂ эквивалентное условию коллинеарности векторов n₁ и n₂, заключается в пропор­циональности координат этих векторов, т.е. имеет вид

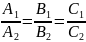(7.10)

Условие перпендикулярности плоскостей π₁ и π₂ может быть извлечено из формулы (7.9) (при cosφ = 0) или выражено равенством нулю скалярного произведения векторов n₁ и n₂. Оно имеет вид

А₁А₂ + В₁В₂+С₁С₂ = 0. (7.11)

Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой. Выведем уравнение плоскости, проходящей через три различные точки M₁(x₁,y₁,z₁), М₂(x₂,y₂,z₂) и M₃(х₃,у₃,z₃), не лежащие на одной прямой.

Так как указанные три точки не лежат на одной прямой, векторы 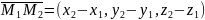и не коллинеарны, а поэтому точка M(x,y,z) лежит в одной плоскости с точками М₁, М₂ и М₃ тогда и только тогда, когда векторы , и компланарны, т.е. тогда и только тогда, когда смешанное произведение этих трех векторов равно нулю.

Используя выражение смешанного произведения в координатах, мы получим необходимое и достаточное условие принадлежности М(х, у, z) к указанной плоскости в виде

(7.12)

Уравнение первой степени (7.12) и является уравнением искомой плоскости.

Нормированное уравнение плоскости. Отклонение точки от плоскости. Рассмотрим плоскость π. Проведем через начало координат О прямую n, перпендикулярную плоскости π, и обозначим буквой Р точку пересечения прямой n и плоскости π (рис. 5.9). На прямой n возьмем единичный вектор n, направление которого совпадает с направлением отрезка ОР (в случае совпадения точек О и Р направление n выберем произвольно).

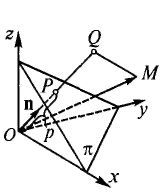
Выразим уравнение плоскости π через следующие параметры: длину р отрезка и углы α, β и γ наклона вектора n к осям Ох, Оу и Oz соответственно.

Так как n — единичный вектор, то его координаты, соответственно равные его проекциям на оси координат, имеют вид

n = {cos α, cosβ, cos γ}. (7.13)

Очевидно, точка М(х, у, z) лежит на рассматриваемой плоскости π тогда и только тогда, когда проекция вектора на ось, определяемую вектором n, равна р, т.е. при условии

(7.14)

Так как n — единичный вектор, то в силу определения скалярного произведения

(7.15)

Имея в виду, что = (х, у, z), а вектор n определяется равенством (7.13), мы получим следующее выражение для скалярного произведения этих векторов:

(7.16)

Из сопоставления (7.14), (7.15) и (7.16) следует, что точка М(х, у, z) лежит на плоскости π тогда и только тогда, когда координаты этой точки удовлетворяют уравнению

(7.17)

(7.17) и есть искомое уравнение плоскости π, выраженное через параметры р, α, β и γ. Это уравнение называется нормированным уравнением плоскости.

Введем теперь фундаментальное понятие отклонения произвольной точки М от данной плоскости π. Пусть число d обозначает расстояние от точки М до плоскости π.

Назовем отклонением δ точки М от плоскости π число +d в случае, когда точка М и начало координат О лежат по разные стороны от плоскости π, и число -d в случае, когда М и О лежат по одну сторону от π.

Если же начало координат О лежит на плоскости π, положим отклонение равным +d в случае, когда М лежит по ту сторону от π, куда направлен вектор n, и равным -d в противном случае.

Имеет место следующее важное утверждение.

Теорема 7.1. Левая часть нормированного уравнения плоскости (7.17) равна отклонению точки М с координатами х, у, z от плоскости π, определяемой уравнением (7.17).

Доказательство. Спроецируем точку М на ось, определяемую вектором n. Пусть Q — проекция точки М (см. рис.). Отклонение δ точки М от плоскости π равно PQ, где PQ обозначает величину направленного отрезка 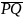оси, определяемой вектором n. Очевидно (см. рис.), что

(7.18)

Но 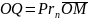, а последняя проекция в силу формул (7.15) и (7.16) равна

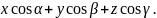
(7.19)

Сопоставляя формулы (7.18) и (7.19), получим .

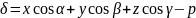Теорема доказана.

Теорема 7.1 приводит нас к следующему правилу: для нахождения отклонения δ точки M₀(x₀, y₀, z₀) от плоскости π следует в левую часть нормированного уравнения плоскости π подставить на место х, у и z координаты x₀, y₀ и z₀ точки М₀.

Разумеется, это правило позволяет отыскивать и расстояние от точки М до плоскости π, ибо расстояние равно модулю отклонения.

В заключение укажем алгоритм приведения общего уравнения плоскости (7.4) к нормированному виду (7.17). Так как указанное общее уравнение и уравнение (7.17) должны определять одну и ту же плоскость, то найдется число λ такое, что

(7.20)

Возводя в квадрат первые три равенства (5.47), складывая их и учитывая, что сумма квадратов направляющих косинусов равна единице, получим λ²(A² + B²+ C²) = 1, откуда

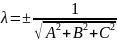(7.21)

Остается уточнить, какой из знаков ± следует взять в формуле (7.21). Так как по смыслу расстояние р всегда неотрицательно, то из последнего равенства (7.20) заключаем, что знак λ противоположен знаку D.

Итак, для приведения общего уравнения плоскости 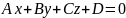к нормированному виду (7.17) следует умножить его на нормирующий множитель (7.21), знак которого противоположен знаку D.