Логарифмические частотные характеристики колебательного звена

Частотная передаточная функция колебательного звена имеет вид откуда при ; при .

Логарифмическая амплитудно-частотная функция имеет вид

1. низкочастотная асимптота имеет наклон 0 дБ/дек;

2. высокочастотная асимптота имеет наклон – 40дБ/дек.

3. обе асимптоты пересекаются на сопрягающей частоте.

При значениях 0,5 < x<1 характеристика близка к ломаной. Если же x<0,5, то получается заметный “горб”. Здесь необходимо вычислять превышение на частоте В упрощенных расчетах достаточно находить

Величина погрешности на сопрягающей частоте для различных x:

при x=1 DL=6,

x=0,5 DL=0,

x=0,1 DL=-14.

Если x от 1 до 0.3, то можно не строить точную ЛАЧХ, а доверитmся асимптотической.

Примеры колебательных звеньев: двигатели постоянного тока, LRC-цепи, регуляторы Уатта и др.

II. Интегрирующие звенья.

Идеальное интегрирующее звено.

Дифференциальное уравнение переходная функция передаточная функция

Дифференциальное уравнение может быть получено и в такой форме: проинтегрируем это уравнение и получим:

Выведем передаточную функцию:

- размерность передаточного коэффициента; в частном случае, когда входное воздействие и выходная функция имеют одинаковую размерность, [k]=c^-1.

Импульсная переходная характеристика:

Пример. Двигатель постоянного тока, выходная координата которого - угол поворота ротора a¶. Постоянную времени двигателя принять малой и не учитывать.

после интегрирования получим в форме изображений Лапласа

III. Дифференцирующие звенья.

1. Идеальное дифференцирующее звено.

Дифференциальное уравнение определим передаточную функцию

Дифференциальное уравнение записывают и в такой форме:

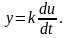
Пример. Тахогенератор- генератор постоянного или переменного тока, предназначенный для измерения скорости вращения механизмов.

Стат. характ. ТГ Стат. характ. ТГ

пост. тока. перем. тока.

Тахогенератором пост. тока свойственны пульсации из-за коллектора.

Высокий уровень помех и у тахогенераторов переменного тока.

Если пренебречь инерционностью тахогенератора, то, считая входом угол поворота вала, выходом напряжение, тахогенератор можно считать идеальным дифференцирующим звеном.

Пусть измерительным устройством (датчиком скорости) в проектируемой системе является тахогенератор постоянного тока (рис.1.)

П ри использовании ТГ в качестве датчика угловой скорости 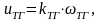в качестве преобразователя угла поворота

Рис. 1.

- конденсатор; если u_c – вход, i_c – выход, то 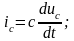конденсатор – идеальное дифференцирующее звено.

2. Форсирующее звено.

Дифференциальное уравнение переходная функция передаточная функция

ЛЧХ

w=1/T

Q(w)

L (w)

+20

+90°

20lgk

w, с^-1

Q, град

L, дБ

+45°

Пример. ПД-регудятор.