
mat
.docx
35. Производная обратной функции. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у0 имеет производную g '(v0), отличную от нуля, то в соответствующей точке x0=g(x0) функция y=f(x) имеет производную f '(x0), равную , т.е. справедлива формула . Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0. Покажем, что . Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. . Следовательно, , что и требовалось доказать. Эту формулу можно записать в виде .
|
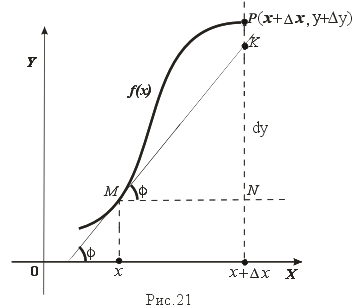
36. Геометрический смысл производной и дифференциала. Геометрический смысл производной Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение D x№ 0, причем x+D x О (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+D x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+D x,f(x+D x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОX через f (D x). Определение 3. Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при D x® 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика.
Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел limD x® 0f (D x) = f 0, который равен углу, образованному касательной с положительным направлением оси OX. Справедливо утверждение: Предложение 1. Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке M( x,f(x)) , причем угловой коэффициент этой касательной равен производной f'(x). Из этого утверждения вытекает геометрический смысл производной: производная f'(x0) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x0, который в свою очередь равен tg угла наклона касательной к графику функции. Тогда уравнение касательной к кривой f(x) в точке x0 имеет вид y
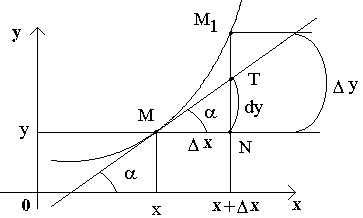
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА Рассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δx, тогда функция получит приращение Δy = NM1. Значениям x+Δx и y+Δy на кривой y = f(x) будет соответствовать точка M1(x+Δx; y+Δy). Из ΔMNT находим NT=MN·tg α. Т.к. tg α = f '(x), а MN = Δx, то NT = f '(x)·Δx. Но по определению дифференциала dy=f '(x)·Δx, поэтому dy = NT. Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х.
|
37. Производные основных элементарных функций. y = xn. Если n – целое положительное число, то, используя формулу бинома Ньютона: (a + b)n = an+n·an-1·b + 1/2∙n(n – 1)an-2∙b2+ 1/(2∙3)∙n(n – 1)(n – 2)an-3b3+…+ bn, можно
доказать, что
Итак, если x получает приращение Δx, то f(x+Δx) = (x + Δx)n, и, следовательно, Δy=(x+Δx)n – xn =n·xn-1·Δx + 1/2·n·(n–1)·xn-2·Δx2 +…+Δxn. Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3.
Найдем
предел Мы доказали эту формулу для n Î N. Далее увидим, что она справедлива и при любом n Î R. y= sin x. Вновь воспользуемся определением производной. Так как, f(x+Δx)=sin(x+Δx), то
Т Аналогично
можно показать, что
Рассмотрим функцию y= ln x. Имеем f(x+Δx)=ln(x+Δx). Поэтому
Итак,
Используя
свойства логарифма можно показать,
что
|
38. Производные высших порядков. Правила вычисления, правило Лейбница. Пусть функция y=f(x) дифференцируема на некотором отрезке [a; b]. Значение производной f'(x), вообще говоря, зависит от x, т.е. производная f'(x) представляет собой тоже функцию переменной x. Пусть эта функция также имеет производную. Дифференцируя ее, получим так называемую вторую производную от функции f(x). Производная от первой производной называется производной второго порядка или второй производной от данной функции y=f(x) и обозначается y''или f''(x). Итак, y'' = (y')'. Например, если у = х5, то y'= 5x4, а y''= 20x4. Аналогично, в свою очередь, производную второго порядка тоже можно дифференцировать. Производная от второй производной называется производной третьего порядка или третьей производной и обозначается y'''или f'''(x). Вообще, производной n-го порядка от функции f(x) называется производная (первая) от производной (n – 1)-го порядка и обозначается символом y(n) или f(n)(x): y(n) = (y(n-1))'.
|
40. Дифференцирование параметрически заданных функций.
|
41. Дифференциалы высших порядков. Нарушение инвариантности формы. Пусть имеем функцию y=f(x), где x – независимая переменная. Тогда дифференциал этой функции dy=f'(x)dx также зависит от переменной x, причем от x зависит только первый сомножитель f'(x) , а dx = Δx от x не зависит (приращение в данной точке x можно выбирать независимо от этой точки). Рассматривая dy как функцию x, мы можем найти дифференциал этой функции. Дифференциал от дифференциала данной функции y=f(x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y: d(dy)=d2y. Найдем выражение второго дифференциала. Т.к. dx от x не зависит, то при нахождении производной его можно считать постоянным, поэтому d2y = d(dy) = d[f '(x)dx)] = [f '(x)dx]'dx = f ''(x)dx·dx = f ''(x)(dx)2. Принято записывать (dx)2 = dx2. Итак, d2у= f''(x)dx2. Аналогично третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала: d3y=d(d2y)=[f ''(x)dx2]'dx=f '''(x)dx3. Вообще дифференциалом n-го порядка называется первый дифференциал от дифференциала (n – 1)-го порядка: dn(y)=d(dn-1y) dny = f (n)(x)dxn Отсюда, пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:
Неинвариантность дифференциалов высшего порядка При
Для
доказательства неинвариантности
дифференциалов высшего порядка
достаточно привести пример.
При n
= 2 и если
—
независимая переменная, то если
при
этом, С
учётом зависимости
|
42. Теорема Ферма
|
43. Теорема Ролля
|
44. Формула конечных приращений Лагранжа. Формула
конечных приращений
или теорема
Лагра́нжа о среднем значении
утверждает, что если функция f
непрерывна на отрезке [a;b]
и дифференцируема в интервале (a;b),
то найдётся такая точка
Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка. Механическое
истолкование:
Пусть f(t) —
расстояние точки в момент t
от начального положения. Тогда f(b)
− f(a)
есть путь, пройденный с момента t
= a
до момента t
= b,
отношение
Доказательство Для функции одной переменной: Введем
функцию
что и требовалось доказать. |
45. Теорема Коши. Пусть
даны две функции
и
определены
и непрерывны на отрезке
производные
производные и не обращаются в нуль одновременно на интервале
тогда
Доказательство Для
доказательства введём функцию Для
неё выполнены условия теоремы Ролля:
на концах отрезка её значения равны
f(a).
Воспользовавшись упомянутой теоремой,
получим, что существует точка c,
в которой производная функции F
равна нулю, а
|
46. Правило Лопиталя раскрытия неопределенности 0/0 Точная формулировка Условия:
и
дифференцируемы в проколотой окрестности
существует
тогда
существует
Пределы также могут быть односторонними. Отношение бесконечно малых Докажем
теорему для случая, когда пределы
функций равны нулю (то есть неопределённость
вида
Поскольку
мы рассматриваем функции f
и g
только в правой проколотой полуокрестности
точки a,
мы можем непрерывным образом их
доопределить в этой точке: пусть f(a)
= g(a)
= 0. Возьмём
некоторый x
из рассматриваемой полуокрестности
и применим к отрезку
но
f(a)
= g(a)
= 0, поэтому
Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим:
что является определением предела отношения функций.
|
47. Правило Лопиталя для раскрытия неопределенности ∞/∞ Точная формулировка Условия: или ; и дифференцируемы в проколотой окрестности ; в проколотой окрестности ; существует , Докажем
теорему для неопределённостей вида
Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие:
Зафиксируем
t
из отрезка
Для x, достаточно близких к a, выражение имеет смысл; предел первого множителя правой части равен единице (так как f(t) и g(t) — константы, а f(x) и g(x) стремятся к бесконечности). Значит, этот множитель равен 1 + β, где β — бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение ε, что и в определении для α:
Получили,
что отношение функций представимо в
виде (1
+ β)(A
+ α), и
Если же предел A бесконечен (допустим, он равен плюс бесконечности), то
В
определении β
будем брать
|
4 Пусть
Остаточный член в форме Пеано: В форме Пеано:
Доказательство. Утверждение теоремы означает, что существует П
Применим
к этому пределу правило Лопиталя,
повторив этот приём
|
51. Условия монотонности функции.
|
52. Экстремум функции. Необходимое условие экстремума. Пусть
дана функция
x0
называется точкой локального максимума
функции f,
если существует проколотая окрестность
x0 называется точкой локального минимума функции f, если существует проколотая окрестность такая, что
Если неравенства выше строгие, то x0 называется точкой строгого локального максимума или минимума соответственно. x0 называется точкой абсолютного (глобального) максимума, если
x0 называется точкой абсолютного минимума, если
Значение функции f(x0) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума. Следующая теорема даёт необходимое условие того, чтобы точка была точкой локального экстремума функции . Теорема
7.4
Если точка
--
это точка локального экстремума
функции
,
определенной в некоторой окрестности
точки х0, и существует производная в
этой точке
Доказательство этой теоремы сразу же следует из теоремы Ферма (см. гл. 5). Утверждение теоремы можно переформулировать так: если функция имеет локальный экстремум в точке , то либо 1) , либо 2) производная не существует. Точка называется критической точкой функции , если непрерывна в этой точке и либо , либо не существует. В первом случае (то есть при ) точка называется также стационарной точкой функции . Итак, локальный экстремум функции может наблюдаться лишь в одной из критических точек этой функции.
|
54. Достаточное условие экстремума, использующее высшие производные.
Пусть
--
стационарная точка функции
,
и в этой точке существует вторая
производная
Доказательство.
Поскольку
Пусть
.
Тогда из существования предела следует,
что для любого
при
Доказательство для случая совершенно аналогично.
|
55,56. Условия выпуклости и точки перегиба графика функции. Точка
перегиба функции
Необходимое
условие существования точки перегиба:
если функция f(x), дважды дифференцируемая
в некоторой окрестности точки x0,
имеет в x0
точку перегиба, то
Первое
достаточное условие существования
точки перегиба:
если функция f(x)
в некоторой окрестности точки x
k
раз непрерывно дифференцируема, причем
k
нечётно и
Второе достаточное условие существования точки перегиба: Если в некоторой точке вторая производная функции равна нулю, а третья не равна нулю, то эта точка является точкой перегиба.
56. Вертикальные и наклонные асимптоты. Асимптотой
графика функции
Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если выполнено хотя бы одно из условий
Прямая
y = b
называется горизонтальной
асимптотой
графика функции f (x)
при x → +∞,
если
Прямая
y = kx + b,
k ≠ 0
называется наклонной
асимптотой
графика функции f (x)
при x → +∞,
если
Для того, чтобы прямая y = kx + b была асимптотой графика функции y = f (x) при x → +∞, необходимо и достаточно, чтобы существовали конечные пределы
|
53. Достаточное условие экстремума, использующее первую производную. Пусть
в точке
Доказательство.
Пусть
По
теореме Лагранжа
Таким
образом доказано, что
Доказательство теоремы для точки минимума проводится аналогично. Теорема доказана. Если при переходе через точку производная не меняет знак, то в точке экстремума нет.
|

 = f(x0)+f'(x0)(x-x0)
= f(x0)+f'(x0)(x-x0)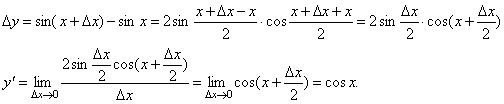 аким
образом,
аким
образом,
 Таким
образом, для нахождения производной
высшего порядка от данной функции
последовательно находят все ее
производные низших порядков.
Таким
образом, для нахождения производной
высшего порядка от данной функции
последовательно находят все ее
производные низших порядков.


 8.
Локальная формула Тейлора. Остаточный
член в форме Пеано.
8.
Локальная формула Тейлора. Остаточный
член в форме Пеано. ри
ри