
mat
.docx
Действительные числа
1. Действительные числа и их свойства. Принцип Архимеда.
2. Множество действительных чисел как метрическое пространство. Открытые и замкнутые множества в нем.
Леммы, связанные с полнотой множества действительных чисел:
3. Лемма о вложенных отрезках (принцип Коши - Кантора).
4. Лемма о конечном покрытии (принцип Бореля - Лебега).
5. Лемма о предельной точке (принцип Больцано - Вейерштрасса).
6. Г рани числовых множеств. Теорема существования точных граней.
Предел
7. Предел последовательности. Общие свойства предела.
8. Арифметические свойства сходящихся последовательностей. Предельный переход в неравенствах.
9. Бесконечно малые и бесконечно большие последовательности, их свойства.
10. Критерий сходимости монотонной последовательности. Число е.
11. Подпоследовательности. Теорема Больцано- Вейерштрасса.
12. Верхний и нижний пределы последовательностей.
13. Критерий Коши сходимости последовательностей.
14. Предел функции. Эквивалентность определений Гейне и Коши.
15. Свойства предела функции. Предельный переход и арифметические операции. Предельный переход и неравенства.
16. Предел сложной функции.
17. Предел по базе. Односторонние пределы, пределы на бесконечности.
18. Критерий Коши существования предела функции.
19. Замечательные пределы.
20. Существование предела монотонной функции.
21. Бесконечно малые и бесконечно большие функции. Сравнение асимптотического поведения функций. «О-о» символика.
Непрерывность
22. Непрерывность функции в точке. Точки разрыва, их классификация.
23. Непрерывность сложной функции. Арифметические свойства непрерывных функций.
Свойства функций, непрерывных на отрезке:
24. Теорема Вейерштрасса.
25. Теорема Кольцано - Коши.
26. Критерий непрерывности монотонной функции.
27. Теорема об обратной функции.
28. Равномерная непрерывность. Теорема Кантора.
29. Непрерывность основных элементарных функций.
Производная и дифференциал
30. Производная функции. Связь между существованием производной и непрерывностью.
31. Дифференциал. Необходимые и достаточные условия диффсрснцируемости.
32. Инвариантность формы первого дифференциала.
33. Правила дифференцирования.
34. Производная сложной функции.
35. Производная обратной функции.
36. геометрический смысл производной и дифференциала.
37. Производные основных элементарных функций.
38. Производные высших порядков. Правила вычисления, формула Лейбница.
39. Производные высших порядков от сложных и обратных функций.
40. Дифференцирование параметрически заданных функций.
41. Дифференциалы высших порядков. Нарушение инвариантности формы. Теоремы о среднем:
42. Теорема Ферма.
43. Теорема Ролля.
44. Формула конечных приращений Лагранжа.
45. Теорема Коши.
46. Правило Лопиталя раскрытия неопределенности 0/0.
47. Правило Лопиталя раскрытия неопределенности 8/8.
48. Локальная формула Тейлора. Остаточный член в форме Пеано.
49. Формула Тейлора с остаточным членом в форме Лагранжа и Коши.
50. Основные разложения по формуле Тейлора.
Применение дифференциального исчисления к задачам исследования поведения функций:
51. Условия монотонности функций.
52. Экстремум функции. Необходимое условие экстремума.
53. Достаточное условие экстремума, использующее первую производную.
54. Достаточное условие экстремума, использующее высшие производные.
55. Условия выпуклости и наличия точки перегиба графика функции.
56. Вертикальные и наклонные асимптоты.
17. Односторонние пределы. Пределы на бесконечности.
(Гейне):
Функция f
имеет в точке x0
предел слева
(справа),
если существует такое число
(Коши): Функция f имеет в точке x0 предел слева (справа), если
Число A называем пределом слева (справа) функции f в точке x0 и обозначаем f(x0 - 0) (f(x0 + 0)) или Функция f имеет предел в точке x0 тогда и только тогда, когда в этой точке существуют и равные между собой пределы слева и справа.
Предел функции на бесконечности в математическом анализе описывает поведение значения данной функции, когда её аргумент становится бесконечно большим по модулю. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < e. Запись этого факта:
Если область определения данной функции неограниченна снизу, то число b называется пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < e. Записывается это так:
|
18. Критерий Коши существования предела функции.
Условие Коши. Будем говорить, что функция f(x) удовлетворяет в точке a условию Коши, если для любого положительного числа e найдется положительное d(e), что для любых x1,x2, удовлетворяющих условию 0<|x1-a|<d, 0<|x2-a|<d, справедливо неравенство |f(x1-f(x2)|<e. Критерий Коши. Для того, чтобы существовал предел функции f(x) в точке a (limx ->af(x) = A ) необходимо и достаточно, чтобы f(x) удовлетворяла в точке a условию Коши. Доказательство Необходимость.
Пусть
Достаточность
Теорема
об эквивалентности двух определений
предела:
Применяем критерий Коши для последовательности. Докажем,
что этот предел не зависит от выбора
последовательности
не имеет предела, т.к. ее четные и нечетные члены сходятся к разным пределам A и B соответственно. Таким образом, получилось противоречие.
|
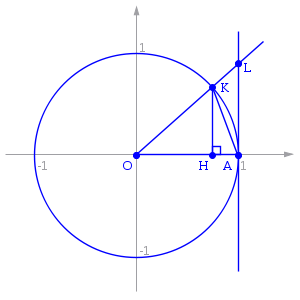
19. Замечательные пределы. Первый замечательный предел
Доказательство
Рассмотрим
односторонние пределы
Пусть
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX. Очевидно, что:
(где SsectOKA — площадь сектора OKA)
(из
Подставляя в (1), получим:
Так как при:
Умножаем на sinx:
Перейдём к пределу:
Найдём левый односторонний предел:
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1
Второй замечательный предел
Доказательство Для любого действительного положительного аргумента можно указать два последовательных натуральных числа, для которых будет выполнено неравенство n < x < n + 1. В том случае имеем n → ∞ ⇒ x → ∞. По свойству для неравенств имеем
Прибавим ко всем частям неравенств единицу
По свойству степеней имеем
Так как
и
то по теореме о пределе промежуточной функции имеем также и , что и требовалось доказать. Для отрицательного х доказательство аналогично.
|
|||
20. Существование предела монотонной функции. Функция
-
монотонно возрастающей, если из
-строго
монотонно возрастающей, если из
-
монотонно убывающей, если из
-строго
монотонно убывающей, если из
Если же для любых точек x1ÎX и x2ÎX, x1 < x2, выполняется неравенство f(x1)£f(x2) (соответственно неравенство f(x1) ³ f(x2)), то функцию называют неубывающей (невозрастающей). Иногда удобнее и в этом случае называть функцию возрастающей (убывающей) – но в широком смысле. Возрастающие и убывающие на множестве X функции называются монотонными на этом множестве. Теорема.
Пусть функция
Аналогично,
если функция f ограничена снизу, то в
точке a у неё существует конечный
предел справа, а если f не ограничена
снизу, то
Подобные утверждения справедливы и для убывающих функций; их можно получить, перейдя от функции f к функции –f. Доказательство.
Из ограниченности f следует существование
конечной точной верхней грани
Пусть теперь неубывающая функция f не ограничена сверху. Тогда для любого M существует такое, что M < f(x1), и вследствие того, что f не убывает на X, а это и говорит о том, что .
|
21. Бесконечно малые и бесконечно большие функции. Сравнение асимптотического поведения функций. «О-о» символика. Функция
y=f(x)
называется бесконечно
малой при x→a
или при x→∞,
если
функция, предел которой в данной точке равен нулю. Примеры. Функция
f(x)=(x-1)2
является бесконечно малой при x→1,
так как
Функция f(x) = tgx – бесконечно малая при x→0. f(x) = ln (1+x)– бесконечно малая при x→0. f(x) = 1/x– бесконечно малая при x→∞. Если
для любой последовательности
«O» большое и «o» малое (O и o) — математические обозначения для сравнения асимптотического поведения функций. Пусть f(x) и g(x) — две функции, определенные в некоторой проколотой окрестности точки x0, причем в этой окрестности g не обращается в ноль. Говорят, что: f
является «O» большим от g
при
f
является «о» малым от g
при
,
если для любого ε > 0 найдется такая
проколотая окрестность
Иначе говоря, в первом случае отношение | f | / | g | в окрестности точки x0 ограничено сверху, а во втором оно стремится к нулю при . Сравнение асимптотического поведения функций Определение.
Говорят, что функция
Замечание.
Если функция
Замечание.
Если
в некоторой
|
22. Непрерывность функции в точке. Точки разрыва, их классификация. Определение 1: Пусть
f(x)
определена в некоторой окрестности
точки а. f(x)
называется непрерывной в точке а если
Определение 2: f(x) называется непрерывной в точке а, если > 0 > 0: | f(x) - f(а) | < при | х - а | < . f(x) = f(а) Таким образом, можно сказать, что функция непрерывна в точкеx0, если выполнены 3 условия: 1-она определена в точке x0 и в некоторой её окрестности; 2-имеет предел при x → x0; 3-этот предел равен значению функции в точке x0. Предельные точки области определения функции, в которых эта функция не является непрерывной, называются точками её разрыва. Классификация точек разрыва: 1) 2)
-
т.р. 1-го
рода: К
примеру,
3)
-
т.р. 2-го рода: все остальные т.р.,
например, точки бесконечного разрыва.
В частности,
|
|||
23. Непрерывность сложной функции. Арифметические свойства непрерывных функций.
Пусть аргумент t функции y = f(t) является функцией аргумента x: t = (x). В этом случае говорят, что переменная у является сложной функцией от аргумента х или у является суперпозицией функций f и . y = f( (x)). Пример: y
= sin( y = sin t, где t = .
Если
f(x)
и g(x)
непрерывны в точке а, то f(x)
g(x),
f(x)g(x)
и
Доказательство: По условию f(x) = f(а), g(x) = g(а) [ f(x) + g(x)] = f(a) + g(а). а это и означает непрерывность суммы функций в точке а. Точно также доказывается непрерывность разности, произведения, частного. Теорема доказана.
|
24. Теорема Вейерштрасса. Первая теорема Вейерштрасса. Пусть
Доказательство: Докажем,
что
Предположим
противное,
то есть
Получим
1)
2)
Из
этих определений получаем
=>
-подпоследовательность
последовательности
:
=>
Вторая теорема Вейерштрасса. Пусть
.
Тогда
Замечание: Непрерывная на отрезке функция на этом отрезке достигает своего наибольшего и наименьшего значения, причем в условиях теоремы отрезок по существу. Доказательство: По
условию теоремы
=>
ограничена
на
=>
|
25. Теорема Больцано-Коши. Пусть
дана непрерывная функция на отрезке
Доказательство Рассмотрим
функцию
Обозначив
полученный отрезок
Пусть
-
общая точка всех отрезков
,
g(c) = lim g(an) = lim g(bn). Поскольку
получим, что
|
|||
26. Критерий непрерывности монотонной функции.
Для того, чтобы монотонная функция f(x) определенная на [a,b] была непрерывна на [a,b] необходимо и достаточно, чтобы множество значений f(x) заполняло целиком отрезок с концами f(a), f(b) (либо[f(a), f(b)] либо [f(b), f(a)]).
Доказательство. Лемма.
Для монотонно
возрастающей на данном отрезке функции
существуют:
Доказательство
леммы. Положим
для некоторого
x0(a,b],
A=
Так как функция монотонно возрастает, то x(x,x0):A- < f(x) f(x)A. Таким образом, равенство доказано. Аналогично для предела справа . Для монотонно убывающей функции справедливо аналогичное утверждение. Следствие 1. Монотонно убывающая (возрастающая) на [a,b] функция имеет конечные односторонние пределы. Следствие 2. Монотонно убывающая (возрастающая) на [a,b] функция может иметь там лишь разрывы первого рода. Доказательство критерия. Функцию будем предполагать монотонно возрастающей. Необходимость уже была доказана ранее (пункт 4, следствие 2). Достаточность. Предположим противное. В точке x0 имеется разрыв. Этот разрыв обязан быть разрывом первого рода и, следовательно, должно нарушаться одно из двух соотношений:
Пусть,
например,
Имеем
Аналогично проводится доказательство в случае существования разрыва слева. Замечание. Для монотонно убывающей функции доказательство проводится заменой f на –f.
|
27. Теорема об обратной функции. если функция f:X→Y , где Y=f(X), обратима, то для нее существует единственная обратная функция f−1:Y→X и если y=f(x) то x=f−1(y), и если x=f−1(y), то y=f(x) и f−1(f(x))=x при любом x∈X , f−1(f(y))=y при любом y∈Y . Доказательство. Положим для определенности, что функция f возрастающая. Обратимость функции f — очевидное следствие теоремы о корне (Пусть функция f возрастает (или убывает) на промежутке I, число а - любое из значений, принимаемых f на этом промежутке. Тогда уравнение f(x)=a имеет единственный корень на этом промежутке I.)
. Поэтому остается доказать, что функция g, обратная к f, возрастает на множестве E(f). Пусть x1 и x2 — произвольные значения из Е (f), такие, что x2> x1. и пусть y1=g(x1), y2=g(x2). По определению обратной функции x1=f(y1) и x2=f(y2). Воспользовавшись тем условием, что f — возрастающая функция, находим, что допущение y1 ≥ y2 приводит к выводу f (y1)≥f(y2), т. е. x1≥ x2. Это противоречит предположению x2> x1. Поэтому y2> y1 , т. е. из условия x2> x1 следует, что g (x2)>g (x1). Именно это и требовалось доказать.
|
28, 32. Инвариантность формы первого дифференциала. 28. Равномерная непрерывность. Теорема Кантора.
Функция f: X → R называется равномерно-непрерывной на
множестве X,
если Теорема Кантора Если функция f: [a, b] → R непрерывна на сегменте [a, b], то она равномерно-непрерывна на этом сегменте.
32. Инвариантность формы первого дифференциала. Инвариантность формы первого дифференциала Пусть y = f ( u ( x )) является сложной функцией аргумента x. По определению дифференциала функции имеем df = f '(x)·u '(x)·dx. Так как, в свою очередь, du = u '(x)· dx, то из последнего соотношения получим df = f '(u)·du. Что совпадает с соотношением dy = f '(x)·dx. Форма дифференциала первого порядка сохраняется вне зависимости от того, является ли аргумент независимым или является в свою очередь функцией другого аргумента.
|
|||
29. Непрерывность основных элементарных функций. Все элементарные функции являются непрерывными в любой точке своей области определения. Функция называется элементарной, если она построена из конечного числа композиций и комбинаций (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя: Алгебраические многочлены
Рациональные дроби
Степенные
функции
Показательные
функции
Логарифмические функции
Тригонометрические функции
Обратные
тригонометрические функции
Гиперболические функции
|
30. Производная функции. Связь между производной и непрерывностью. Пусть
в некоторой окрестности точки
f(x0 + h) = f(x0) + Ah + o(h) если существует. Определение производной функции через предел Пусть в некоторой окрестности точки определена функция Производной функции f в точке x0 называется предел, если он существует,
Общепринятые обозначения производной функции y = f(x) в точке x0
|
31. Дифференциал. Необходимые и достаточные условия дифференцируемости. Дифференциа́л — линейная часть приращения функции. Для функций Дифференциал
функции
где f'(x0) обозначает производную f в точке x0. Таким
образом df
есть функция двух аргументов
Дифференциал
может быть определён напрямую, т.е.,
без привлечения определения производной
как функция
Теорема: Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке. При этом
где α(Δx) - бесконечно малая функция, при Δx→0. Доказательство Необходимость. Предположим: функция дифференцируема в точке x0, т.е. Δy=A·Δx+α(Δx)·Δx. Разделив обе части данного равенства на Δx, получим: ΔxΔy=A+α(Δx). Из определения производной функции в точке: y/(x0)=limΔx→0ΔxΔy=limΔx→0(A+α(Δx))=A. Т.е. получили, что существует конечная производная функции в точке x0 и y/(x0)=A. Достаточность. Пусть существует конечная производная y/(x0)∈R . Покажем дифференцируемость функции. y/(x0)=limΔx→0ΔxΔy. Если функция f(x) имеет конечный предел b при Δx→0 , то ее можно представить: f(x)=b+α(x) (α(x)→0) . Исходя из этого: ΔxΔy=y/(x0)+α(Δx), где limΔx→0α(Δx)=0, Δy=y/(x0)·Δx+α(Δx)·Δx→ A=y/(x0) . Теорема доказана.
|
|||
33. Правила дифференцирования. При
дифференцировании константу можно
выносить за производную:
|
34. Производная сложной функции. Если
функция u=
u(x)
имеет в некоторой точке x0
производную
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x. Доказательство. При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx: Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0). Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0. По
условию
где α→0 при Δu→0, а, следовательно, и при Δx→0. Перепишем это равенство в виде: Δy= y 'uΔu+α·Δu. Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx
По
условию
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной. Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y 'x осуществляется последовательным применением предыдущей теоремы. По
доказанному правилу имеем y
'x=
y
'u·u
'x
. Применяя эту же теорему для u
'x
получаем
y 'x = y 'x· u 'v· v 'x = f 'u (u)·u 'v (v)·v 'x (x).
|
35. Производная обратной функции. Если
для функции y=f(x)
существует обратная функция x=g(y),
которая в некоторой точке у0
имеет производную g
'(v0),
отличную от нуля, то в соответствующей
точке x0=g(x0)
функция y=f(x)
имеет производную f
'(x0),
равную
Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0. Покажем,
что
Пусть
Следовательно,
что и требовалось доказать. Эту
формулу можно записать в виде
|

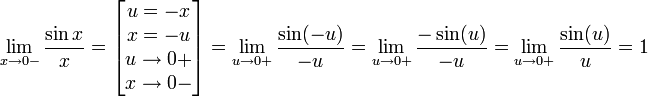
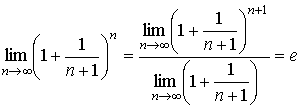
 есть бесконечно малая по сравнению с
функцией
есть бесконечно малая по сравнению с
функцией
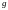 при
при
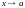 и пишут
и пишут
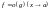 ,
если
,
если
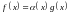 ,
где
,
где
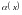 - бесконечно малая функция при
.
- бесконечно малая функция при
.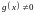 в
в
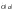 ,
то последнее определение можно записать
как
,
то последнее определение можно записать
как Определение.
Говорят, что функции
Определение.
Говорят, что функции
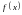 и
и
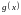 эквивалентны при
и пишут
эквивалентны при
и пишут
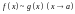 ,
если
,
если
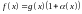 ,
где
,
где
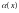 - бесконечно малая функция при
.
- бесконечно малая функция при
.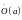 ,
,
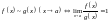
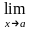 .
.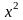 )
- сложная функция.
)
- сложная функция.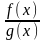 (при
условии g(а)
0) непрерывны в точке а.
(при
условии g(а)
0) непрерывны в точке а.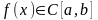 .
Тогда
.
Тогда
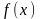 ограничена
на
ограничена
на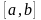 .
.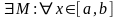
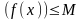 .
.
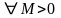
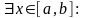
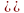 .
Возьмем
.
Возьмем
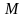 =1,2,3…
=1,2,3…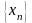 :
: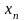
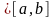
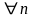
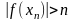

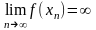 .
.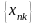 -подпоследовательность
последовательности
:
-подпоследовательность
последовательности
: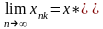 .
.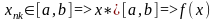 -непрерывна
в точке
-непрерывна
в точке
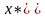 =>
=>
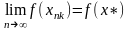 .
.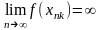 .
Противоречие.
.
Противоречие.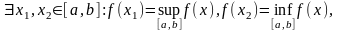
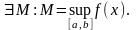 Докажем, что
Докажем, что
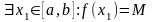 .
Предположим противное, то есть
.
Предположим противное, то есть
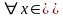
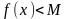 .
Рассмотрим вспомогательную функцию
.
Рассмотрим вспомогательную функцию
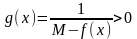 на
.
По 1 теореме Вейерштрасса
на
.
По 1 теореме Вейерштрасса
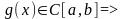 ограничена
на
,
то есть
ограничена
на
,
то есть
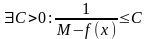
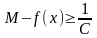
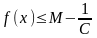
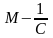 (<
)-
верхняя граница.
(<
)-
верхняя граница.
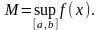 ,
то есть
,
то есть
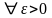
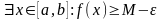 .
Противоречие.
.
Противоречие.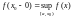 для
x0(a,b],
и
для
x0(a,b],
и
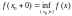 для x0[a,b).
для x0[a,b).
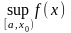 ,
тогда для x[a,x0)
:f(x)A
и для >0
x[a,x0):A-
<f(x).
,
тогда для x[a,x0)
:f(x)A
и для >0
x[a,x0):A-
<f(x).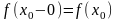 ,
,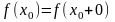 .
.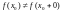 .
Так как функция
возрастает, то это означает, что
.
Так как функция
возрастает, то это означает, что
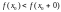 .По
лемме
.По
лемме
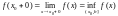 .
.
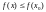 при x
x0,
f(x0)
< f(x0+0)
f(x) при
при x
x0,
f(x0)
< f(x0+0)
f(x) при
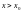 .
Таким образом, значения между f(x0),
f(x0+0)
не достигаются, что противоречит
условию теоремы.
.
Таким образом, значения между f(x0),
f(x0+0)
не достигаются, что противоречит
условию теоремы.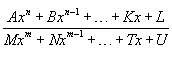 ;
; Обратные
гиперболические функции
Обратные
гиперболические функции
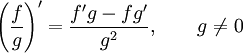 Правило
дифференцирования функции в степени
другой функции:
Правило
дифференцирования функции в степени
другой функции:
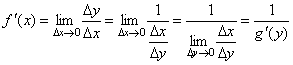 ,
,