Свойства уравнения Шредингера.

Если волновая функция имеет вид

где E=const, - некоторая функция координат, то плотность вероятности обнаружения частицы в любой точке пространства не зависит от времени.

Квантовые состояния, описываемые волновыми функциями рассмотренного вида, называют стационарными состояниями.

Исходя из вероятностного смысла волновой функции, вероятность Р обнаружения частицы в объёме пространства V.

Стационарное уравнение Шредингера.

Для одномерного случая

.

или

или

Задача о стационарных состояниях в квантовой механике.

Частица в одномерной потенциальной яме с бесконечно высокими стенками.

Потенциальная энергия частицы имеет вид:

U(x)=

В области I и III частица находиться не может, так как стенки ямы имеют бесконечную высоту в шкале энергий .

В области II, т.е. в области возможного движения частицы, решение стационарного уравнения Шредингера с учетом конечности, однозначности, непрерывности и нормировки для волновой функции имеет вид:

Выведем это: т.к. непрерывна, то она должна быть равна нулю и на границе ямы.

Уравнение Шредингера для области , гдеU(x) = 0 имеет вид:

то её можно обозначить через квадрат действительного числа

Это уравнение гармонических колебаний.

Решение этого уравнения известно:

А и В произвольные постоянные интегрирования. Определяются из начальных условий: при (sin 0=0; cos 0=1)

где n=1,2,3,…

Значение n=0 исключается, так как в этом случае , частица нигде не находится.

Частица имеет в потенциальной яме дискретный энергетический спектр. Энергия квантована, то есть зависит от квантового числа. n=1 - основное состояние частицы. Все остальные состояния называются возбужденными.

Собственные значения волновой функции

А определяется с помощью условия нормировки:

Рассмотренная задача является моделью потенциального поля атома или молекулы. Изолированный атом является потенциальной ямой, в которой электрон может занимать одно из дискретных энергетических значений. Каждому квантовому состоянию волновой функции соответствует значение полной энергии частицы (квантование энергии).

Частица в прямоугольном трехмерном потенциальном ящике.

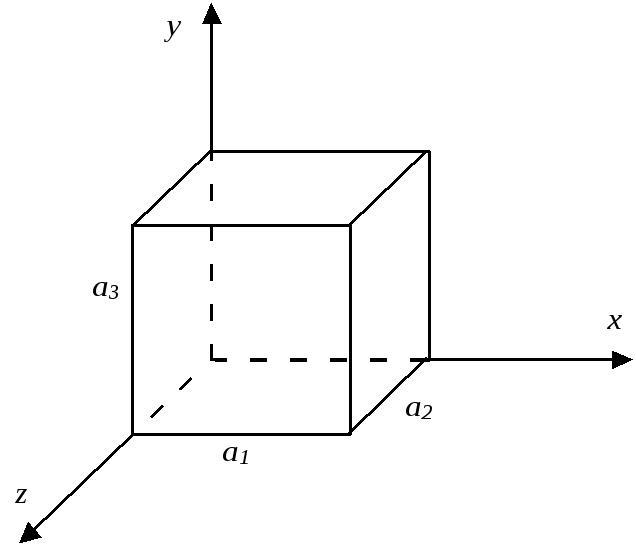
Обозначим G{0<x<,0<y<,0<z<} внутренняя область параллелепипеда. Потенциальная энергия в точке М(х, у,z) имеет вид:

Вне потенциального ящика волновая функция равна нулю.

Внутри потенциального ящика волновая функция может быть найдена как решение стационарного уравнения Шрёдингера:

Это решение имеет вид:

Квантовое состояние частицы, находящейся в потенциальном ящике, определяется тремя квантовыми числами . Каждому квантовому состоянию соответствует определенное значение энергии частицы.

Только при этих значениях полной энергии частицы уравнение Шрёдингера имеет регулярные решения.

Понятие о вырождении энергетических уровней.

Если , то есть для потенциального ящика кубической формы, когда задача обладает пространственной симметрией за счет равноправия всех трех межпространственных направлений, существуют квантовые соотношения (например

), находясь в которых частица имеет одинаковые значения полной

энергии.

Совокупность таких состояний, в которых частица имеет одинаковые значения полной энергии Е, называют вырожденными состояниями, а число состояний, соответствующих данному значению Е, называется кратностью или степенью вырождения.

Например: тогдатак как нельзя подобрать три другие целые числа, сумма квадратов которых равна 3, то этому состоянию (1, 1, 1) соответствует только одно значение энергии.

Но если , то соответствует значение энергии

nx	ny	nz
1	2	3	14
1	3	2	14
2	1	3	14
2	3	1	14
3	2	1	14
3	1	2	14

Этому значению энергии соответствует шесть различных состояний. Такие состояния вырожденные, а число совпадающих уровней энергии называется квантовым весом состояния. В первом случае квантовый вес равен 1, а во втором - 6. Кратность вырождения равна 6.