Корпускулярный механизм передачи энергии

Энергия, переносимая частицами поступает «порциями» и она может быть передана одному электрону, который вылетает из металла. Это объясняет все свойства перечисленные ранее. Эксперимент с фотоэффектом указывает, что свет ведет себя подобно току частиц. Облучая светом объект, бомбардируют и дождем быстрых частиц.

Соотношение справедливо и по отношению к свету (фотонам)для фотонов.

Поток света переносит энергию, а следовательно и связанный с этой энергией импульс: или;

Формула связывает импульс с длиной волны, т.е. имеет место корпускулярно-волновой дуализм, т.е. электрон в фото эмиссии частица, а электрон в атоме водорода – стоячая волна. Частицы имеют двойственную природу.

Это соотношение было установлено в опытах Лебедева П.Н. По определению давления света , гдеE– энергетическая освещенность;

W– объемная плотность энергии излучения;

- коэффициент отражения.

, где;

;; Радиус 1-ой боровской орбиты

1=10^-10м=10^-8см

Длина волны электрона сравнима с размером атома. Если запасенная энергия электронной волнысохраняется, то этостоячая волна. Электрон в атоме водорода – стоячая волна. Электрон в фотоэффекте – частица. Корпускулярно-волновой дуализм.

Энергия в фотоэффекте линейно связана с частотой, должна существоватьпороговая частота.

Диапазон видимого света:

0,75 мкм – 0,4 мкм.

и тогда соответствующая работа выхода:

если, тоили

Соответствующая работа выхода

1 эв=

Соответствующая работа выхода

Соответствующая этой частоте длина волны изучения и называется «красной границей» фотоэффекта.

- максимальная длина волны.

или, где- минимальная частота света, при которой еще возможен фотоэффект.

Квантовое объяснение эффекта Комптона

Э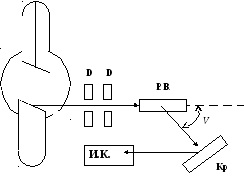ффект можно объяснить, рассматривая рассеяние как процессупругогостолкновения фотонов со свободными электронами. Фотон передает электрону энергию при столкновении:(1) З.С.Э.

З.С.И.

(2), где- энергия рентгеновского фотона, где;

- энергия свободного электрона,- масса покоя электрона,;

- энергия рассеянного рентгеновского фотона;

- энергия электрона после столкновения с фотоном;

- импульс рентгеновского фотона до столкновения, где

- волновой вектор;

- импульс электрона после столкновения с фотоном;

- импульс рентгеновского фотона после столкновения

- волновой вектор.

V- угол рассеяния между векторамии.

З.С.Э. (1)

З.С.И. (2)

Второе уравнение – векторное, его фиксирует . Определяем из этого, равной по величине:

(3) или

(4).

Уравнение (1): (5) возведем в квадрат:

(6).

Вычитая (4) из (6), получим

(7), где.

Простые преобразования в (7):

(8), или

(9).

Определяем :

, где.

Это и есть формула для изменения частоты.

и, тогда

или.

- комптоновская длина волны электрона.

Для V=0,; для,; для,.

Окончательная формула:

.

Чтобы определить, является ли частица, обладающая импульсом P=mVклассической или релятивистской физики, надо сравнить ее импульс с величинойm₀c, называемой комптоновским импульсом, если, то частица классическая!!!

Выводы теории были подтверждены в 1923 г.

Опыты по рассеянию -частиц. Формула Резерфорда. Ядерная модель атома.

Модели атома:

Модель Томсона:в стабильных атомах все заряды неподвижны. У лития положительный заряд равен +3.

Модель атома Резерфорда.

В планетарной модели полная энергия:

Скорость Vиrсвязаны отношением:

.

Центростремительная сила обусловлена кулоновской силой притяжения: .

Если , то электрон будет вращаться вокруг протона с постоянной скоростью по орбите постоянного радиуса.

Но вращающаяся электронно-протонная пара подобна вращающемуся диполю с разнесенными зарядами и представляет собой эффективно излучающую дипольную антенну.

Такой диполь генерирует поперечное электромагнитное поле, излучая свою энергию. При этом E_t, r уменьшаются, система испытывает радиационный коллапс! Который должен произойти за время 10^-8с. Модель несостоятельна.

Чтобы избежать коллапса, была предложена статическая модель атома - модель Томсона или как ее называют "пудинг с изюмом"; размер атома определяется протоном, а заряд распределен по объему атома. Электрон притягивается к протону и коллапсирует в него. В центре протона электрон приходит в состояние покоя. Если несколько электронов, то силы их взаимного отталкивания уравновесятся притяжением к "размазанному" в пространстве положительному заряду. Это модели и нужны эксперименты.

Резерфорд бомбардировал атомы золота "голыми" (без электронов) атомами гелия (- частицами) с энергией 5,5 Мэв.

В двух моделях должен происходить совершенно разный характер рассеяния

Начальная кинетическая энергия частиц больше критического

, где и- число протонов соответственно в

налетающей частице и мишени. Для частиц с такой кинематической энергией в модели Резерфорда происходит в обратном направлении (под углом больше чем 90°), а в модели Томсона только вперед. Для золота соответствующий потенциал равен:

Известно, что атомный радиус поэтому при кинематической энергии

бомбардирующих мишень ионов гелия свыше примерно 3кэв наличие и отсутствие рассеянных в обратном направлении частиц. Выясним, какая из этих моделей является правильной.

Формула Резерфорда:

где b- прицельный параметр.

Резерфорд обнаружил:

1. обратное рассеяние,

2. положительный заряд атома золота сосредоточен в области с размерами порядка