Соотношения неопределенностей.

В классической механике записаны так .

Т.е. на опыте, исходя на основе физических соображений, не можем одновременно получить абсолютно точные значения. Неопределенности обусловлены не совершенством наших измерений, а самой природой материи.

Квантовая механика приводить к неизбежности этих неопределенностей.

Неопределенности или неточности характеризуются квадратным корнем из среднего квадрата отклонения:

Они указывают верхний предел точности, который может быть достигнут при одновременном измерении координат m импульсов; произведение неточностей не может

быть меньше

Свободная частица.

Одна частица, движущаяся в отсутствие действия сил в направлении, которое мы примем за ось X. Т.к. силы отсутствуют, то U=const мы можем принять ее равной нулю. Функция Гамильтона в классической механике состоит из одной кинетической энергии

при выбранной оси координат x: , оператор импульса будет

Оператор Гамильтона:

Уравнение Шредингера

Частные решения этого уравнения, таковы

Эти условия удовлетворяют стандартным условиям конечности m непрерывности во всем пространстве при любых положительных значениях E: E>0.

Спектр собственных значений энергии в данном случае сплошной, в отличие от дискретного спектра.

Движение в центральном поле.

Оператор момента количества движения.

Движение в поле центральных сил. Важную роль играет в квантовой механике оператор момента количества движения.

В декартовых координатах:

Теперь мы должны перейти в этой главе к сферическим координатам:

Напишем полный дифференциал как функцияx, у, z .

.

Переход к сферическим координатам, пологая, что r и V остаются постоянными, а изменяется то

Аналогично выводится

Операторы некоммутирующие операторы, поэтому определить можно одну компоненту, а две другие не определяются.

Оператор квадрата момента количества движения

- оператор Лежандра.

Каждый из операторов коммутирует с оператором .

Оператор квадрата момента импульса имеет общие собственные функции с операторами каждой из его проекций.

Законы сохранения в центрально симметричном поле.

Оператор энергии полярных координатах:

Вводится оператор радиального момента:

Если принять во внимание, что то.

Оператор любой составляющей момента количества движения коммутирует с .

.

Это означает, что численное значение момента количества движения сохраняется во времени. икоммутируют с, следовательно все три оператораимеют общие собственные функции.

А поэтому численное значение момента количества движения, одна из его проекций и энергия могут одновременно определенные значения.

, гдеУ- шаровая функция..

Шаровыми функциями называются шаровые полиномы (одновременные), удовлетворяющие уравнению Лапласа или в декартовых координатах

в раскрытом виде

В сферических координатах

Где lесть квантовое число момента количества движения.

- собственное значение квадрата момента количества движения.

т.е.

тогда момент количества движения принимает собственные значения- собственная функция оператора.

Собственные функции и собственные значения оператора проекции момента количества движения.

- циклическая переменная, то условие однозначности решения:

, это будет только в том случае, если, т.е. при измеренииz-составляющей момента количества движения должны получаться числа, являющиеся целыми кратными.

m– магнитное квантовое число.

- собственная функция.

- собственные значения.

Различным значениям l, l=0,1,2,3,…,(n-1)соответствуют различные состоянияs,p,d,f,…

Состояние	l	m	-функция	L	Lz	Lx	Ly
s	0	0	0	0	0	0	0
p	1	1				Неопр.	Неопр.
p	1	0			0	Неопр.	Неопр.
p	1	-1				Неопр.	Неопр.

Волновые функции нормированы. Для каждого l имеется (2l+1) значений проекции момента импульса на ось z, которые являются целыми кратными .

В теории Бора все три проекции строго определены. На рисунке изображено пространственное квантование в состоянииP(1=1). Оператор имеет в этом состоянии три собственные функции:

.

Всем трем собственным функциям соответствует только одно собственное значение L², равное . Поэтому в состоянииP имеет место трехкратное вырождение. Вследствие вырождения состояние должно описываться линейной комбинацией трех функций .

Все направления равновероятны. Всегда имеется отличная от 0 вероятность найти частицу на сфере с радиусом равным единице .

- элемент поверхности сферы r =1

-функции приведены в таблицах при различных 1 и m.

- нормирующий множитель.

- азимутальная функция, зависит только от азимутального числа .

Эта функция соответствует бегущей по окружности волны и отвечает равномерному вращению электрона вокруг ядра, т.е. волна распространяющаяся в -том направлении.

Из условия нормировки:

Исчез множитель от

- вероятность найти частицу в любом месте сферы между кругами широт от . Так как, площадь сферического пояса между этими кругами.

Вероятность, отнесенная к единице площади сферы,

- эта функция и характеризует распределение частиц на сфере по широте.

1	m
0	0
1

П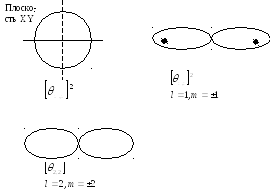олярности диаграммы плотностей вероятностипри. Принято электронное облако (орбиталь) графически изображать контуром, ограничивающим область, в которой вероятность обнаружения электрона составляет 0,9.

В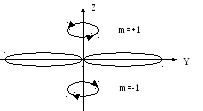состоянииl=0, m=0, E₀=0, сферическая симметрия в распределении заряда электрона

S-состояние; .

Покоящаяся частица может с равной вероятностью в любом месте сферической поверхности радиуса a, т.е. все положения равновероятны. Направление не зависит от угла, классического аналога нет.

P-состояние:

График надо вращать вокруг оси z.

При правое вращение, прилевое вращение (антипараллелен оси z), при m=+1 параллелен.

l=1,m=0 наиболее вероятная орбита та, которая лежит в плоскости, проходящей через ось z.

Во всех случаях наблюдается размытость электронного облака.

Существуют фотографии электронного облака для различных состояний водородоподобного атома.