Оператор квадрата момента импульса

Собственные значения и собственные функции операторов квантовой механики.

Для каждого оператора можно найти функции, которые являются его собственными функциями, т. е. удовлетворяют требованию

(1)

Это главный постулат квантовой механики.

где - действительное число для ирмитовых операторов и называется собственным значением оператора, принадлежащим собственной функции.

В классической механике:

Уравнение для собственных функций и собственных значений оператора энергии будет

где Е - собственное значение оператора энергии; - собственная функция.

В явном виде.

Интегрируя это уравнение в частных производных второго порядка и выбирая те решения, которые удовлетворяют стандартным условиям, получают совокупность собственных функций оператора энергии .

Средние значения физических величин.

В классической механике каждая динамическая величина имеет определённое значение.

В квантовой механике дело обстоит иначе. Например, система находится в состоянии, которое является результатом суперпозиции состояний с собственными значениями.

Если система находится либо в состоянии , либо в состоянии, то соответствующее измерение даст определенное числоилисоответственно. Какое значение будет получатся, когда система находится в состоянии

Здесь в классической физике получилось бы одно строго определённое число.

В квантовой механике получается не одно определённое число, а одно из двух чисел: или , илии никаких других. То или другое значение получается не с достоверностью, а лишь с определённой вероятностью. В квантовой механике нельзя приписать динамической переменной определённого значения, но всегда можно приписать определённую вероятность.

А если известны вероятности, то можно вычислить среднее значение.

Среднее значение координаты х.

Если волновая функция нормирована к единице, то

Учитывая, что оператор координаты “”есть просто умножение на х:

Аналогично

Второй постулат квантовой механики:

где .- обобщённые координаты.

Например: 1) линейного гармонического осциллятора в нормальном состоянии. Нормированная волновая функция этого состояния известна.

где

все интегралы вида вследствие нечётности подынтегральной

функции.

2) Определим P

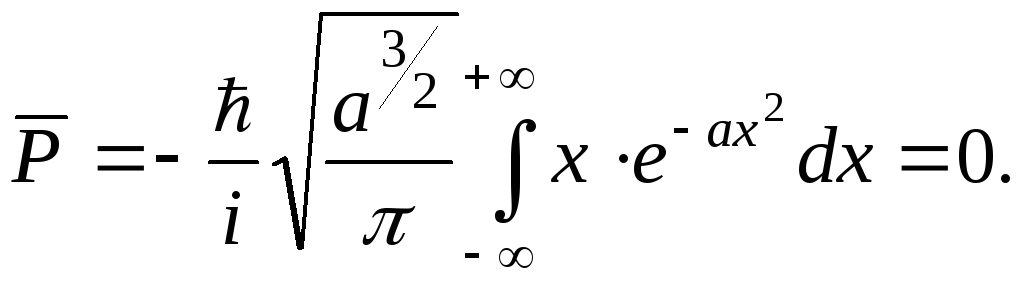
Как и в классической механике, в этом случае равны нулю, что и следовало ожидать из соображений симметрии функцииотносительно х.

3) Вычислим средние значения кинетической и потенциальной энергии:

т. е. средняя потенциальная энергия равна средней кинетической, как и в классической механике.

И как и следовало ожидать, поскольку нулевое состояние есть состояние с определённой энергией.

Условия возможности одновременного измерения разных механических величин.

Согласно одному из основных постулатов квантовой механики, механической величине можно приписывать определённое значение только в том случае, когда это значение является собственным значением - функции, описывающей состояние, в котором находится система.

При каких условиях две или несколько механических могут иметь одновременно определённые значения.

Две механические величины F и G имеют определённые значения, если состояние описывается функцией , являющейся собственной функцией того и другого оператора, т. е.общей собственной функцией.

Например:

Собственные функции этих операторов удовлетворяют уровням.

Где - собственные значения операторов.

Функция равная

удовлетворяет всем этим трем уравнениям, т.е. является общей собственной функцией операторов . Это показывает, что проекции количества движения на все три оси координат могут иметь одновременно определенные значения.

ТЕОРЕМА: Если операторы имеют общие собственные функции, то такие операторы коммутируют.

Пусть общей собственной функцией операторов.

Следовательно,

Обратная теорема: Если операторы коммутируют, то они имеют общие собственные функции.

Динамические переменные имеют общую собственную функцию, следовательно, их операторы коммутируют.

Откуда следует

Аналогично

Координатам соответствующая другой координате составляющая импульса также коммутируют.

Но координата и соответствующая ей составляющая импульса не коммутируют,

т.е.

или

Не могут иметь определенные значения координаты m соответствующие mm составляющие количества движения, либо одна из них имеет определенное значение m тогда другая будет неопределенна.

Составляющие момента импульса не коммутируют: