3 семестp / Лекции / 2(Elektrostatika) / 23
.DOCЛекция 23. Преобразования Фурье
Для
любой
определенной на
справедливо
следующее представление
,
где
- амплитуда, а
- начальная фаза
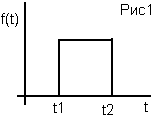
Например функция на рисунке 1 может быть представлена следующим рядом Фурье (рисунок 2)
-
прямое преобразование Фурье в интегральной
форме
Напишем обратное преобразование Фурье в “обычной” интегральной форме
-
cos
составляющая амплитуды частоты
-
sin составляющая
Смысл
обратного преобразования Фурье состоит
в “накоплении”
суммы - если в сигнале (
)
какая-либо частота
“присутствует”
то
сумма будет накапливаться.
Представим преобразования Фурье в комплексном виде:
-
прямое;
- обратное,
где
- оригинал
;
- Фурье
образ.
(замечу,
что здесь нижний предел прямого
преобразования действительно
,
а
не 0)
Краткое пояснение к алгебре комплексных чисел.
-
алгебр.
форма;
- тригонометр.;
- показательная.
;
;
;
.
;
;
;
.
;
;
;
.
Исходя из вышеизложенного можно выполнить следующие преобразования:
Докажем прямое преобразование Фурье
Берем
некоторый ряд Фурье
,
тогда подставив в предыдущую ф-лу
,
(последнее
исходя из
)
- ППФ
доказано.
Докажем обратное преобразование Фурье
,
тк
,
,
тогда
-
ОПФ доказано.
Решение систем диф. ур-ний плоской э/м волны общего вида спектральным методом Фурье
,где
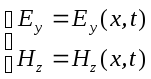- те функции коорд. и времени
Любую
фу-ю можно представить в виде ряда Фурье
представим
и
,
- комплексные амплитуды
-
надо определить в процессе решения.
Подставляя комплексный спектральный интеграл в дифф ур-е волны имеем
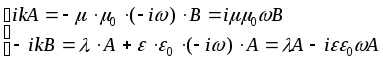
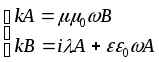
Таким
образои мы получили
.
Разберем далее некоторые важные случаи:
Случай
А
-
- идеальный диэлектрик
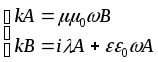
умножим
на
.
тк
- дисперсионное ур-е (примечание:
)
тк
то мы получили решение для электрической и магнитной составляющей поля:
,
где