2. Узагальнений закон Гука.

Для сумісного розгляду теорії напружень та теорії деформацій потрібно встановити залежність між напруженнями та деформаціями. Ця залежність має фізичний характер. Для лінійно - пружних ізотропних тіл фізичні рівняння представляють собою співвідношення узагальненого закону Гука, відомого з курсу “Опір матеріалів”:

(3.21)

де E, G, μ – модуль поздовжньої пружності, модуль пружності при зсуві та коефіцієнт Пуассона, відповідно.

Останні рівняння виражають лінійну залежність між складовими деформації та напруження ми в ізотропному пружному тілі.

При розв’язку задач інколи потрібно мати формули в яких складові напружень виражені через складові деформацій. Для їх отримання складемо ліві та праві частини перших трьох формул (3.21):

Згідно виразів (3.13) та (2.8):

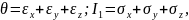
остання формула набуде вигляду:

(3.22)

тобто відносна об’ємна деформація θ пропорційна першому інваріанту напруженого стану І₁. Введемо в розрахунок модуль об’ємного розширення:

отримаємо:

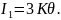(3.23)

Якщо перший інваріант напруженого стану І₁ замінити потроєним середнім напруженням в точці , то замість рівняння (3.23) отримаємо:

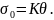(3.24)

Останнє рівняння говорить про те, що середнє напруження в точці пропорційне об’ємній деформації.

Для того щоб виразити складові напруження через складові деформації скористаємося першою формулою закону Гука (3.21), додаючи та віднімаючи в квадратних дужках величину μσ_х:

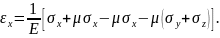
З отриманого виразу виділимо перший інваріант напруженого стану I₁:

(3.25)

Виразимо з формули (3.22) перший інваріант напруженого стану:

(3.26)

Підставимо формулу (3.26) в формулу (3.25):

З останньої формули виразимо σ_х:

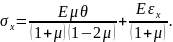(3.27)

Введемо позначення:

та відома з курсу опір матеріалів залежність:

Тоді замість формули (3.27) отримаємо:

Аналогічно останньому виразу, можна отримати формули для обчислення σ_y, σ_z. Після цього є змога записати так званий обернений закон Гука:

(3.28)

В частину формул (3.28) входить коефіцієнт λ, що називають коефіцієнтом Ламе, який характеризує пружні властивості матеріалу.

Складемо між собою праві та ліві частини перших трьох формул (3.28):

Враховуючи, що ліва частина останнього рівняння представляє собою перший інваріант напруженого стану, а права частина в дужках відносну об’ємну деформацію, формула набуде вигляду:

(3.29)

Останнє співвідношення встановлює зв'язок між першими інваріантами напруженого стану та деформованого стану через коефіцієнти Ламе. Замінивши в останньому виразі перший інваріант напруженого стану І₁ на потроєне середнє напруження в точці σ₀, а об’ємну деформацію θ – потроєною усередненою деформацією в точці отримаємо:

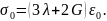(3.30)

Рівняння (3.30) представляє собою ще одну форму закону Гука – середнє напруження в точці прямо пропорційне середньому подовженню в цій точці.