Ф ундаментальная система решений однородной системы линейных уравнений

Фундаментальной системой решений однородного линейного дифференциального уравнения называется упорядоченный набор из n линейно независимых решений уравнения.

Иными словами любые n линейно независимых решений   y₁(x), y₂(x),..., y_n(x) уравнения y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0 образуют фундаментальную систему решений.

 Теорема (о ФСР). Пусть ранг основной матрицы , где — число переменных системы (1), тогда:

• ФСР (1) существует:;

• о 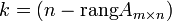на состоит из векторов;

• общее решение системы имеет вид .

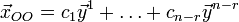Замечание: Если , то ФСР не существует.

Связь решений линейных однородных и неоднородных систем

М етод гаусса решение систем линейных уравнений

Основное соотношение между величинами направленных отрезков на числовой оси

координаты на прямой, плоскости и в пространстве. Формула для вычисления величины направленного отрезка на прямой через координаты его начала и конца

полярные координаты на плоскости и их связь с декартовыми прямоугольными координатами

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — углом и расстоянием. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде расстояний и углов; в более распространенной, декартовой или прямоугольной системе координат, такие отношения можно установить только путем применения тригонометрических уравнений.

Полярная система координат задается лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.^[1]

Определенная таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.

Связь между декартовыми и полярными координатами

Пару полярных координат r и можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса:

в то время как две декартовы координаты x и y могут быть переведены в полярную координату r:

r² = y² + x² (по теореме Пифагора).

Для определения угловой координаты следует принять во внимание два следующие соображения:

• Для r = 0, может быть произвольным действительным числом.

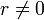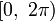• Для , чтобы получить уникальное значение , следует ограничиться интервалом в 2π. Обычно выбирают интервал или .

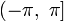Для вычисления в интервале , можно воспользоваться такими уравнениями (arctg обозначает обратную функцию к тангенсу):

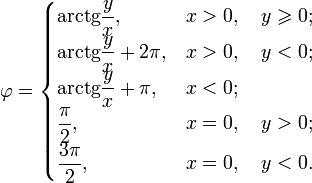
Для вычисления в интервале , можно воспользоваться такими уравнениями:^[14]

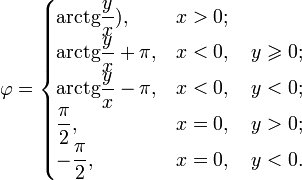
Учитывая, что для вычисления полярного угла не достаточно знать отношение y к x, а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо фукнции atan, определяющей арктангенс числа, еще и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты x.