Определение комплексных чисел и общее правило арифметических действий над ними

z₁ + z₂ = z₂ + z₁.

z₁ + (z₂ + z₃) = (z₁ + z₂) + z₃.

(Д2.47)

Сопряженные комплексные числа. Деление кч

Д ва комплексных числа z=x+iy и z=x-iy отличающиеся

л ишь знаком мнимой части, называются сопряженными

геометрическое изображение комплексных чисел

М одуль и аргумент КЧ

Алгебраическая, тригонометрическая и показательная формы КЧ

Ф ормула Муавра,извлечение корня из КЧ

Формула Муавра для комплексных чисел

, заданная в тригонометрической форме — формула

для любого

Формула Муавра сразу следует из формулы Эйлера и правила для экспонент , верного, если b — целое число. (Если b — не целое, то — многозначная функция переменной a и — одно из её значений.)

Открыта французским математиком Абрахамом де Муавром.

Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа:

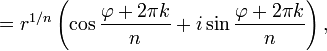
Отметим, что корни n-й степени из комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n-угольника, вписанного в окружность радиуса с центром в точке 0.

Деление многочлена с остатком, теорема Безу

Деление многочлена

Пусть P(x) и Q(x) - заданные многочлены и степень многочлена P(x) больше или равна степени многочлена Q(x). Если оказывается, что многочлен P(x) не делится (нацело) на многочлен Q(x), т.е. не существует многочлена G(x) такого, что P(x)=Q(x)G(x), то вводят операцию деления многочлена с остатком.

Разделить многочлен P(x) на многочлен Q(x) с остатком - это значит найти два многочлена G(x) и R(x) таких, что

P(x)=Q(x)G(x)+R(x),

Причем степень многочлена R(x) меньше степени многочлена Q(x).

Многочлен P(x) называется делимым, Q(x) - делителем, G(x) - частным, R(x) - остатком. При делении многочлена P(x) на многочлен Q(x) многочлены G(x) и R(x) находятся однозначно. Теорема. Для любых двух многочленов P(x) и Q(x) ╪ 0 частное и остаток от деления P(x) на Q(x) существуют и единственны.

Т. Безу. Остатком при делении многочлена f(x) из на линейный многочлен (x-c) является константа f(c). Док-во: При делении f(x) на (x-c) получим: f(x)=q(x)(x-c)+r. Полагая x=c получим: f(с)=q(с)(с-c)+r=r.

Схема Горнера  

 Если то при делении f(x) на g(x) частное q(x) имеет вид

где Остаток r находится по формуле

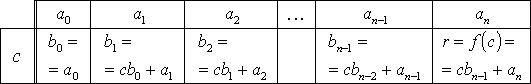a[0]=q[0] a[1]=q[1]-q[0]c a[2]=q[2]-q[1]c ... a[n-1]=q[n-1]-q[n-2]c a[n]=r-q[n-1]c откуда: q[0]=a[0] q[1]=a[1]+q[0]c q[2]=a[2]+q[1]c ... q[n-1]=a[n-1]+q[n-2]c r=a[n]+q[n-1]c.

Основная теорема Алгебры. Разложение на множители многочлена с компл и действ коэфф

Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел. или

Поле комплексных чисел алгебраически замкнуто.

  Разложение многочлена степени n на множители      Многочлен f(x) с комплексными коэффициентами

Здесь - различные корни многочлена кратностей соответственно

Многочлен f(x) с действительными коэффициентами

Здесь - различные действительные корни многочлена, кратностей соответственно - различные пары действительных чисел, удовлетворяющих неравенствам (каждый множитель можно представить в виде где - пара сопряженных комплексных корней кратности ).

Признак взаимно простых многочленов

Для того, чтобы многочлены f(x) и g(x) из F[x] были взаимно простыми, необходимо и достаточно, чтобы в F[x] существовали такие u(x) и v(x), что u(x)f(x)+v(x)g(x)=1. Док-во: - Необходимость: очевидно. - Достаточность: Пусть d(x) - НОД многочленов f(x) и g(x). Значит каждое из слагаемых левой части делится на d(x). А значит и правая часть делится на d(x). Следовательно d(x) - ненулевая константа.

Рациональные дроби и разложение их на простейшие методом неопределённых коэффициентов

Рациональная дробь - это число, представленное в виде дроби, например a / b, где a - числитель, b - знаменатель. A и B могут представлять собой целые числа, а также переменные.

Классическим примером применения метода неопределённых коэффициентов является разложение правильной рациональной дроби в комплексной или вещественной области на элементарные дроби.

Пусть p(z) и q(z) — многочлены с комплексными коэффициентами, причём степень многочлена p(z) меньше степени многочлена q(z), коэффициент при старшем члене многочлена q(z) равен 1, z_i ― корни многочлена q(z) с кратностями α_i, следовательно,

Функция p / q представима, и притом единственным образом, в виде суммы элементарных дробей

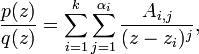
где A_i,j ― неизвестные пока комплексные числа (их число равно степени q). Для их отыскания обе части равенства приводят к общему знаменателю. После его отбрасывания и приведения в правой части подобных членов получается равенство, которое сводится к системе линейных уравнений относительно A_i,j.

Примечание. Нахождение неизвестных можно упростить, если q(z) имеет некратные корни z_j. После умножения на z − z_j последнего равенства и подстановки z = z_j непосредственно получаем значение соответствующего коэффициента .

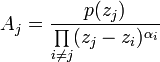Матрицы и действия над ними

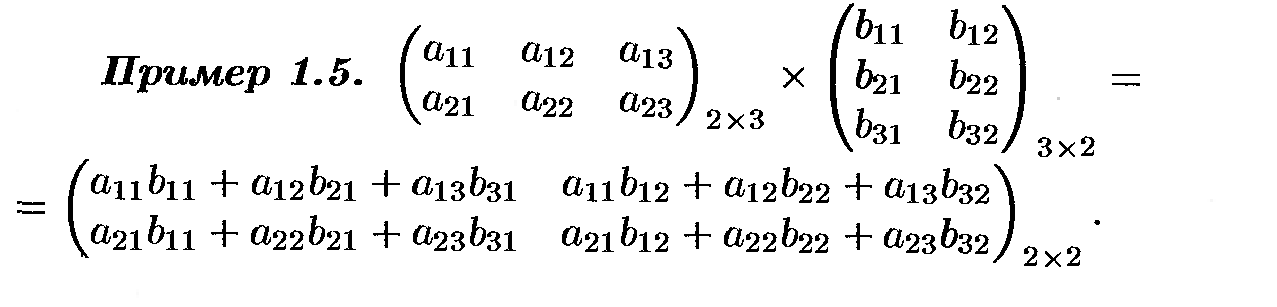
О пределители 2, 3 и n-го порядка

М инором M_ij элемента a_ij (i,j=1,n) называется определитель (n-1)-го порядка, полученный из определителя n-го порядка, вычерчиванием i-й строки и j-го столбца. Алгебраическое дополнение Aij элемента Aij определяется равенством

A_ij=(-1)^i+j M_ij

Для произвольного натурального числа (теорема Лапласа, разложение по i-строке)

Пример Для определителя III-го порядка (при i = 1):

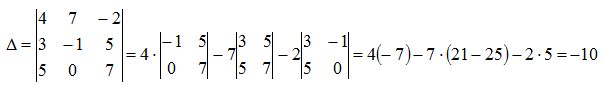
для определителя IV-го порядка:

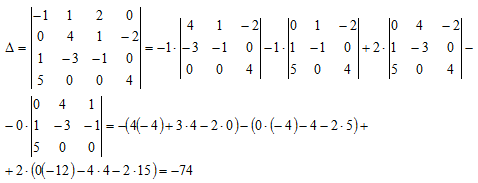
С войства определителей

Разложение определителя по строке или столбцу

  По элементам i-й строки:

      По элементам j-го столбца:

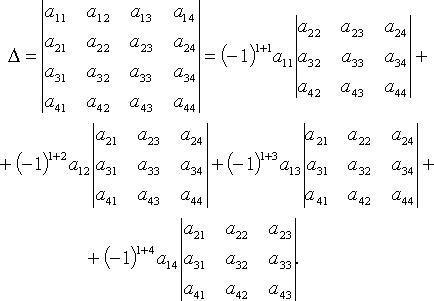      Например, при n = 4 разложение по первой строке

Определитель произведения матриц

О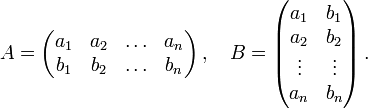 пределитель матрицы равен нулю, если , и равен сумме попарных произведений соответствующих друг другу миноров порядка , если (сумма берется по всем наборам столбцов матрицы и строк матрицы с возрастающими номерами ).

Пусть

Т огда

и соответствующие миноры имеют вид

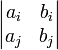
при всех i < j, принимающих значения от 1 до n.

Ф ормула Бине — Коши в этом случае дает равенство

и з которого (в случае, когда все a_i и b_i являются вещественными числами) вытекает неравенство Коши — Буняковского:

Формула Крамера для решения системы линейных уравнений

Обратная матрица и ее вычисление

Свойства обратной матрицы и новый вывод формул Крамера

1. Определитель обратной матрицы обратно пропорционален определителю начальной матрицы

                                                        .                                       (4.1.1)

Д о к а з а т е л ь с т в о :

         А^-1А = E, следовательно, , а отсюда следует (4.1.1).

         2. Обратная матрица произведения двух матриц равна произведению обратных матриц сомножителей, взятых в обратном порядке

                                                        (АВ)^-1 = В^-1А^-1.                                                           (4.1.2)

Д о к а з а т е л ь с т в о :

АВ(В^-1А^-1) = А(ВВ^-1)А^-1 = АЕА^-1 = АА = Е

         и

В^-1А^-1(АВ) = В^-1(А^-1А)В = В^-1ЕВ = В^-1В = Е.

 

Следовательно, по определению (2.1)    В^-1А^-1 - обратная матрица для АВ.

 

         3. Транспонированная обратная матрица равна обратной транспонированной матрице

                                               (А^-1)^ = (А^)^-1.                                                   (4.1.3)

 

Д о к а з а т е л ь с т в о :

         По определению (2.1) А^-1А = Е, тогда

(А^-1А)^ = А^(А^-1)^ =Е^ = Е.

Умножим это равенство на (А^/)^-1:

(А^)^-1А^(А^-1)^ = (А^)^-1Е,

         следовательно,

(А^-1)^ = (А^)^-1.