1. Основные понятия и законы динамики

Динамикой называется раздел теоретической механики в котором изучается движение материальных объектов с учетом причин вызывающих это движение. Первый з-н Ньютона(закон инерции), второй з-н Ньютона(F=ma), Третий з-н Ньютона(з-н равенства действия и противодействия F1=-F2), Четвертый з-н (з-н независимости действия сил)

2 Диф. Ур-я движения своб. Т. В вектор. Форме и проекциях на декарт. И естественные оси коорд.

m(d^2r/dt^2)=F(r,r^.,t)- векторная форма

m(d^2s/dt^2)=F; m(v^2/p)=Fn; Fb=0 естественные оси

3 матем. Подстановка и решение двух основных задач динамики точки

Первая задача динамики.

По заданному движению точки определить силу.

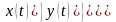- уравнения движения точки

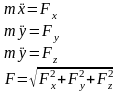
Решение второй (основной) задачи динамики

Эта задача состоит в том, чтобы, зная действующую силу F, найти закон движения точки, т. е. кинематические уравнения (6). Сила F может вообще зависеть от времени, от положения точки в пространстве и от скорости ее движения, т. е.  . Поэтому дифференциальные уравнения (5) будут в общем случае иметь следующий вид:

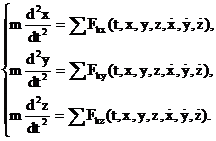                                              (7)

 

Нахождение закона движения данной точки сводится к интегрированию системы (7), т. е. системы трех совместных дифференциальных уравнений второго порядка, в которых неизвестными функциями являются координаты движущейся точки х, у, z, а аргументом - время t. Проинтегрировав эту систему дифференциальных уравнений, получим х, у, z в функциях времени и шести произвольных постоянных, т. е. найдем общее решение (общие интегралы) системы (7) в виде

 

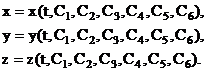                                             (8)

 

Наличие в правых частях уравнений (8) произвольных постоянных указывает на то, что под действием данной силы точка может совер­шать не какое-то вполне определенное движение, а целый класс движений, имеющих разные законы при разных значениях постоянных C_i, i=1..6.

Физически этот результат объясняется тем, что точка, на кото­рую начинает действовать некоторая сила, будет двигаться по-раз­ному в зависимости от так называемых начальных условий, т. е. от начального положения и начальной скорости этой точки. Напри­мер, движение свободной материальной точки под действием силы тяжести может быть прямолинейным или криволинейным в зависи­мости от направления ее начальной скорости.

Чтобы сделать соответствующую задачу динамики определенной, надо кроме действующих сил задать начальные условия, т. е. для некоторого момента времени t = t₀ (начальный момент) задать:

начальное  положение точки    

и  начальную  скорость    точки     

4 прямолинейное движение. Диф. Уравнение прям. Движения

Свободная мат. Точка движется по прямолинейной траектории тогда и только тогда, когда сила, приложенная к точке имеет постоянное направление и начальная скорость паралельна этому направлению. (m(d^2x/dt^2)=Fx(t,x,x^.)- диф. Ур. Прямолин. Движ.

7 дв. Несвободной мат. Точки. Динамика относит. Движения т. Инерциальные и неинерцаоьные сис-мы отсчета. Переносная и кариолисова силы инерции. Диф. Ур-я относит. Движ. Т. Примеры частных случаев относит. движ. Точки

Несвободной материальной точкой называется точка, свобода движения которой ограничена.

Тела, ограничивающие свободу движения точки, называются связями.

Пусть связь представляет собой поверхность какого-либо тела, по которой движется точка.  Тогда координаты точки должны удовлетворять уравнению этой поверхности,  которое называется уравнением связи.

m(d^2/dt^2)=F+N

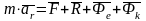-диф ур-е относит. Движ.

8 мех. Сис-ма. Классификация сил действ. На сис-му. Св-ва внутр. Сил. Диф ур-я движ. Мех. Сис-мы

Мех. Сис-ма-это совокупность взаимодействующих между собой м.т.

Все силы можно разделить на заданные силы и реакции связи, с другой стороны силы можно классифицировать по иному признаку внутр. И внешние силы

1 св-во главн вектор всех внутр сил мех сис-мы равен нулю

2 св-во гл момент всех внутр сил относит произвольного центра равен нулю

- диф. Ур-е

9 центр масс сис-мы. Моменты инерции теорема гюйгенса. Связь между полярным и осевыми моментами инерции. Гл оси инерции тела. Примеры вычисл моментов инерции

Ц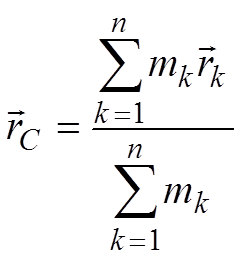 ентром масс мех сис-мы наз геометрическая точка с, положение которой определяется радиус-вектором r по формуле: центр масс сис-мы – это такая т относит которой статистический момент массы равен 0

Момент инерции — скалярная физическая величина, мера инерции тела во вращательном движении вокруг оси

М омент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

I_xz=I_yz=0 z-гл ось инерции тела

10 кол-во движ т и мех сис-мы. Элементарный и полный импульс силы

Кол-вом движения м т q наз векторная величина равная произведению массы на ее скорость

q=mv

Q=MVc (мех сис-мы)

ds=Fdt (элемент. Импульс)

S=(интеграл от 0 до t)Fdt-полный импульс

11 теорема о колич движ точки и мех сис-мы