Вариант 1

1. Определение а) достоверного и б) невозможного события. Какие события называются в) несовместными г) совместными. Пусть брошена игральная кость. События , . характеризовать а) , б) . Совместны или нет в) события A, B, г) , .

Теория

а) {А – достоверное событие} ↔ {А = } ↔ { А – обязательно наступит в результате с Э}

б) { А – невозможное событие} ↔ {А = Ø} ↔ { А – заведомо не наступит в результате с Э}

в) { А и В - несовместные} ↔ { А·B =Ø}

г) { А и В - совместные} ↔ { А·B ≠ Ø}

Практика

_{а) = {1,2,3,4,5,6} – достоверное}

_{б) = Ø – невозможное}

_в) A, B – совместные и образуют полную группу

г) , - совместные и равные.

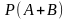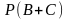2. Записать формулу для а) P(Ø) б) в) г) P(A+B+C). Если , , чему равно б) , в) г) .

ОТВЕТ

а) P(Ø)=0

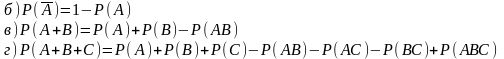
Практика

3. Определение а) математического ожидания, б) дисперсии, в) среднего квадратичного отклонения для дискретной случайной величины. Выписать г) формулу используют для вычисления дисперсии. Пусть 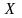имеет распределение:

Найти а) б) , в) .

Теория

а) M(x) = _k ∙ p_k =Σ x_n ∙ p ( x = x_n )

б) D (x) = M((x – M (x))²)

в) σ (x) =

Практика

а) M(x) = 1 ∙ 0,25 + 2 ∙ 0,5 + 3 ∙ 0,25 = 2

б) D (x) =

в) σ (x) =

4. Определение а) математического ожидания для непрерывной случайной величины. Чему равно мат. ожидания от а) линейной комбинации с.в. б) произведения с.в. Пусть имеет плотность распределения . Вычислить а) , б)

ОТВЕТ

а) - математ. ожидание

б) X₁и X₂ – независимые случайные величины

Практика

Вариант 2

1. Формула числа сочетаний а) без повторений б) с повторениями. Сколькими способами а) можно выбрать из коллектива в 8 человек 3-х дежурных б) составить из 3 видов цветов букет из 5 цветов.

Теория

а) = =

б) = =

Практика

а) n = 8

k = 3 → сочетание без повторения → = = = 56

б) n = 3

k = 5 → сочетание с повторением → = = = 21

2. Определение а) классического случайного эксперимента. б) Формула вычисления вероятности в классическом случайном эксперименте. Пусть наудачу выбрасывается карточка с двузначным числом, событие A – выпало 11, B - цифры в числе разные. Вычислить а) P(A) б) P(B) в) Р(A+B).

ОТВЕТ

a)Пусть

1. A -сэ - Ω = {w_i}1<|Ω| =n<∞

2.w_i – равновозможны

Тогда

1. (A ,Ω) - классический случайный эксперимент

б) P(A)=|A|/|Ω|=m/n , Aϲ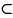 Ω - Формула вычисления вероятности случайных событий

(m- число благоприятных ЭИ, n–общее число исходов)

Практика

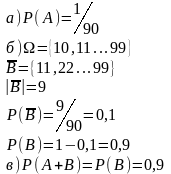
3. Определение а) схемы Бернулли. Записать б) формулу Бернулли. В тесте четыре вопроса, и в каждом вопросе 3 варианта ответа Какова вероятность а) на удачу правильно ответить на 2 вопроса б) более чем на 1 вопрос?

Теория

а) {Схема Бернули – последовательность n независимых в совокупности элементов(испытаний), в каждом из которых возможно 2 исхода: успех или неудача}

б) P(B_(min)) = =

Практика

4. Дать а) определение непрерывной случайной величины б) плотности распределения. Записать в) 3 свойства плотности. Пусть - функция распределения случайной величины X. Найти а) б) в) плотность распределения.

ОТВЕТ

а) Х – непрерывная случайная величина

б)при этом функция f(x) удовлетворяющая равенству ) – плотность распределения C.В.Х

в)свойства

Практика